一种描述高温材料蠕变变形三阶段的方法及模型与流程

本发明涉及一种能够完整描述高温材料蠕变变形三阶段的方法及模型，属于高温结构强度技术领域。

背景技术：

蠕变通常是指在温度、载荷/应力不变的条件下，变形随时间的增加而增大的现象。其主要特点在于当结构的温度达到一定时，即使其内部的应力远小于材料的屈服强度仍然能产生明显的蠕变。航空发动机热端部件特别是转动件承受着高温和大应力，在使用中会发生明显的蠕变现象。

目前常用的蠕变模型有时间硬化模型和应变硬化模型等，但这类模型只能描述蠕变第一阶段或者前两个阶段。然而，在实际的蠕变问题中第三阶段的蠕变变形占据了整个寿命期内蠕变变形的70％以上，在应力水平较小时甚至占到总变形的80％以上，且第三阶段寿命占到总寿命的50％左右，因此，对蠕变第三阶段的变形描述是分析高温结构/材料失效过程、预测构件变形或寿命的基础。1985年evans和wilshire在其著作中提出一种能描述完整的蠕变变形的模型——θ映射法，虽然θ映射法可以模拟蠕变变形的3个阶段，但其模型中的参数并不具有很好的物理基础，此外，在2015年由王延荣等人提出的归一化参数蠕变模型与θ映射法类似，均能描述蠕变三个阶段，但是蠕变参数缺少物理意义。而对基于纯蠕变物理过程建立的模型而言，确定参数的方法太过繁琐，且计算过程相当复杂，不利于工程应用。因此，有必要发展一种既能反应蠕变物理过程又能够更加便于应用的蠕变模型。

技术实现要素：

为发展一种既能更好反应蠕变物理过程又能便于工程应用的蠕变模型，解决目前商用有限元软件中自带模型不能描述蠕变三阶段的问题，使得模型既能描述蠕变变形整体过程又能反应蠕变的微观物理过程，本发明的目的是提供一种描述高温材料蠕变变形三阶段的方法及模型。

为实现上述目的，本发明采用的技术方案为：

一种描述高温材料蠕变变形三阶段的方法，包括以下步骤：

(1)通过试验获得材料的工程蠕变变形-时间曲线，并将其转换为真实蠕变应变-时间曲线；

(2)将步骤(1)得到的真实蠕变应变-时间曲线进行归一化；

(3)将蠕变模型中的参数k、η、α表示为应力和温度的函数；其中，上式中：ε^c为蠕变应变，σ为应力，t、tf分别为蠕变时间和材料在指定温度、应力下的断裂寿命；

(4)利用试验数据拟合蠕变模型参数；

(5)将蠕变模型嵌入有限元软件，实现对实际结构的蠕变分析。

所述步骤(1)中，利用体积不变假设，将试验获得的工程应力和工程蠕变应变转换为真实应力和真实蠕变应变，并与试验时间一起构成蠕变模型参数拟合的初始数据；真实应力和真实蠕变应变转换公式为：

式中：σt、σe分别为真实蠕变应变、真实应力、工程蠕变应变以及工程应力，εe,εp分别为工程弹性应变和工程塑性应变。

所述步骤(2)中，分别运用各自试验载荷、温度下的断裂寿命将蠕变试验时间除以断裂寿命，获得归一化时间、真实应力以及真实蠕变应变三列数据，作为模型参数拟合的输入数据。

所述步骤(3)中，参数k、η、α的温度和应力函数表达式为：

k＝c1+c2σ+c3t+c4σt，式中σ为施加应力，t为试验温度，c1-c4为试验拟合常数；

η＝c5+c6σ+c7t+c8σt，式中σ为施加应力，t为试验温度，c5-c8为试验拟合常数；

α＝c9+c10σ+c11t+c12σt，式中σ为施加应力，t为试验温度，c9-c12为试验拟合常数；

当各试验条件下的温度相同时上述表达式简化为k＝c1+c2σ、η＝c3+c4σ、α＝c5+c6σ。

所述步骤(4)中，利用1stopt软件中的参数拟合功能，采用麦夸特法和通用全局优化法，拟合得到参数ci的值，下标i为1至12，当各试验温度相同时得到简化后的参数ci的值，下标i为1至6。

所述步骤(5)中，编写有限元蠕变子程序usercreep时需要提供蠕变应变增量delcr、蠕变应变增量对等效应力的导数dcrda(1)和蠕变应变增量对蠕变应变的导数dcrda(2)；

若各试验温度相同，则其表达式分别为：

delcr＝((σ·exp(-k/η·t/tf)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)-(σ·exp(-k/η·t/tf)·k·(exp((α+k/η)·t/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α)))·δt，

dcrda(1)＝((exp(-k/η·t/tf)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)+(σ·exp(-k/η·t/tf)·((c6·(t/tf)^(α-1))/tf+(exp((t·(α+k/η))/tf)·(c6+c2/η-(c4·k)/(η)^2))/tf-(c6·(t/tf)^(1/α))/(tf·(α)^2)+(c6·log(t/tf)·(t/tf)^(α-1)·α)/tf+(t·exp((t·(α+k/η))/tf)·(α+k/η)·(c6+c2/η-(c4·k)/(η)^2))/tf^2-(c6·log(t/tf)·(t/tf)^(1/α)·(1/α+1))/(tf·(α)^2)))/(k+η·α)-(σ·exp(-(t·k)/(tf·η))·((c2·t)/(tf·η)-(c4·t·k)/(tf·(η)^2))·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)-(σ·exp(-(t·k)/(tf·η))·(c2+c6·η+c4·α)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)^2-(exp(-(t·k)/(tf·η))·k·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α))-(c2·σ·exp(-(t·k)/(tf·η))·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α))-(σ·exp(-(t·k)/(tf·η))·k·(c6·log(t/tf)·(t/tf)^α+(t·exp((t·(α+k/η))/tf)·(c6+c2/η-(c4·k)/(η)^2))/tf-(c6·log(t/tf)·(t/tf)^(1/α+1))/(α)^2))/(tf·η·(k+η·α))+(σ·exp(-k/η·t/tf)·k·(c2+c6·η+c4·α)·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α)^2)+(c4·σ·exp(-k/η·t/tf)·a1·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·(η)^2·(k+η·α))+(σ·exp(-(t·k)/(tf·η))·((c2·t)/(tf·η)-(c4·t·k)/(tf·(η)^2))·k·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α)))·δt，

dcrda(2)＝((σ·exp(-(t·k)/(tf·η))·((exp((t·(α+k/η))/tf)·(α+k/η)^2)/tf^2+((t/tf)^(1/α-1)·(1/α+1))/(tf^2·α)+((t/tf)^(α-2)·α·(α-1))/tf^2))/(k+η·α)+(σ·exp(-(t·k)/(tf·η))·k^2·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf^2·η^2·(k+η·α))-(2·σ·exp(-(t·k)/(tf·η))·k·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(tf·η·(k+η·α)))·(1/((σ·exp(-k/η·t/tf)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)-(σ·exp(-k/η·t/tf)·k·(exp((α+k/η)·t/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α))))·δt

上式中，δt为软件计算中的时间增量。

一种描述高温材料蠕变变形三阶段的模型，该模型的表达式为：

式中：ε^c为蠕变应变，σ为应力，t、tf分别为蠕变时间和材料在指定温度、应力下的断裂寿命，k、η、α均表示为应力和温度的函数，为反应材料内部蠕变过程中位错变化的参数。

有益效果：本发明提出的方法及模型既反应了由材料内部位错变化引起的蠕变第一阶段和第二阶段的变形特征，又包含了蠕变空洞等损伤引起的第三阶段应变速率随时间增加迅速增大的现象，因此能够更加准确的描述材料的蠕变变形全过程。通过编写有限元子程序，可以将本发明的模型应用于实际结构的蠕变分析中。

附图说明

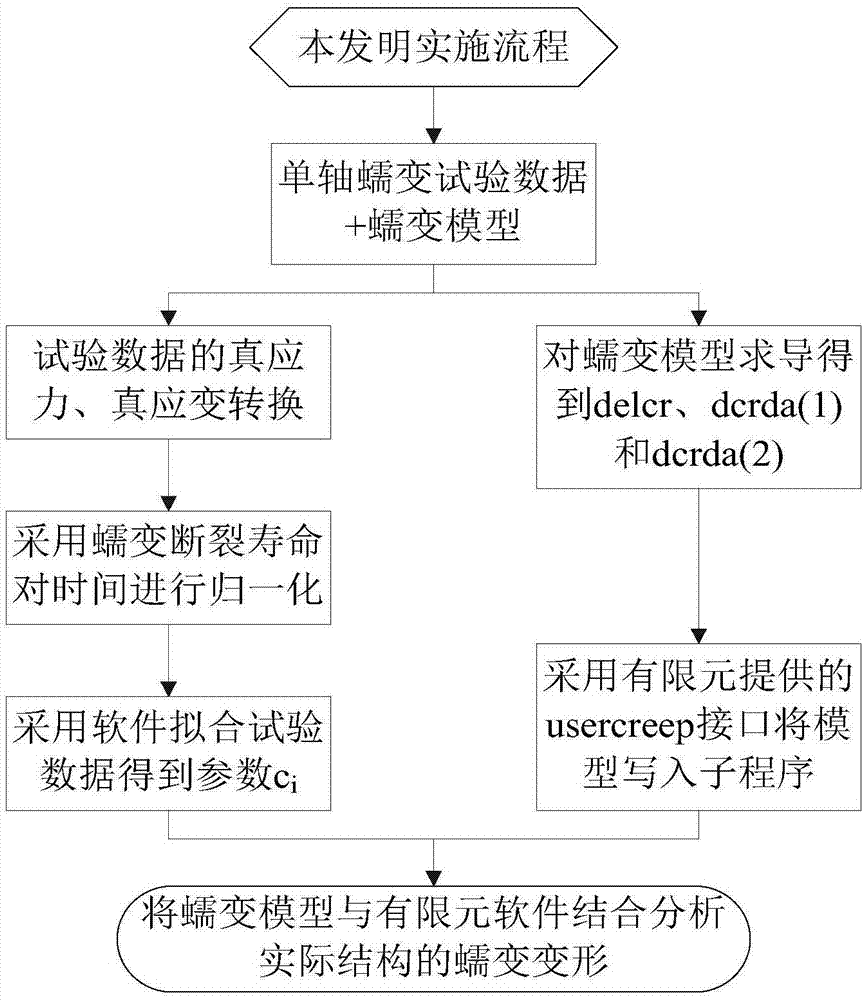
图1为本发明的实施流程图；

图2为典型蠕变曲线及其三个阶段示意图；

图3为tc11材料500℃下4种应力条件的工程蠕变应变图；

图4为tc11材料500℃下4种应力条件的真实蠕变应变图；

图5为tc11材料500℃下4种应力条件归一化时间的真实蠕变应变图；

图6为tc11材料500℃下4种应力条件试验的归一化蠕变曲线与模型拟合曲线对比图；

图7为tc11材料500℃下4种应力条件试验的蠕变曲线与模型拟合曲线对比图。

具体实施方式

本发明提供一种描述高温材料蠕变变形三阶段的方法及模型，包括能够反应材料内部因应变硬化而导致蠕变速率逐渐下降的蠕变第一阶段、硬化过程与恢复过程达到平衡而产生的蠕变速率趋于恒定的蠕变第二阶段以及因材料内部产生空洞和裂纹而导致蠕变速率快速增大的蠕变第三阶段。并且通过编写有限元软件ansys的usercreep子程序，将该方法应用于实际结构的蠕变变形分析中。蠕变应变的表达式为：

式中：ε^c为蠕变应变，σ为应力，t、tf分别为蠕变时间和材料在指定温度、应力下的断裂寿命，k、η、α均表示为应力和温度的函数，该模型的主要特点在于：k、η、α为反应材料内部蠕变过程中位错变化的参数，能够很好的描述蠕变的第一阶段和第二阶段。此外，通过断裂寿命对时间进行归一化，引入第三阶段的蠕变损伤来描述第三阶段的变形规律，即式(1)中等号右边中括号里的第二项。同时式(1)中等号右边中括号里的第三项对蠕变变形的第一阶段进行修正，最终达到能够更好描述材料蠕变变形规律的目的。

下面结合实际应用实例和附图对本发明作更进一步的说明：

本发明涉及的一种描述高温材料蠕变变形三阶段的方法，其实施流程如附图1所示，典型的材料蠕变曲线如附图2所示，其在tc11钛合金材料500℃下的蠕变变形分析中的运用包括以下步骤：

(1)通过试验获得tc11材料500℃下的工程蠕变应变-时间曲线，如附图3所示，将其转换为真实蠕变应变-时间曲线，如附图4所示；

光滑试件蠕变试验获得材料的工程蠕变-时间曲线(ε^c-t)，由如下变换公式转化为真实蠕变-时间曲线和真实应力；

式中：σt、σe分别为真实蠕变应变、真实应力、工程蠕变应变以及工程应力，εe,εp分别为工程弹性应变和工程塑性应变；

(2)将tc11材料500℃下的真实蠕变应变-时间曲线进行归一化：

分别运用各自试验载荷、温度下的断裂寿命tf将时间进行归一化，tc11材料在500℃、4种工程应力537mpa、558mpa、580mpa和590mpa作用下的断裂寿命tf分别为645.256h、392.444h、313.728h和215.203h，由此获得归一化时间、真实应力以及真实蠕变应变三列数据，作为模型参数拟合的输入数据，归一化时间的真实蠕变应变曲线如附图5所示；

(3)将参数k、η、α表示为应力和温度的函数；

参数k、η、α的温度和应力函数表达式为：

k＝c1+c2σ+c3t+c4σt，式中σ为施加应力，t为试验温度，c1-c4为试验拟合常数；

η＝c5+c6σ+c7t+c8σt，式中σ为施加应力，t为试验温度，c5-c8为试验拟合常数；

α＝c9+c10σ+c11t+c12σt，式中σ为施加应力，t为试验温度，c9-c12为试验拟合常数；

当各试验条件下的温度相同时上述表达式简化为k＝c1+c2σ、η＝c3+c4σ、α＝c5+c6σ。

(4)利用试验数据拟合蠕变模型参数，拟合结果与试验数据对比如附图6和图7所示；

利用1stopt软件中的参数拟合功能，采用麦夸特法+通用全局优化法，拟合得到参数ci的值，下标i为1至12，当各试验温度相同时可得到简化后的参数ci的值，下标i为1至6，拟合tc11材料在500℃、5种应力下的蠕变试验数据得到的参数c1～c6分别为：

c1＝267782.6665,

c2＝-349.6828，

c3＝48451.6357，

c4＝-175.1019，

c5＝0.55695，

c6＝-0.00044296。

(5)将该模型嵌入有限元软件，实现对实际结构的蠕变分析：

编写有限元蠕变子程序usercreep时需要提供蠕变应变增量delcr、蠕变应变增量对等效应力的导数dcrda(1)和蠕变应变增量对蠕变应变的导数dcrda(2)；

以各试验温度相同的条件为例，其表达式分别为：

delcr＝((σ·exp(-k/η·t/tf)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)-(σ·exp(-k/η·t/tf)·k·(exp((α+k/η)·t/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α)))·δt，

dcrda(1)＝((exp(-k/η·t/tf)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)+(σ·exp(-k/η·t/tf)·((c6·(t/tf)^(α-1))/tf+(exp((t·(α+k/η))/tf)·(c6+c2/η-(c4·k)/(η)^2))/tf-(c6·(t/tf)^(1/α))/(tf·(α)^2)+(c6·log(t/tf)·(t/tf)^(α-1)·α)/tf+(t·exp((t·(α+k/η))/tf)·(α+k/η)·(c6+c2/η-(c4·k)/(η)^2))/tf^2-(c6·log(t/tf)·(t/tf)^(1/α)·(1/α+1))/(tf·(α)^2)))/(k+η·α)-(σ·exp(-(t·k)/(tf·η))·((c2·t)/(tf·η)-(c4·t·k)/(tf·(η)^2))·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)-(σ·exp(-(t·k)/(tf·η))·(c2+c6·η+c4·α)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)^2-(exp(-(t·k)/(tf·η))·k·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α))-(c2·σ·exp(-(t·k)/(tf·η))·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α))-(σ·exp(-(t·k)/(tf·η))·k·(c6·log(t/tf)·(t/tf)^α+(t·exp((t·(α+k/η))/tf)·(c6+c2/η-(c4·k)/(η)^2))/tf-(c6·log(t/tf)·(t/tf)^(1/α+1))/(α)^2))/(tf·η·(k+η·α))+(σ·exp(-k/η·t/tf)·k·(c2+c6·η+c4·α)·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α)^2)+(c4·σ·exp(-k/η·t/tf)·a1·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·(η)^2·(k+η·α))+(σ·exp(-(t·k)/(tf·η))·((c2·t)/(tf·η)-(c4·t·k)/(tf·(η)^2))·k·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α)))·δt，

dcrda(2)＝((σ·exp(-(t·k)/(tf·η))·((exp((t·(α+k/η))/tf)·(α+k/η)^2)/tf^2+((t/tf)^(1/α-1)·(1/α+1))/(tf^2·α)+((t/tf)^(α-2)·α·(α-1))/tf^2))/(k+η·α)+(σ·exp(-(t·k)/(tf·η))·k^2·(exp((t·(α+k/η))/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf^2·η^2·(k+η·α))-(2·σ·exp(-(t·k)/(tf·η))·k·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(tf·η·(k+η·α)))·(1/((σ·exp(-k/η·t/tf)·(((t/tf)^(α-1)·α)/tf+((t/tf)^(1/α)·(1/α+1))/tf+(exp((t·(α+k/η))/tf)·(α+k/η))/tf))/(k+η·α)-(σ·exp(-k/η·t/tf)·k·(exp((α+k/η)·t/tf)+(t/tf)^(1/α+1)+(t/tf)^α-1))/(tf·η·(k+η·α))))·δt。

上式中，δt为软件计算中的时间增量。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。