电力系统PQ法潮流中随机非零元素因子表的形成及应用的制作方法

本发明属于电力系统分析计算领域，涉及一种电力系统pq法潮流中随机非零元素因子表的形成及应用。

背景技术：

潮流计算是电力系统分析中最基本的计算，也是网损计算、静态安全分析、暂态稳定计算、小干扰静态稳定计算、短路计算、静态和动态等分析计算的基础。电力系统中求解潮流的方法有高斯-赛德尔法、牛顿-拉夫逊法以及派生于牛顿-拉夫逊法的pq分解法(pq法)。pq法收敛速度快、占用内存少，可用于电力系统离线或在线实时潮流计算，是潮流计算的重要方法。因此提高pq法潮流计算速度使其更加适用于实时计算是人们一直追求的目标。

pq法潮流计算中要应用计算节点电流ipi和iqi的节点导纳矩阵y、计算节点电压相角增量δδi和节点电压幅值增量δvi的系数矩阵b′、b″，而传统pq法中对y、b′、b″阵数据的读取及应用等存在以下问题：

(1)y、b′、b″阵数据的存贮方式不理想，存贮单元多、数据文件读写时间长。

1)y、b′、b″阵均为极度稀疏对称矩阵。不考虑元素稀疏性时一般采用简单的y(n，2n)、b′(n-1，n-1)、b″(m，m)数组形式，其中n为系统节点数，m为pq节点数，其存贮空间浪费极大，读写数据文件及后续计算所需时间过长。

2)考虑元素稀疏性的坐标存贮、顺序存贮、链表存贮等方式虽可节省大量存贮单元，但结构复杂，且对角元素与非对角元素分开存贮不能清晰地反映元素之间的对应关系，使得数据读写过程繁琐，不利于数据的快速计算及处理，且其存贮单元数也未达到最佳。

(2)大量零元素的y(n，2n)数组计算ipi、iqi，计算效率极其低下。

(3)对b′(n-1，n-1)、b″(m，m)数组的所有前代和回代方式和方法非最佳。

1)pq法中的p-δ和q-v方程均为常系数线性方程，故传统方法可用lr、ldu、cu三角分解法或因子表法进行求解。但三角分解法需形成和求解2～3个因子阵，还需求解1～2个中间变量矩阵，而因子表法可直接在系数矩阵中建立因子表，计算过程比任何三角分解法更简单易解、计算速度更快。

2)传统pq法中对b′、b″阵的计算用大量零元素的b′(n-1，n-1)、b″(m，m)数组，导致大量的无效计算或大量的非零判断，计算效率低下。

3)传统pq法中对b′、b″阵按行形成因子表及形成因子表后对常数项列矩阵按行前代计算方式不佳，不利于稀疏矩阵技术和对称计算方式的应用，导致计算效率低下。

4)传统pq法未利用y、b′、b″阵元素结构的特点进行计算。如传统因子表法的形成过程中元素的计算需应用消元计算公式，因而计算繁琐复杂，极不利于计算过程的理解和编程；如形成因子表后才对对角元素取倒，未能减少规格化过程中的除法计算，使计算速度无法达到最佳；因子表的形成过程中未能利用对称矩阵结构的特点，无法省略50％非对角元素的计算，大大影响计算速度的提高。

5)传统因子表法中稀疏矩阵技术的应用不到位。因子表的形成过程中稀疏矩阵技术的应用不到位，如未提出非零元素的快速判断方法、计算元素的快速确定方法、元素的对称计算方法、高效的非零元素记录方法等等，其因子表形成过程效率极低；形成因子表后稀疏矩阵技术的应用不到位，如对常数项矩阵的前代过程采用按行方式，无法利用所记录的上三角的非零元素的位置，导致计算效率低下；形成因子表后的回代过程中虽然利用了稀疏矩阵技术，但由于将对角元素和非对角元素分开记录和存放、且未记录各行非零元素的个数，因此计算效率不高。

综上所述，传统因子表法用于pq法潮流计算中，无论数据的存贮方式还是对y、b′、b″阵的计算方式均远未达到最优。

技术实现要素：

为了克服上述现有技术的不足，本发明提出一种电力系统pq法潮流中随机非零元素因子表的形成及应用。本发明方法中对所需应用的y、b′、b″阵元素均按随机顺序仅存储其上三角非零元素，分别构成y(n，d′1)、b′(n-1，d′2)、b″(m，d′3)三个数据文件，可大大减少数据文件读写时间；在pq法潮流计算中，从y(n，d′1)文件写入数据的y(n，d1)数组可大大减少ipi、iqi的计算时间；从b′(n-1，d′2)、b″(m，d′3)文件写入数据的b′(n-1，d2)、b″(m，d3)数组可无需进行非零判断、直接以按列消元方式形成随机顺序的因子表，并将其用于电力系统pq法潮流计算；形成随机顺序因子表过程中，采用按列消元、四角规则、对角元素提前取倒、非零元素记录新方法等技巧；形成随机顺序因子表后，采用按列前代、按行回代，可大大加快pq法潮流计算时间。

本发明是通过以下技术方案实现的，基本步骤如下：

步骤1：定义数组y(n，d1)、b′(n-1，d2)、b″(m，d3)；

步骤2：将对y、b′、b″阵所建立按随机顺序的、仅含上三角非零元素的数据文件y(n，d′1)、b′(n-1，d′2)、b″(m，d′3)数据分别导入y(n，d1)、b′(n-1，d2)、b″(m，d3)数组；

(1)运行pq法潮流程序前，分别对y、b′、b″阵建立随机顺序的上三角非零元素数据文件y(n，d′1)、b′(n-1，d′2)、b″(m，d′3)。三个数据文件基本结构相同，分为非零计数组、对角元素组和非对角元素组。非零计数组存放各行上三角所对应的、不包括对角元素的各行非零元素数s′1i、s′2i、s′3i，分别与其对应的、最大非零元素数为s′1max、s′2max、s′3max；对角元素组分别存放对角元素的行号i和参数；非对角元素组再按小组分别随机存放与该对角元素连接的、上三角非对角元素的列号j和参数。

y(n，d′1)文件均为3列一小组，其中d′1＝3s′1max+4，y(n，d′1)的最大存储单元为n×d′1；但由于以一维数组方式存储，每行的实际列数为3s′1i+4，因此y(n，d′1)的实际存储单元为n×∑(3s′1i+4)。对b′(n-1，d′2)、b″(m，d′3)文件，均2列一小组，其中d′2＝2s′2max+3或d′3＝2s′3max+3，其每行的实际列数为2s′2i+3或2s′3i+3，也有最大和实际存储单元之分。数据文件y(n，d′1)、b′(n-1，d′2)的静态结构分别如表1、表2所示。

表1y(n，d′1)数据文件的静态结构

表2b′(n-1，d′2)数据文件的静态结构

注：表1和表2中所有参数如gii、bii、gi，j1、bi，j1均是初始参数，但并不相同，如表1和表2中的bii完全不同。

b″(m，d′3)数据文件的静态结构与b′(n-1，d′2)相似，只是对表2中的参数如bii、gi，j1、bi，j1等以及变量做如下替换：s′2i→s′3i、s′2max→s′3max、s′2，n-2→s′3，m-1、s′2，n-1→s′3m。

(2)由于数据文件y(n，d′1)、b′(n-1，d′2)、b″(m，d′3)中的列号和参数均按随机顺序的支路数据形成，因此三个文件中元素的列号无需满足.j1＜j2＜…jn-1＜jn条件，但要求三个文件中仅存贮行号i小于或等于列号j的上三角的参数gij、bij。

(3)根据s′1i，将数据文件y(n，d′1)中存储的y阵数据快速导入y(n，d)数组，y(n，d)与y(n，d′1)结构完全相同，且y(n，d)数组中s1i＝s′1i；根据s′2i、s′3i，将数据文件b′(n-1，d′2)、b″(m，d′3)中存储的b′、b″阵数据分别快速导入b′(n-1，d2)及b″(m，d3)数组，b′(n-1，d2)及b″(m，d3)数组的动态结构与b′(n-1，d′2)、b″(m，d′3)文件的静态结构不同，主要差别如下：

1)b′(n-1，d′2)、b″(m，d′3)文件的作用仅仅是存储表2所示的b′、b″阵元素的静态参数，不能直接用于消元计算，其非零元素数s′2i、s′3i不变化。b′(n-1，d2)、b″(m，d3)数组的作用是对被读入的b′(n-1，d′2)、b″(m，d′3)数据进行消元计算，将不断产生新的非零元素，其非零元素数s2i、s3i将不断变化，直至消元完成。此时有s2i＞＞s′2i、s3i＞＞s′3i，因此d2＞＞d′2、d3＞＞d′3。

2)在b′(n-1，d2)、b″(m，d3)数组中，将b′(n-1，d′2)、b″(m，d′3)文件非对角元素组的一小组2列扩展为3列，增加1列对参数b′ij规格化后的参数b″ij，并在非对角元组的右侧继续增加部分存储单元以存放消元过程中随机产生的新的非零元素。

3)将b′(n-1，d′2)、b″(m，d′3)文件的数据全部对应导入到b′(n-1，d2)、b″(m，d3)数组，包括s′2i、s′3i，但非对角元素的数据均导入给b′(n-1，d2)、b″(m，d3)数组对应的第1～2列。

4)消元前b′(n-1，d2)、b″(m，d3)数组中的s2i、s3i初始值与b′(n-1，d′2)、b″(m，d′3)文件中的非零元素数s′2i、s′3i相同，但随着消元过程的进行s2i、s3i的值将不断变化。

b′(n-1，d2)数组的动态结构如表3。

表3b′(n-1，d2)数组的动态结构

注：表3中b′ii、b′i，j1、b′i，j2参数是对表1和表2中的bii、bi，j1、bi，j2初始参数计算后的参数，b″i，j1、b″i，j2等是对参数b′i，j1、b′i，j2规格化后的参数。

b″(m，d3)数据文件的动态结构与b′(n-1，d2)相似，只是对表3中的参数b′ii、b′i，j1、b′i，j2和b″i，j1、b″i，j2等以及变量做如下替换：s2i→s3i、s2，n-2→s3，m-1、s2，n-1→s3m。

步骤3：对b′(n-1，d2)、b″(m，d3)数组进行基于对称稀疏矩阵技术的随机对称消元形成因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′；

(1)传统方法中b′(n-1，n-1)、b″(m，m)数组形成因子表b′(n-1，n-1)(^n-2)′、b″(m，m)^(m-1)′

传统方法中对b′(n-1，n-1)、b″(m，m)数组消元形成因子表的计算过程完全依靠消元计算公式，对于计算原理的理解和应用、特别是对于编程极为不便；且传统方法以按行消元方式形成因子表，使得对称稀疏矩阵技术和对称算法的应用难以实现。但此处为着重说明和比较传统方法中对规则且顺序数组的消元和本发明方法中对不规则且随机顺序数组的消元，对传统方法也采用按列消元方式，并用四角规则进行消元计算。

1)四角规则在b′(n-1，n-1)、b″(m，m)数组中的应用。

对第k列元素消元前后的b′(n-1，n-1)^(k-1)′、b″(m，m)^(k-1)′数组的简化形式如式(1)。

各元素在简化矩阵中的位置及定义如下：

对角元素(终值，参考元素)；

交叉元素规格化前′(后″，终值)，对角元素同行以右；

消元元素(终值)，对角元素同列以下；

计算元素前值和新值(除将赋值给第k+1列的元素外，均为中间过渡值)，位于与非零的消元元素同行、非零的交叉元素同列的交叉点上。

对元素消元，按传统方法的消元计算公式可得计算式如下：

但直接根据式(1)中各相关元素在矩阵中的位置，也可直接写出各计算元素的表达式，即以对角元素为参考元素：“计算元素新值＝计算元素前值-消元元素×规格化后的交叉元素”，即只需计算对角元素以下的消元元素所在行和对角元素以右的交叉元素所在列交叉点上的元素。由于这四个元素均在矩形的四个角上因此根据消元过程中各相关元素的位置，可无需消元计算公式直接用四角规则写出上述计算式。

2)b′(n-1，n-1)、b″(m，m)数组中非零元素的快速判断和计算元素的快速确定。

对称矩阵以按列消元方式进行消元计算时，其对角元素以右非零的交叉元素和对角元素以下非零的消元元素的位置始终对称。因此式(1)中，若对角元素以右则可得对角元素以下而根据对角元素以右非零的交叉元素所在列和对角元素以下非零的消元元素所在行的交叉点就可确定有效的计算元素为四个。

3)对b′(n-1，n-1)、b″(m，m)数组中元素进行对称计算。

对于对称矩阵，消元时用对称算法可省去下三角元素的计算。如式(1)中对角元素以右规格化前的元素与对角元素以下的元素完全对称，而规格化后的元素与是不完全对称。利用该特性，在对第k列的元素按列消元的过程中，仅需计算各消元元素所在行对角元素及以右的元素，即仅计算式(1)中的三个元素，而不用计算其所在行对角元素以左的元素而在对第j-1列元素消元完成后和第j行元素规格化前，先将第j行的非零元素赋给第j列元素，然后对第j行的元素规格化得元素，再继续对第j列的元素消元。这种计算方式可使所有对角元素以下元素均直接通过赋值获得、而无需计算，从而大大简化计算。

4)b′(n-1，n-1)、b″(m，m)数组中非零元素的记录。

程序中记录第一次对b′(n-1，n-1)、b″(m，m)数组消元过程中每行上三角非零元素的个数s2i、s3i和更新的非零元素的参数以及新产生的非零元素的列号及参数，以便在后续的前代和回代过程重复利用，可大大提高计算效率。

(2)本方法对b′(n-1，d2)、b″(m，d3)数组形成因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′；

1)用四角规则对b′(n-1，d2)、b″(m，d3)数组元素进行消元计算；

由于b′(n-1，d2)、b″(m，d3)数组的结构不对称，且其元素随机存放，因此对b′(n-1，d2)、b″(m，d3)数组的消元也是随机进行。由于b′(n-1，d2)、b″(m，d3)数组中非对角元素组是以小组为单位存放，每小组第1列为列号；第2列为规格化前的上三角元素如b′i，j1，与下三角消元元素完全相等；第3列为对第2列元素b′i，j1规格化后的上三角元素如b″i，j1，也就是交叉元素。因此对b′(n-1，d2)、b″(m，d3)数组中非零元素消元，就是对非对角元素组中各小组的第2列元素消元。同样以第i行对角元素为参考元素，将非对角元素组中各小组所有的第3列规格化后的元素b″ij作为交叉元素，将各小组所有第2列规格化前元素b′ij的列号j和行号i互换，即可得到第i列对角元素以下第j行的消元元素b′ji。对b′ji元素消元，只需将b′ji元素分别与第i行的所有元素进行比较，找到第j行与第i行所有交叉元素的交叉点进行计算即可，此时仍可直接按“计算元素新值＝计算元素前值-消元元素×规格化后的交叉元素”的四角规则对数组b′(n-1，d2)、b″(m，d3)元素进行消元以快速形成因子表，只是此时相应的元素并不在规则矩形的四个角上。

2)b′(n-1，d2)、b″(m，d3)数组中非零元素的快速判断和计算元素的快速确定；

a.由于b′(n-1，d2)、b″(m，d3)数组中仅有非零元素，因此均无需进行非零判断。

b.将b′(n-1，d2)、b″(m，d3)数组中各小组所有第2列规格化前元素b′ij、b′ik的列号j、k均与行号i互换，即可得到第i列对角元素以下第j行和第k行的消元元素b′ji、b′ki。此时第i列各行的b′ji、b′ki元素与第i行规格化后第3列的各元素b″ij、b″ik在交叉点上、且位于上三角的元素，即为需要计算的计算元素。如在第j行的第k列的位置上已有元素b′jk，只需将计算得到的b′jk的新值替换其原值；若在第j行的第k列的位置上无元素，则将新产生的非零元素b′jk的列号及其参数存放到第j行非对角组紧靠右侧新增加小组的第1～2列中，并且将该行的s2j加1或s3j加1，即可直接完成对计算元素的计算。

3)b′(n-1，d2)、b″(m，d3)数组中元素的对称计算；

根据b′和b″阵的对称性可知，b′(n-1，n-1)或b″(m，m)数组中对角元素以右非零的非对角元素规格化前与对角元素以下非零的非对角元素完全相同，因此在消元过程中，可不用计算各行对角元素以左的下三角元素，而是在对第i行元素规格化之前通过赋值得到对角元素以下的第i列元素，再对第i行元素规格化，然后再对第i列元素消元计算。

由于在b′(n-1，d2)、b″(m，d3)数组中每个非对角元素小组分为3列，因此消元计算中可分别将第k行对角元素以右各规格化前的第2列元素如b′ki的列号i与行号k互换，互换后成为对角元素以下的消元元素b′ik，再将此时消元元素b′ik的行号i分别与第k行所有规格化后的第3列元素b″kj的列号j进行比较，并按下述三种情况处理：

a.如果互换后所得的消元元素的行号i大于第k行规格化后元素的列号j，则该元素位于下三角，无需计算；

b.如果互换后所得的消元元素的行号i等于第k行规格化后元素的列号i，则该元素为对角元素，可将计算后的新值直接替换第i行原对角元素的前值；

c.如果互换后所得的消元元素的行号i小于第k行规格化后元素的列号j，则该元素为上三角元素，则必须计算该元素。将该计算元素的列号j分别与第i行非零元素的列号进行比较，如果第i行有相同的列号j，则将计算后元素的新值直接替换第i行、第j列中原该小组元素第2列的前值；若果没有相同的列号j，则将其列号j及计算后的值直接存放在第i行非对角元素组最右侧紧邻的新小组的第1～2列。

传统方法的b′(n-1，n-1)或b″(m，m)数组中如果不计算下三角元素，一般在对第i行元素规格化之前需先将其赋值给第i列的下三角元素。而本发明方法的b′(n-1，d2)、b″(m，d3)数组中只是将规格化前的参数和规格化后的参数分开存放，无需赋值。

4)数组b′(n-1，d2)、b″(m，d3)中计算元素的存放方式

传统方法b′(n-1，n-1)、b″(m，m)数组中，所计算的非零元素交叉点上的元素均存放在对应的交叉点上。而本发明方法b′(n-1，d2)、b″(m，d3)数组中，所计算的非零元素交叉点上的元素，无论非零元素的新值还是新产生的非零元素均存放在相应小组的第2列，在对该行元素规格化后，其第3列才会出现相应的元素。

完成上述计算可得本发明方法随机顺序排列的因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′。

步骤4：根据y(n，d1)数组计算ipi、iqi；

(1)将传统法中ipi、iqi的计算式改写如式(2)、(3)：

将式(2)、(3)中对ipi、iqi的计算分解成的对n个节点电流增量δip，i1～δip，in、δiq，i1～δiq，in计算的叠加。由于y(n，d1)数组仅存贮y阵上三角的非零元素，因此不能用y(n，d1)数组根据式(2)、(3)直接计算ipi、iqi。但由于y阵对称，可将ipi、iqi计算分成左右两部分，即ipi＝ip.i-left+ip.i-right和iqi＝iq.i-left+iq.i-right。右部分的ip.i-right、iq.i-right可根据y阵第i行对角元素及以右的上三角元素，即根据y(n，d1)数组直接完成的计算；左部分的ip.i-left、iq.i-left需根据y阵第i行对角元素以左的下三角元素计算获得，而这部分只能在第i行前面各行，如第j行(j＜i)中求取右部分的ip.j-right、iq.j-right时通过对称性计算获得ip.i-left、iq.i-left的部分计算结果。

此外，传统法计算ipi、iqi的式(2)、(3)中一般用到y阵第i行的所有元素，但实际有效的只有该行的非零元素。假设式(2)、(3)中除对角元素i外，仅有j、k、m三列元素非零，且j＜i和i＜k＜m，因此式(2)、(3)可简化成式(4)、(5)。

根据式(4)计算第i行的ipi时，其左部分电流ip.i-left＝δip.ij，即在计算第j行的右部分电流δip.ji时，可根据对称性同时计算第i行的δip.ij。因此在计算第i行的ipi时，其左部分的所有电流实际上已经通过前面各行中计算右部分电流时的根据对称性得到，所以计算第i行的ipi时，只需将前面计算的左部分电流ip.i-left的各个增量累加，而根据y(n，d1)数组直接计算右部分电流ip.i-right，然后两者叠加则可得到ipi。但在根据y(n，d1)数组计算第i行右部分电流ip.i-right的δip.ik、δip.im时，同时要根据对称性计算第k、m行的左部分电流δip.ki、δip.mi，以便在计算第k、m行的电流时直接进行累加。

iqi计算过程同上。

步骤5：根据因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′中对角元素组和非对角元素组各小组的第2列参数分别对δp/v、δqv阵前代计算得(δp/v)^(n-2)′、(δq/v)^(m-1)′阵；

将因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′中对角元素组和非对角组各小组第2列规格化前的参数及作为下三角数据，对δp/v、δq/v阵进行前代计算得到(δp/v)^(n-2)′、(δq/v)^(m-1)′。由于因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′中只含非零元素，因而在形成因子表后对δp/v、δq/v阵的前代计算中也无需非零判断，可大大提高计算效率。

用b′(n-1，d2)^(n-2)′因子表对δp/v阵前代计算得(δp/v)^(n-2)′，其元素计算式如式(6)。

用b″(m，d3)^(m-1)′因子表对δq/v阵前代计算得(δq/v)^(m-1)′，其元素计算式如式(7)。

其中，为第i行存放的非对角组中、从j1、j2、---开始计数、到第k个非对角元素中规格化前的参数，均在各小组的第2列。

步骤6：根据因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′中非对角元素组各小组的第3列参数分别和(δp/v)^(n-2)′、(δq/v)^(m-1)′阵回代计算求取δδi、δvi；

由于因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′中非对角组各小组第3列参数是规格化后的上三角数据，因此可将其和(δp/v)^(n-2)′、(δq/v)^(m-1)′阵进行回代计算以求取δδi、δvi。同样由于因子表中只有非零元素，因而也可大大提高回代计算效率。

δδi、δvi的计算式如(8)、(9)。

其中，为第i行存放的非对角组中、从j1、j2、---开始计数、到第k个非对角元素中规格化后的参数，均在各小组的第3列。

步骤7：判断是否满足收敛条件|δpi、δqi|max≤ε＝10^-5，如果不满足，则利用本次迭代得到的δi、vi继续跳转到步骤4重新计算；如果满足，则执行步骤8；

步骤8：计算平衡节点的功率及支路功率并输出计算结果。

本发明方法与传统的pq分解法相比，具有以下优点：

(1)对y、b′、b″阵元素建立的y(n，d′1)、b′(n-1，d′2)、b″(m，d′3)数据文件以随机顺序仅存储上三角非零元素，可大大加快数据文件的读写速度。

(2)将随机顺序静态结构的y(n，d′1)、b′(n-1，d′2)、b″(m，d′3)文件数据分别导入y(n，d1)、b′(n-1，d2)、b″(m，d3)数组，其中y(n，d1)数组与y(n，d′1)文件结构一样，用于快速计算ipi、iqi；而动态结构b′(n-1，d2)、b″(m，d3)数组与b′(n-1，d′2)、b″(m，d′3)文件结构完全不同，可大大加快上述数组的前代和回代的计算速度。

(3)基于对称稀疏矩阵技术对随机存放的非零元素进行随机对称消元快速形成相应的因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′，可大大加快因子表的形成速度。

(4)利用因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′中对角元素组及非对角组各小组第2列参数作为下三角数据，分别对δp/v、δq/v阵前代计算得(δp/v)^(n-2)′、(δq/v)^(m-1)′阵，可大大加快对δp/v、δq/v阵的前代计算速度。

(5)利用因子表b′(n-1，d2)^(n-2)′、b″(m，d3)^(m-1)′中非对角组各小组的第3列参数作为上三角数据，可大大加快求取δδi、δvi的回代计算速度。

附图说明

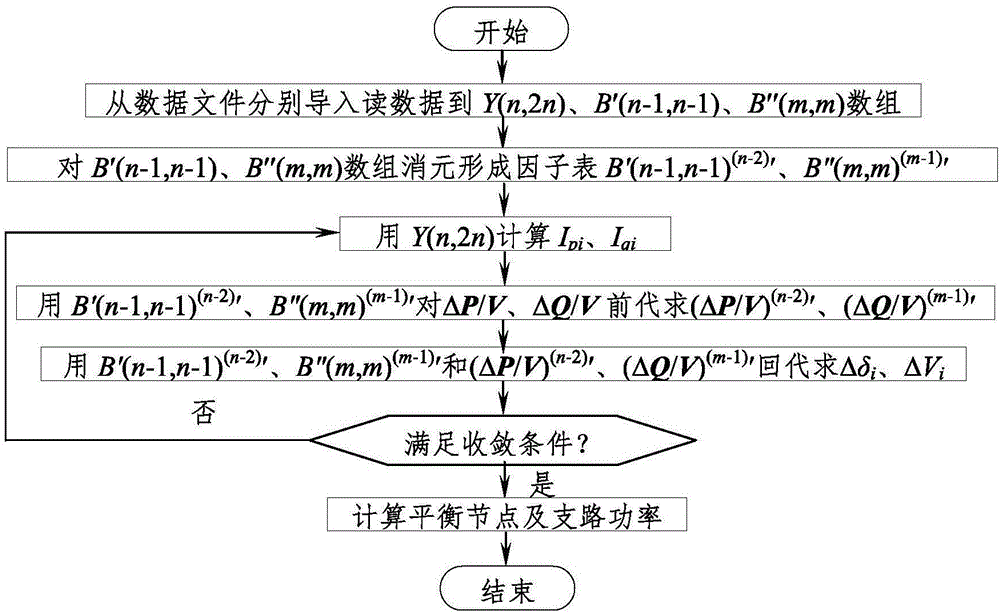
图1为传统方法求取极坐标pq分解法潮流的计算流程图。

图2为本发明方法求取极坐标pq分解法潮流的计算流程图。

具体实施方式

本发明将通过以下实施例作进一步说明。

实施例1：分别用传统方法和本发明方法对ieee-14～-118节点系统进行极坐标pq分解法潮流计算，分别比较其读写数据文件、形成因子表和潮流计算时间。比较结果如表4所示。

表4本发明方法与传统方法求解ieee各系统pq分解法潮流所需时间比较

tc.w、tc.r：传统方法写读y(n，2n)、b′(n-1，n-1)、b″(m，m)数据文件时间；

tn.w、tn.r：本发明方法写读y(n，d′1)、b′(n-1，d′2)、b″(m，d′3)数据文件时间；

tn.w/tc.w、tn.r/tc.r：本发明方法写读数据文件时间与传统方法时间的百分比；

tc.ff、tc.pf：传统方法对y(n，2n)、b′(n-1，n-1)、b″(m，m)数组形成因子表或潮流计算时间(不含读数据文件)；

tn.ff、tn.pf：本发明方法对y(n，d1)、b′(n-1，d2)、b″(m，d3)数组形成因子表或潮流计算时间(不含读数据文件)；

tn.ff/tc.ff、tn.pf/tc.pf：本发明方法形成因子表或潮流计算与传统方法时间的百分比。

以ieee-118节点系统为例，本发明方法与传统方法的计算结果比较分析如下：

写数据文件时间仅为传统方法的9.11％；读数据文件时间仅为15.29％；形成因子表时间仅为3.61％；潮流计算时间(不含读数据文件)仅为21.10％。因此，本发明方法与传统方法相比，写读数据文件、形成因子表、潮流计算等计算速度均大大提高，且其优势随着电力系统规模的增大而增加。

本方法可以采用任何一种编程语言和编程环境实现，这里采用c++语言，开发环境是visualstudio2013，运行平台是intel(r)corei7-4790cpu@3.60ghz，内存8.00gb。