有限长微声学器件的积木式快速有限元仿真方法及系统与流程

本发明涉及微声学领域，具体地，涉及有限长微声学器件的积木式快速有限元仿真方法及系统。

背景技术：

微声学器件日益精细化设计与理论研究发展均迫切需要更加精确和通用的方法实现复杂器件模拟。以声表面波(saw)器件为例，对器件中有限长栅格阵或周期性被破坏的非同步栅格区域的仿真，传统的耦合模(com)模型等具有周期性边界条件假设的模拟工具已经无法满足要求。格林函数结合有限元方法一度是国际公认的最严格的有限长saw器件精确仿真模型，但随着温度补偿、新型压电薄膜以及任意形状甚至复合材料电极等新型saw器件的涌现，采用有限元(fem)代替fem/bem逐渐成为研究的热点。然而，一个完整的有限长saw器件的fem模型通常具有数千万计的自由度，需要耗费庞大的计算资源与计算时间。对于其它微声学器件的fem仿真，为了满足仿真精度的要求，通常在每个波长内划分足够多的网格，因此密集的网格划分而导致的庞大计算成本同样使得精确仿真成为实际工程设计中的禁区。

经对现有仿真技术方面文献检索发现，文献“hierarchicalcascadingin2dfemsimulationoffinitesawdeviceswithperiodicblockstructure(koskelaetal.,ieeeultrasonicssymposium(ius),2016)”在二维层面上报道了基于hierarchicalcascading(hct)技术的快速fem仿真方法，该方法充分利用了saw器件中周期性结构特点，对整个器件进行周期性划分，划分后的子模块包含一根指条甚至为不包含任何指条。因为描述相同子模块的有限元方程是相同的，故通过对每一单独子模块进行仿真求解，再通过级联各单独子模块响应的方式可得到整个器件的响应，实现了对saw器件的快速精确仿真，该方法仅需要子模块边缘处的自由度并存储，因此计算资源的消耗独立于器件的长度。而文献，“full3dsimulationofsawresonatorsusinghierarchicalcascadingfem”(solaletal.,ieeeultrasonicssymposium(ius),2017)将该方法拓展为全三维情况，并进行了仿真精度的论证，从而进一步验证了该方法的有效性。

基于hct技术，有限长周期结构saw器件的完全有限元仿真所需的庞大计算资源可大幅度降低，但由于该技术本身基于saw器件周期性结构特点，随着日益复杂的微声学器件需要一体化、精细化设计，例如saw辨识标签，器件本身不具备众多周期性重复单元，而使得利用hct技术的fem仿真，不得不计算多块基本单元进行拼接组装，从而大大降低该方法的性能；而随着移动网络从4g到5g的飞跃，3.5ghz以上的工作频段将需要更加精细化、复杂化、小型化的微声学器件，因此对于微声学器件的功率耐受性研究也变得十分重要，而采用hct-fem计算微声学器件表面功率流，需要反演运算出已经消去的内部自由度，而增加大量工作时间，从而使得基于器件周期性的hct技术变得更加难以利用。

经对上述文献的调研与实验论证，我们发现虽然采用hct技术的fem方法可以使具备周期性的部分saw器件的精确仿真成为可能，但是由于众多微声学器件不具备周期性特点，因此迫切需要一种“通用性”的有限长微声学器件精确仿真方法。因此，如何实现满足复杂结构、精细化设计的微声学器件的快速精确仿真，成为了目前国际微声学仿真技术领域亟待解决的关键问题。

技术实现要素：

针对现有技术中的缺陷，本发明的目的是提供一种有限长微声学器件的积木式快速有限元仿真方法及系统。

根据本发明提供的一种有限长微声学器件的积木式快速有限元仿真方法，包括：

模型获取步骤：获取微声学器件物理模型；

分组步骤：对微声学器件物理模型进行特征识别和分组，将相同特征的部分分在一组；对每组内的特征子单元进行分割；

有限元计算步骤：选取每个组成部分中的任意一个特征子单元建立有限元模型进行有限元计算，得到所选取的特征子单元的有限元计算结果；

拼接步骤：将所选取的特征子单元的有限元计算结果代替对应组内其他特征子单元的有限元计算结果，对组内的特征子单元进行拼接，得到各个组的有限元计算结果；将各个组的有限元计算结果进行拼接，得到微声学器件物理模型的有限元计算结果。

较佳的，还包括：

功能特性计算步骤：对微声学器件物理模型的有限元计算结果进行功能特性计算，得到所需的结果。

较佳的，在拼接步骤对各个组的有限元计算结果进行拼接时，保留各个组的边缘自由度。

较佳的，在拼接步骤得到的微声学器件物理模型的有限元计算结果中加入渐变的衰减区域，所述衰减区域位于微声学器件物理模型的四周。

根据本发明提供的一种有限长微声学器件的积木式快速有限元仿真系统，包括：

模型获取模块：获取微声学器件物理模型；

分组模块：对微声学器件物理模型进行特征识别和分组，将相同特征的部分分在一组；对每组内的特征子单元进行分割；

有限元计算模块：选取每个组成部分中的任意一个特征子单元建立有限元模型进行有限元计算，得到所选取的特征子单元的有限元计算结果；

拼接模块：将所选取的特征子单元的有限元计算结果代替对应组内其他特征子单元的有限元计算结果，对组内的特征子单元进行拼接，得到各个组的有限元计算结果；将各个组的有限元计算结果进行拼接，得到微声学器件物理模型的有限元计算结果。

较佳的，还包括：

功能特性计算模块：对微声学器件物理模型的有限元计算结果进行功能特性计算，得到所需的结果。

较佳的，在拼接模块对各个组的有限元计算结果进行拼接时，保留各个组的边缘自由度。

较佳的，在拼接模块得到的微声学器件物理模型的有限元计算结果中加入渐变的衰减区域，所述衰减区域位于微声学器件物理模型的四周。

与现有技术相比，本发明具有如下的有益效果：

(1)本发明利用“积木原理”，更具“通用性”：对微声学器件各个部分进行分割，并对每一个特征子单元进行仿真、拼接、组装，从而得到完整的微声学器件有限元计算结果，有别于hct技术，该方法不受周期性结构限制而更具有通用性，使得利用有限元方法快速计算复杂微声学器件成为可能；

(2)本发明利用“积木原理”，更具“简易性”：使原本具备复杂结构的微声学器件可以分割为若干个简单的特征子单元分别进行计算，降低了原本需要大量专业知识积累的微声学器件仿真门槛，十分易于操作；

(3)本发明利用“积木原理”，更具“快速性”：复杂结构的微声学器件由若干特征子单元拼接构成，软件只需对特征子单元进行有限元仿真，便可以通过拼接算法得到完整器件的有限元计算结果，从而对传统有限元仿真进行加速。

(4)本发明利用“积木原理”，更具“功能性”：在进行电极部分与基底部分拼接过程中，由于基底表面自由度全部保留，在施加电连接边界条件后易于计算出表面功率流分布情况，而无需反演计算的大量工作时间。

本发明仅需对器件的局部进行有限元计算即可通过拼接的方式获得完整器件的有限元计算结果，因此可以对传统的有限元方法在不降低精确度的情况下进行加速。本发明一方面可以平衡微声学器件仿真的实效性与精确性之间的矛盾，另一方面积木式拼接方法使得在处理复杂微声学器件结构的精确仿真中可以发挥重要作用。

附图说明

通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：

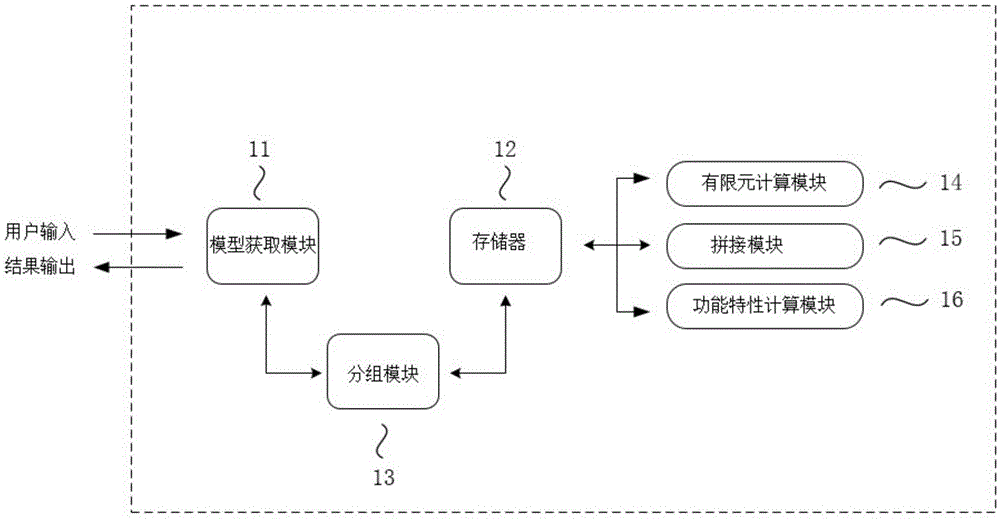
图1为本发明的总体架构图；

图2为本发明的逻辑图；

图3为本发明实施例中压电基底部分的拼接结果示意图；

图4为本发明实施例中器件四周衰减区域施加示意图；

图5为本发明实施例中需要计算的不同形状的电极；

图6为本发明实施例中对于各组仿真结果拼接后的结果示意图。

具体实施方式

下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变化和改进。这些都属于本发明的保护范围。

如图1和图2所示，本发明提供的一种有限长微声学器件的积木式快速有限元仿真方法，包括：

模型获取步骤：获取微声学器件物理模型；

分组步骤：对微声学器件物理模型进行特征识别和分组，将相同特征的部分分在一组；对每组内的特征子单元进行分割；

有限元计算步骤：选取每个组成部分中的任意一个特征子单元建立有限元模型进行有限元计算，得到所选取的特征子单元的有限元计算结果；

拼接步骤：将所选取的特征子单元的有限元计算结果代替对应组内其他特征子单元的有限元计算结果，对组内的特征子单元进行拼接，得到各个组的有限元计算结果；将各个组的有限元计算结果进行拼接，得到微声学器件物理模型的有限元计算结果。在对各个组的有限元计算结果进行拼接时，保留各个组的边缘自由度，便于直接得到微声学器件的表面应力、应变及能量分布。在得到的微声学器件物理模型的有限元计算结果中加入渐变的衰减区域，衰减区域位于微声学器件物理模型的四周。加入渐变的衰减区域来替代目前有限元法仿真微声学器件时广泛采用的pml层，但器件底部仍采用pml层。从物理模型上看，该渐变衰减区域位于模型的四周，从而吸收截断边界处的反射声波。

功能特性计算步骤：对微声学器件物理模型的有限元计算结果进行功能特性计算，得到所需的结果。

如图1和图3所示，在上述一种有限长微声学器件的积木式快速有限元仿真方法的基础上，本发明还提供一种有限长微声学器件的积木式快速有限元仿真系统，包括：

模型获取模块11(输入输出接口)：获取微声学器件物理模型；

分组模块13(处理器)：对微声学器件物理模型进行特征识别和分组，将相同特征的部分分在一组；对每组内的特征子单元进行分割；

有限元计算模块14：选取每个组成部分中的任意一个特征子单元建立有限元模型进行有限元计算，得到所选取的特征子单元的有限元计算结果；

拼接模块15：将所选取的特征子单元的有限元计算结果代替对应组内其他特征子单元的有限元计算结果，对组内的特征子单元进行拼接，得到各个组的有限元计算结果；将各个组的有限元计算结果进行拼接，得到微声学器件物理模型的有限元计算结果。在对各个组的有限元计算结果进行拼接时，保留各个组的边缘自由度，便于直接得到微声学器件的表面应力、应变及能量分布。在得到的微声学器件物理模型的有限元计算结果中加入渐变的衰减区域，衰减区域位于微声学器件物理模型的四周。加入渐变的衰减区域来替代目前有限元法仿真微声学器件时广泛采用的pml层，但器件底部仍采用pml层。从物理模型上看，该渐变衰减区域位于模型的四周，从而吸收截断边界处的反射声波。

功能特性计算模块16：对微声学器件物理模型的有限元计算结果进行功能特性计算，得到所需的结果。

存储器12中不仅需要对有限元计算模块14的结果进行存储，也支持拼接模块15和功能特性计算模块16的消耗巨大的矩阵运算。

如图3至图6所示，以下通过以具体实施例进行说明：

以声表面波谐振器为例，可以将其划分为压电基底和电极两个组成部分。

将压电基底部分二次分割得到一条从上至下分别为压电基底与底部完美匹配层的压电基底局部模型；对电极部分进行特征识别，将特征不同的电极视为电极部分的局部模型。

通过对电极部分与压电基底部分的有限元计算结果执行拼接算法，可以得到完整声表面波谐振器的有限元计算结果。

通过对压电基底局部模型的拼接可以得到压电基底部分的完整有限元计算结果，通过对电极部分的局部模型进行拼接可以得到电极部分的完整有限元计算结果。

将其局部模型作为特征子单元进行一次拼接可以得到以2个局部模型为特征子单元的有限元计算结果，将2个局部模型构成的特征子单元，再进行一次拼接，可以得到4个局部模型构成的特征子单元，以4个局部模型构成的特征子单元再次拼接，得到8个局部模型构成的特征子单元，直到完成整个压电基底部分的有限元计算，该方法只需对局部模型进行一次有限元计算，通过拼接算法可以得到整个器件的有限元计算结果，从而对传统有限元方法进行加速。

压电基底可以为层状键合基底，电极可以为任意形状的层状复合电极。

首先，用户可以根据自己的需求采用图形化或输入参数编程的形式在输入输出接口11定义自己的微声学器件物理模型，而后软件将对用户定义的物理模型进行特征识别，并将特征不同的部分进行第一次切割后完成分组，并再次对组内开始第二次切割完成组内各个特征子单元的分割，至此一个完整的微声学器件被软件划分为几个组成部分，而每个组成部分又包含若干个特征子单元。其次，选取组内的特征子单元(即一个组成部分中的任意一个特征子单元)建立有限元模型并调用软件中的有限元计算模块14完成各个组特征子单元的计算，而后调用软件中的拼接模块15完成各个组内特征子单元的拼接，从而得到各个组的有限元计算结果并存储于存储器12中。再次，调用拼接模块15对存储于内存12中的各个组的有限元计算结果进行拼接并直到拼接完成整个器件，从而得到完整器件的

有限元计算结果。最后，调用功能特性计算模块16完成用户指定的功能，例如输出器件的响应曲线或提取表面功率流分布图。

如图6所示，以层状键合基底，层状复合材料声表面波谐振器为例，其中1～3为采用不同材料键合的基底，7～9为采用不同材料键合的复合材料的电极，4为pml完美匹配层。执行该软件可以将原本如图6的完整声表面波谐振器模型划分为图3压电基底部分，图5各种特征不同的电极部分等几个组成部分，而后软件并进行第二次分割完成组内各个基本单元的划分，其中组内周期性结构采用省略号的形式代替。挑选出组内的一个特征子单元调用有限元计算模块14完成有限元求解并调用拼接模块15进行组内级联如图3所示可以得到各个组成部分的有限元计算结果，例如如图3的级联操作可以得到图4的压电基底部分有限元计算结果。对图4所示的压电基底部分有限元结果中的5和6区域施加衰减(衰减形式从疏到密依次增大)用于吸收电极区域激发的表面声波，防止边缘反射而对仿真精度的影响。最后，将图3与图5的整体计算结果调用拼接模块15进行拼接，从而得到图6所示的整体器件有限元计算结果。最后调用功能特性计算模块16完成用户指定的功能，例如计算导纳曲线。

本发明的工作原理在于，将原本具备复杂形态、在有限元仿真中需要耗费庞大计算资源的微声学器件通过“积木原理”划分为几个组成部分，通过对各个组成部分内特征子单元的有限元计算，即可通过级联算法得到整个微声学器件的有限元计算结果。

有别于hct技术，本发明可以满足日益复杂的微声学器件的精细化设计仿真需求，在器件具备一定复杂程度的基础上，该软件仍然可以利用有限元法快速计算出微声学器件的响应结果与表面功率流分布情况。

本领域技术人员知道，除了以纯计算机可读程序代码方式实现本发明提供的系统及其各个装置、模块、单元以外，完全可以通过将方法步骤进行逻辑编程来使得本发明提供的系统及其各个装置、模块、单元以逻辑门、开关、专用集成电路、可编程逻辑控制器以及嵌入式微控制器等的形式来实现相同功能。所以，本发明提供的系统及其各项装置、模块、单元可以被认为是一种硬件部件，而对其内包括的用于实现各种功能的装置、模块、单元也可以视为硬件部件内的结构；也可以将用于实现各种功能的装置、模块、单元视为既可以是实现方法的软件模块又可以是硬件部件内的结构。

以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变化或修改，这并不影响本发明的实质内容。在不冲突的情况下，本申请的实施例和实施例中的特征可以任意相互组合。