面向加工实时监控的切削仿真实现方法与流程

本发明涉及的是一种机械加工领域的技术，具体是一种面向加工实时监控的切削仿真实现方法。

背景技术：

切削仿真技术是制造工艺的仿真优化技术中的重要内容，相比于常规的切削仿真算法，面向加工实时监控的切削仿真技术提出了更多的要求：首先，实时要求切削算法需要有更快的计算速度，以实现与实际加工过程的同步显示；其次，在实际生产中，制造车间智能化的过程通常并非一步到位，而是在现有制造设备的基础上逐步升级，考虑到工厂现有的切削设备种类繁多，自带控制系统接口的兼容性不一，不便于共享预设的切削工艺参数、例如刀具的预设轨迹等，这就要求切削算法能够缺失预定切削工艺参数的条件下完成仿真计算。

技术实现要素：

本发明针对现有技术存在的上述不足，提出一种面向加工实时监控的切削仿真实现方法，通过优化多面体三向深度元素(depthelement，dexel)化实时建模算法的数据存储和搜索结构、以及刀具的几何仿真模型，提高数控切削(包括车削和铣削)实时仿真过程的仿真速度，实现面向加工实时监控的切削仿真。

本发明是通过以下技术方案实现的：

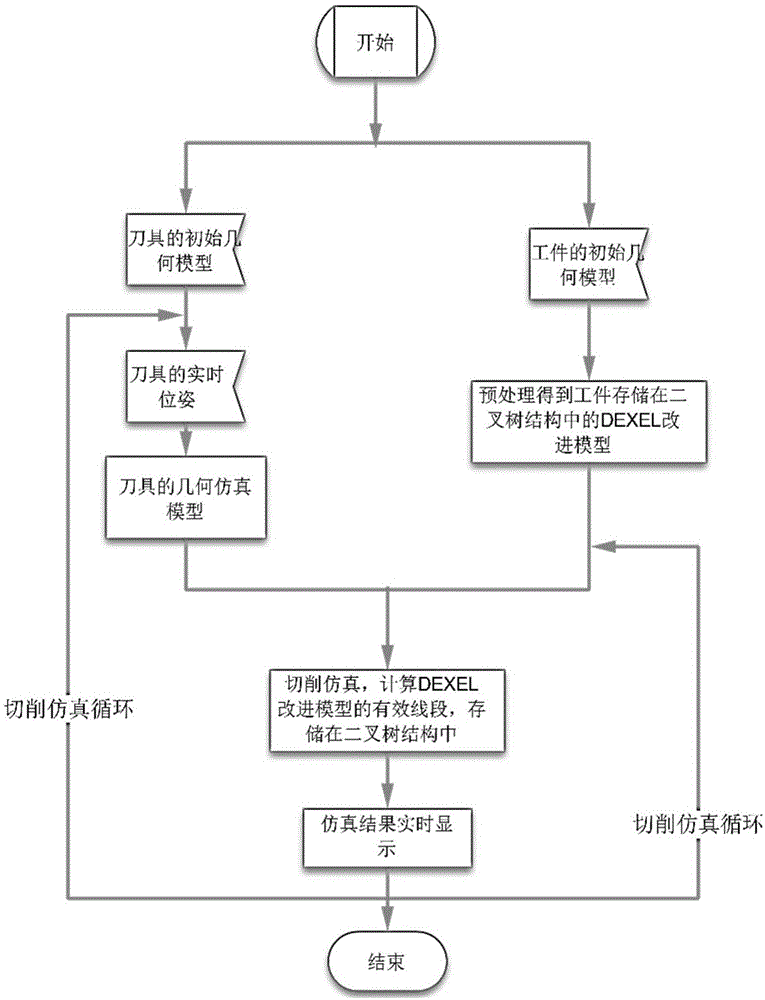
本发明涉及一种面向加工实时监控的切削仿真实现方法，首先对刀具建立刀具的几何仿真模型，同时对工件建立工件的dexel改进模型，然后使用刀具的几何仿真模型和工件的dexel改进模型进行切削仿真运算，并得到更新后的工件的dexel改进模型，最后将其构造为三角面片显示模型，实现实时显示。

所述的刀具的几何仿真模型，指由已知刀具的初始几何模型和刀具位姿的实时传感信息运算得到的近似替代刀具的包络体的刀具实时仿真模型的集合。

所述的工件dexel改进模型，通过dexel改进模型的预处理得到，整个切削仿真过程只需要进行一次dexel改进模型的预处理，具体过程包括：

1)在工件的坐标系内，构造工件的aabb包围盒；

2)构造包围盒内分别沿x、y、z三个轴向直线段组群，这些直线段组群由包围盒截取dexel射线组群而得到；

3)构造二叉树结构存储有效线段：对3d包围盒的xoy面进行二叉空间分割，构造时按照xoy面上的x向和y向进行二分法取直线，该直线段与2d包围盒xoy面上的二叉分割树对应；

4)构造有效线段，取每末层小包围盒的中心点，作为生成射线在xoy面上的坐标，有效线段是由生成射线与工件面片组群求交后得到的线段，它代表工件一段实体。对于一条生成线，可以存在0条或多条有效线段。使用二叉树存储模型存储有效线段。

所述的构造二叉树结构存储有效线段，具体的过程包括：

第1步：确定最终分割尺度，即未来相邻生成线之间的间距值δ；

第2步：对于包围盒的xy-zmin面，校验x向长度和y向长度，对较长的一个进行一次分割，校验分割后获得小包围盒边长，并当两个边长都小于分割尺度值δ时停止分割，最后将多个2d包围盒按照层次组成2d包围盒二叉树模型。

经过改进后的dexel模型，不仅继承了原有模型的全部优点，还由于使用了二叉树结构的存储和搜索方式，显著提高了仿真运算速度，适用于三轴铣削、钻削过程的实时仿真。

所述的切削仿真运算，具体过程包括：

a)在工件坐标系内，构造刀具的aabb包围盒；

b)计算两个包围盒的重叠区域，通过二叉树存储结构进行搜索，确定重叠区域内的三个坐标轴方向的有效线段组群；

c)用刀具的几何仿真模型对重叠区域内的工件的每个有效线段做布尔差运算；

d)更新二叉树存储模型，存储布尔差运算后的有效线段组群。

所述的更新二叉树存储模型，具体过程包括：

第一步：末层包围盒处理，具体为：

1.1)对于一个最末层小包围盒，取中心点，作为生成线的第一点，在对应的xy-zmin面上取第二点，这两点构成一条包围盒生成线；

1.2)计算包围盒生成线与工件面片组群的交线段，若交线段存在，则索引在生成线中；若交线不存在，则删除该包围盒；

1.3)重复步骤1.1和1.2，处理最末层所有小包围盒；

第二步：包围盒层次树二次处理，具体为：

2.1)从次最末层包围盒开始当任一包围盒的左右孩子结点均不存在，则删除该包围盒；

2.2)向上跳一层，再重复步骤2.1，直到更新完全部层次树，最终得到切削后的二叉树模型。

本发明涉及一种实现上述方法的系统，包括：用户界面模块、应用场景模块、设备管理模块和通讯中心模块，其中：用户界面模块与通信中心模块相连并传输系统本身的设置信息和仿真功能的调用信息，应用场景模块与通信中心模块相连并传输刀具和工件的模型调用和仿真运算数据信息，设备管理模块与通信中心模块相连并传输传感设备采集的刀具的实时位姿信息。技术效果

与现有技术相比，本发明基于二叉树的数据结构，对dexel改进模型的存储、搜索功能进行改进，大大优化了切削过程的实时仿真速度和精度控制。且该优化方法适用范围广，既能用于单向的dexel改进模型，也能用于二向和三向的dexel改进模型；本发明使用时间或位姿间隔极短的实际刀具位姿的集合，来近似替代刀具的包络体。这种方法可以适应任何刀具轨迹，适用范围广，特别是实时切削监控时无法事先确定刀具轨迹的情况；且每个位置的刀具模型与工件dexel改进模型之间的布尔运算方法，与刀具运动包络体的布尔运算方式相同，不增加计算复杂程度；还可通过控制多个孤立刀具位置的疏密程度，满足具体的仿真任务对精度和速度的个性化需求。

附图说明

图1为本发明流程图；

图2为实施例aabb包围盒示意图；

图3为实施例直线段组群示意图；

图4为实施例第一次分割示意图；

图5为实施例第二次分割示意图；

图6为实施例第三次分割示意图；

图7为实施例第n次分割示意图；

图8为实施例小包围盒示意图；

图9为实施例指针连接有效线段示意图；

图10为实施例二叉树结构示意图；

图11为实施例切削仿真过程中aabb包围盒示意图；

图12为实施例切削仿真过程中包围盒直线段示意图；

图13为实施例切削仿真过程中dexel模型示意图；

图14为实施例二叉树模型更新后示意图。

具体实施方式

本实施例具体包括以下步骤：

步骤1、建立刀具的几何仿真模型，具体为：使用时间或位姿间隔极短的多个孤立的刀具位姿的集合，来近似替代刀具的包络体。在仿真过程中，当已知刀具的初始几何模型和刀具位姿的实时传感信息后，即可仿真运算出每个孤立切削位姿的刀具几何仿真模型。

步骤2、在进行步骤1的同时，对工件进行进行dexel改进模型预处理，得到工件的dexel改进模型；单向dexel改进模型的建模方法，对于二向和三向的dexel改进模型同样适用，后者将xoy面上的z向单向dexel射线组群，推广为相互垂直的两向dexel射线组群、以及相互垂直的三向dexel射线组群中；整个切削仿真过程中，只需要进行一次dexel改进模型的预处理；本实施例以xoy面上的z向的单向dexel射线组群为例，介绍dexel改进模型的预处理的建模过程。具体步骤包括：

2.1)在工件的坐标系内，根据面片组群构造出工件的aabb包围盒，如图2所示，虚线线条即表示从xoz平面，沿着y向看到的包围盒。

2.2)在aabb包围盒内构建分别沿x、y、z三个轴向的直线段组群，该直线段组群由包围盒截取dexel射线组群而得到。如图3所示虚线线段为沿z向的直线段组群，其余两个方向也同样。

2.3)对3d包围盒的xoy面进行二叉空间分割得到2d包围盒，多个2d包围盒按照层次组成2d包围盒二叉树模型。

所述的二叉空间分割，以构造二叉树存储有效线段，构造时按照xoy面上的x向和y向进行二分法取直线，从而保证直线段与2d包围盒xoy面上的二叉分割树对应。

所述的二叉空间分割，通过以下方式得到：

第1步：确定最终分割尺度，即未来相邻生成线之间的间距值δ

第2步：对于包围盒的xy-zmin面，循环进行：校验x向长度和y向长度，对较长的一个进行一次分割，校验分割后获得小包围盒边长，并当两个边长都小于分割尺度值δ时停止分割。

所述的二叉空间分割，具体步骤包括：

i)第一次分割，对将xoy面上的矩形包围盒的长边进行分割，分为两个小矩形，为便于理解，标记为b1、b2，对应生成的二叉树如图4所示。

ii)第二次分割，对b1、b2矩形2d包围盒中的长边再分别进行分割。以b1为例，b1长边被分割的为c1、c2两个区域，对应生成的二叉树也在b1结点下增加c1和c2两个子节点，如图5所示。

iii)第三次分割，对第二次分割得到的四个矩形2d包围盒中的长边再分别进行分割。以c1为例，c1长边被分割的为d1、d2两个区域，对应生成的二叉树也在c1结点下增加d1和d2两个子节点，如图6所示。

iv)依此规律不断分割，直至第n次两个边长都小于分割尺度值δ时结束，此时对应的区域分割和二叉树如图7所示。

2.4)构造有效线段：取步骤2.3中获得的每末层小包围盒的中心点，作为生成射线在xoy面上的坐标，有效线段是由生成射线与工件面片组群求交后得到的线段，它代表工件一段实体。如图8所示，虚线为包围盒生成线，中心线为生成线的有效线段。对于一条生成线，可以存在0条或多条有效线段，如果有效线段为0条，说面该生成线与工件不相交，属于无效生成线，不再保留。重复此步骤，处理最末层所有小包围盒。

一条dexel射线上可能存在多条有效线段，根据z值的大小关系，将同一条dexel射线上的有效线段用指针依次连接，如图9所示。

每个连接的结点记录线id，以及一个横向相交线段的指针或id。将有效线段索引到二叉树中，如图10所示。

步骤3、根据刀具的几何仿真模型和工件的dexel改进模型进行切削过程仿真，计算有效线段，得到更新后的二叉树模型，具体过程包括：

3.1)在工件坐标系内，构造刀具的aabb包围盒，如图11虚线框所示

3.2)计算两个包围盒的重叠区域，即图12中阴影所示区域。根据重叠区域，以及三个方向的二叉树结构，确定与刀具相交的包围盒直线段。

3.3)生成切削后的有效线段并更新dexel模型。如图13所示，原始有效线段组l1为例，仅包含两个有效线段(p1,p1’)和(p2,p2’)，采用线段(p0,p0’)进行差运算，如下式所示：

(p1,p1’)u(p2,p2’)-(p0,p0’)＝(p1,p0)u(p2,p2’)。

运算后有效线段更新为(p1,p0)u(p2,p2’)。

3.4)更新二叉树模型如图14所示，判断最末层小包围盒中心点对应的有效线段，若有效线段存在，则不处理；若交线不存在，则删除该包围盒对应的二叉树结点。

3.5)二次更新二叉树模型，从次最末层包围盒开始，若某个包围盒的左右子结点均不存在，则删除此包围盒对应的结点；然后再向上跳一层，重复这个校验过程；直到更新完全部结点。

步骤4、根据更新后的工件的dexel改进模型进行仿真结果实时显示：使用marchingcubes算法，将dexel改进模型构造为三角面片显示模型，实现实时显示。

本方法与现有技术相比：

①本发明基于二叉树的数据结构，对dexel改进模型的存储、搜索功能进行改进，大大优化了切削过程的实时仿真速度和精度控制过程。且该优化方法适用范围广，既能用于单向的dexel改进模型，也能用于二向和三向的dexel改进模型。

②本发明使用时间或位姿间隔极短的实际刀具位姿的集合，来近似替代刀具的包络体。这种方法可以适应任何刀具轨迹，适用范围广，特别是实时切削监控时无法事先确定刀具轨迹的情况；且每个位置的刀具模型与工件dexel改进模型之间的布尔运算方法，与刀具运动包络体的布尔运算方式相同，不增加计算复杂程度；还可通过控制多个孤立刀具位置的疏密程度，满足具体的仿真任务对精度和速度的个性化需求。

上述具体实施可由本领域技术人员在不背离本发明原理和宗旨的前提下以不同的方式对其进行局部调整，本发明的保护范围以权利要求书为准且不由上述具体实施所限，在其范围内的各个实现方案均受本发明之约束。