一种考虑柔性节拍和操作人员技能差异的装配线平衡方法与流程

本发明属于装配线平衡技术领域，具体涉及一种考虑柔性节拍和操作人员技能差异的装配线平衡方法。

背景技术：

装配线平衡是指在实际生产情况的制约下，将一组具有紧前关系的工序分配给一定数量的工作站，使各工位的工时尽可能接近，以减少工位的时间浪费，提高生产线的整体效率。即便在工业发达的美国，每年也有5％-10％的时间浪费在平衡延迟中，因此，装配线平衡一直是制造业的重要问题。

1954年美国人bryton首次提出装配线平衡问题的概念。之后有关装配线平衡问题的研究方向主要是优化目标和求解方法。针对优化目标的不同，将装配生产线优化归为求工位最小化、生产节拍最小化和平滑指数最小化这三类问题。求解方法主要有数学解析法、启发式方法、工业工程方法、智能算法四种。但因为装配线平衡问题的约束条件往往是随着生产方式、生产条件的不同而发生改变，理论研究与实际生产的衔接存在困难，所以调节装配线平衡必须要考虑实际生产中的限制因素。

技术实现要素：

针对于上述现有技术的不足，本发明的目的在于提供一种考虑柔性节拍和操作人员技能差异的装配线平衡方法，以解决现有技术中在产线节拍变化和操作人员对同一工序加工时间不同的情况下不能合理划分工位的问题。

为达到上述目的，本发明采用的技术方案如下：

本发明的一种考虑柔性节拍和操作人员技能差异的装配线平衡方法，包括步骤如下：

1)调研装配线，分析工序的紧前逻辑关系，测定操作人员对于各工序的加工时间，根据订单需求确定装配线节拍；

2)定义装配线的参数，并建立求最少工位的数学模型；

3)利用遗传算法实现数学模型，对工序进行编码及种群初始化，染色体对应的是工序操作顺序，满足工序紧前关系；

4)基于染色体对应的工序操作顺序进行操作人员分配，一名操作人员对应一个工位，用蒙特卡洛方法求得一条染色体对应的工序操作顺序下工位数最少的分配方案；

5)对染色体进行选择、交叉、变异的遗传操作，得到新染色体对应的工序操作顺序的最少工位比原染色体更少时，则替代原染色体，否则重新进行遗传操作；

6)达到设定的最大遗传迭代次数后，输出工位数最少的工序操作顺序及操作人员分配方案；否则，转回步骤5)继续下一轮的遗传操作。

进一步地，所述步骤2)中的参数具体包括：工序总数n，工序编号i，i＝1,2,..,n；工序i的操作次序ji，ji＝1,2,..,n；工位总数q，工位编号k，k＝1,2,..,q；产线节拍ct；操作人员总数s，操作人员编号e，e＝1,2,..,s；操作人员-工序技能矩阵ts×n，该矩阵ts×n中的元素tei代表操作人员e加工工序i的平均时间；工序紧前关系矩阵mn×n，该矩阵mn×n中的元素mab：

操作人员-工序分配矩阵xs×n，该矩阵xs×n中的元素xei：

数学模型如下：

(21)目标函数：工位总数最小(被分配操作人员最少)：

(22)约束条件1：每个工序都要被分配，且只能分配一次：

(23)约束条件2：每个操作人员所在工位的节拍不能超过产线节拍：

(24)约束条件3：工序的分配顺序符合紧前逻辑关系：若k是l的紧前工序，即mkl＝1，则jk<jl；

(25)约束条件4：在一种工序操作顺序下，任意被分配给同一名操作人员的两个工序之间的工序也必须被分配给这名操作人员：

jk<jp<jl，若xek＝xel＝1，则xep＝1

其中，β是工序集合，φ是操作人员集合。

进一步地，所述步骤3)中编码方式为：按照工序的紧前逻辑关系，将工序排成一列作为一条染色体，每个工序对应染色体上的一个基因位。

进一步地，所述步骤4)中使用蒙特卡洛方法分配操作人员并求适应度过程如下：

(41)随机选取未被分配的操作人员e，从当前未分配的第一个工序i’开始，按照染色体对应的工序操作顺序依次向操作人员e分配，当分配了工序i”后，操作人员e负责的工序总时间t<＝ct；分配了工序i”+1后，t>ct；则当前操作人员e负责的工序为i’到i”；

(42)计算(41)中分配方案所需的操作人员数量，与上一轮的分配方案比较，操作人员数量少的记为当前最优；若达到设定的蒙特卡洛最大迭代次数，则输出当前启用操作人员最少的方案，人数越少，当前染色体的适应度值越高；否则转(41)。

进一步地，所述步骤5)具体包括：采用基于排名策略的轮盘赌方法进行选择操作；采用两点交叉法进行交叉操作；采用初始的编码方法进行变异操作。

进一步地，所述步骤5)中的选择操作如下：将同一代群体中的r种工序操作顺序按最少工位数从大到小排列，对于排名为d的操作顺序，其选择概率为：

生成(0,1]之间的随机数α，从群体中排名为1的个体开始，将其选择概率与后继个体的选择概率相加，直到累加和等于或大于α，则停止；其中最后加入的个体即为选择的工序操作顺序，重复上述操作直至达到种群规模。

进一步地，所述步骤5)中的交叉操作如下：使用两点交叉法，随机选择染色体中的两个基因位作为交叉点，将两条染色体交叉点之间的工序顺序互换，得到新的工序操作顺序。

进一步地，所述步骤5)中的变异操作如下：利用初始的编码方法生成一种新的工序操作顺序，按变异概率替代原有的工序操作顺序。

本发明的有益效果：

本发明考虑了实际生产中常见的柔性节拍和操作人员技能差异因素。现今企业多是按需生产，由订单需求决定产线节拍，可以保证不延期，也能防止提前完工导致的企业停工。面对不同的产线节拍，重新规划工位最少的方案，可以提高产线平衡，也节省了人力资源。操作人员对工序的不同加工时间决定各工位节拍，影响工位之间的节拍均衡，优化操作人员和工位之间的分配可以提升装配线平衡。因此本方法解决了在柔性节拍和操作人员的技能差异这两个因素影响下如何划分工位，以提高装配线平衡率。

附图说明

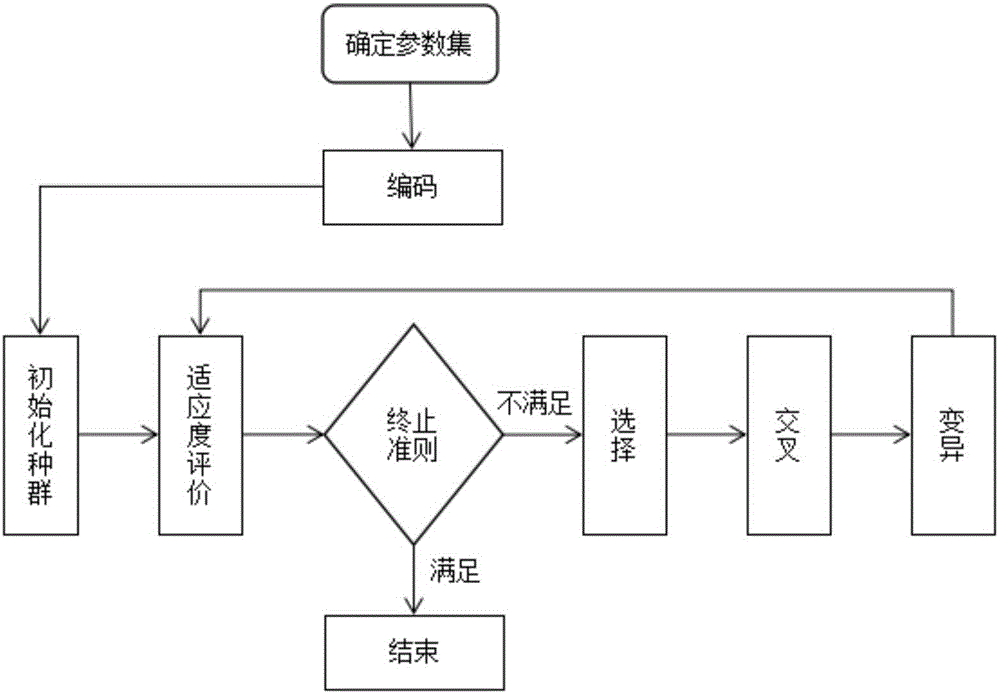
图1为本发明方法的流程图。

图2为某打印机厂pt板装配线的工序紧前逻辑关系图。

图3为某打印机厂pt板装配线上操作人员对各工序的操作平均时间示意图。

图4为通过本发明的计算后装配线工位划分和操作人员分配情况示意图。

图5为通过本发明的计算后装配线工位的山积图。

具体实施方式

为了便于本领域技术人员的理解，下面结合实例与示意图对本发明作进一步的说明，实施方式提及的内容并非对本发明的限定。

参照图1所示，本发明的一种考虑柔性节拍和操作人员技能差异的装配线平衡方法，以某打印机装配厂的pt板装配线平衡优化实例进行说明，包括以下步骤：

(1)对pt板装配线进行分析，该装配线包括23个工序，工序紧前逻辑关系图如图2，产线13名操作人员对每个工序的平均加工时间如图3，根据f企业最新一笔订单可以确定产线节拍ct＝40(秒)。

(2)定义参数并建立数学模型：工序总数n，工序编号i，i＝1,2,..,n；工序i的操作次序ji，ji＝1,2,..,n；工位总数q，工位编号k，k＝1,2,..,q；产线节拍ct；操作人员总数s，操作人员编号e，e＝1,2,..,s；操作人员-工序技能矩阵ts×n，该矩阵ts×n中的元素tei代表操作人员e加工工序i的平均时间；工序紧前关系矩阵mn×n，该矩阵mn×n中的元素mab：

操作人员-工序分配矩阵xs×n，该矩阵xs×n中的元素xei：

通过对装配线的分析可知：n＝23；s＝13；由图2可得工序紧前关系矩阵mn×n；由图3可得操作人员-工序技能矩阵ts×n。

数学模型如下：

(21)目标函数：工位总数最小(被分配操作人员最少)：

(22)约束条件1：每个工序都要被分配，且只能分配一次：

(23)约束条件2：每个操作人员所在工位的节拍不能超过产线节拍：

(24)约束条件3：工序的分配顺序符合紧前逻辑关系：若k是l的紧前工序，即mkl＝1，则jk<jl；

(25)约束条件4：在一种工序操作顺序下，任意被分配给同一名操作人员的两个工序之间的工序也必须被分配给这名操作人员：

jk<jp<jl，若xek＝xel＝1，则xep＝1

其中，β是工序集合，φ是操作人员集合。

(3)给工序进行自然数编号，按照工序的紧前关系，将工序排成一列作为一条染色体。以图2所示的工序紧前逻辑关系图为例安排工序组成一个染色体[1，5，11，3，8，9，2，12，13，6，7，14，10，4，16，17，18，19，20，21，22，23]，这个染色体表明第一次分配工序1，第二次分配工序5，第三次分配工序11…，最后一次分配工序23。

(31)按照上述规则生产染色体，达到预先设定的种群规模，完成初始化。

(32)适应度：用蒙特卡洛方法寻找每个染色体对应的使用操作人员最少的方案，按照染色体对应的工序操作顺序依次将工序分配给操作人员，一名操作人员负责一个工位，要求每个操作人员负责的工序总时间不得超过产线节拍。达到蒙特卡洛规定的最大迭代次数后即认为得到了当前染色体下工位最少的分配方式，工位数越少，染色体适应度越高。

(33)选择：将同一代种群中的r种工序操作顺序按最少工位数从大到小排列，对于排名为d的操作顺序，其选择概率为：

生成(0,1]之间的随机数α，从群体中排名为1的个体开始，将其选择概率与后继个体的选择概率相加，直到累加和等于或大于α，则停止；其中最后加入的个体即为选择的工序操作顺序，重复上述操作直至达到种群规模。

(34)交叉：按交叉概率选取被交叉的染色体。使用两点交叉法，随机选择染色体中的两个基因位作为交叉点，将两条染色体交叉点之间的工序顺序互换，得到新的工序操作顺序。以本例中的染色体为例：

父代1如表1，如下：

表1

父代2如表2，如下：

表2

若随机产生的交叉点为6和12，两个父代互相交换第6个到第12个基因位上的基因顺序，父代1中基因段[8，9，2，12，13，6，7]里的基因在父代2中的顺序是[7，6，13，12，2，9，8]，将此取代父代1中的原基因段。得到子代1如表3，如下：

表3

同理将父代2中的基因段[13，12，2，9，8，3，15]按照父代1中的顺序重组得到子代2如表4，如下：

表4

只有当子代适应度高于父代时，才会替代父代，否则重新进行交叉。

(35)变异：利用初始的编码方法生成一种新的工序操作顺序，按变异概率替代原有的工序操作顺序。若新工序操作顺序的最少工位数少于原工序操作顺序则替代，否则重新变异。

(36)终止准则：当达到遗传算法的最大迭代次数后，算法结束，输出当前启用操作人员最少的的工序操作顺序及操作人员分配方案。

本发明采用matlab编写算法求解程序，遗传算法的种群数目为20，交叉和变异的概率分别为0.8和0.2，最大迭代次数为100次。蒙特卡洛方法的最大迭代次数为10^5次。最后得到的工位划分和操作人员分配如图4，工位的山积图如图5。

可得现在的装配线一般来说，如果平衡率在85％以上，则属于“一件流”的制造模式。因此本发明的方法是有效可行的。

本发明具体应用途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进，这些改进也应视为本发明的保护范围。