一种估算金属增材制造超声冲击处理作用层深度的方法与流程

本发明涉及一种超声冲击处理作用层深度的方法，尤其涉及一种估算金属增材制造超声冲击处理作用层深度的方法，属于增材制造及超声冲击处理领域。

背景技术：

作为一种先进的制造技术，增材制造(additivemanufacturing,am)技术获得了广泛的应用。但是增材制造成形金属制件沉积态组织存在一些固有特征，以激光金属沉积(lasermetaldeposition,lmd)技术为例，由于成形过程由高能量密度激光束形成较小熔池，使送入熔池中的粉末完全熔化，冷却过程经历较高的温度梯度、极快的冷却速度以及大的凝固前沿生长速度，因此沉积组织多为发达的柱状枝晶、非平衡显微组织以及存在较大的残余应力。外延生长的柱状枝晶使沉积件力学性能各向异性。其次，局部快速凝固会在成形件中产生高的残余应力，若实验参数控制不当甚至会在晶间区域产生热裂纹，因此影响材料的疲劳强度和断裂韧性。力学性能各向异性以及较大残余应力的存在会限制激光沉积金属制件在高性能关键部件上的应用。

因此，为了消除激光金属沉积件组织不利特征，除了对成形工艺参数优化外，人们发展了多种辅助成形工艺技术，例如：后续热处理、表面冲击处理(smat)、滚压轧制、超声振动、热等静压、喷丸等来改善沉积件的组织和性能。但是这些技术存在各种各样的局限性，例如：超声振动技术不适合大尺寸构件的成形，因为随着构构件尺寸的增加，振动能场对零件上端熔池作用减弱，对换能器功率及负载能力提出更高要求；滚压轧制技术是采用滚轮对金属熔覆层进行逐层轧制锻造，把铸态组织变为锻造态组织，但需要对滚轮施加较大的压力，因此，这种技术难以成形薄壁件和形状复杂构件。后处理技术中热等静压及热处理技术等需要昂贵的大型设备且处理成本高，难以处理大型金属制件。

最近几年，超声冲击处理(ultrasonicimpacttreatment,uit)技术作为一种后处理技术因其设备小、操作简单、高能量密度输入等特点被广泛应用在焊接接头处理中，用来消除残余应力，降低表面应力集中，提高焊接接头的疲劳性能。在超声冲击处理过程中，普通正弦波电信号经过超声电源及换能器后，转化为20khz及以上超声频率振动信号，经变幅杆放大作用后，推动冲击针以较高速度冲击待处理材料表面，使冲击表面一定深度内发生严重的塑性变形以及改变材料表面的应力状态(由拉应力状态转化为压应力状态)，从而提高材料疲劳性能。后来人们结合金属增材制造(am)技术与超声冲击处理(uit)技术，发展了增锻复合制造技术。即在进行激光沉积金属的同时，施加超声冲击能量，实现“逐层沉积，逐层锻造”，可有效改善沉积层组织、锻合缺陷、消除内应力，其次，由于其冲击过程“小载荷，小冲击面积，大冲击能量密度”的特点，可实现较复杂薄壁金属零部件的复合成形。

为了制定合理的超声微锻造辅助增材制造成形工艺，需要估算每一层超声微锻造的作用深度。目前测定方法有金相观察、显微硬度测试法、ebsd位错密度测量等方法。金相观察方法需制备金相试样，需要经过系列砂纸打磨及抛光后通过金相显微镜才能观察到变形组织，而且此方法灵敏度低，只有在材料发生很大塑性变形后，才可以通过金相显微镜观察到变形组织，因此，由此观察得到的变形深度要远小于实际变形层深度；显微硬度测试方法操作简单，只需要沿被冲击试样深度方向上每隔一定距离(几十微米)进行显微硬度打点测试，如果材料发生塑性变形，由于材料的加工硬化效应可导致显微硬度上升，因此可侧面反映作用层深度。此方法较金相观察法操作简单且测量变形层深度范围更准确；ebsd方法可通过测量位错密度方法判断材料是否发生塑性变形，此方法测量最为精确，但是由于试样制备繁琐且测试费用非常昂贵，使用过程不方便。

因此，迫切需要提出一种简单的估算方法，用来获得特定的超声冲击处理工艺参数(频率、振幅等)下的作用层深度，以实现更方便、快捷的工程应用。此方法得到的作用层深度可用来指导激光金属沉积过程中逐层沉积层厚度以及线能量密度等参数的设定以获得较好“增锻”复合成形效果。因此，本专利提出了一个超声冲击处理作用层深度计算模型，用于准确估算超声微锻造作用层深度。

技术实现要素：

本发明的目的是为了预测在特定“增材”与“锻造”成形参数下作用层深度而提供一种估算金属增材制造超声冲击处理作用层深度的方法。

本发明的目的是这样实现的：

一种估算金属增材制造超声冲击处理作用层深度的方法，作用层深度计算模型为:

式中，rmax为作用层深度、υ为增材制造金属件泊松比、ρ为密度、e为弹性模量、f为超声换能器频率、a为变幅杆振幅、r0为冲击针半径、pin为冲击针、am为被冲击材料、σp0.2为被冲击材料在高应变率条件下的压缩屈服强度。

本发明还包括这样一些特征：

1.所述压缩屈服强度σp0.2替换为目标塑性应变下的应力σε，得到目标塑性应变条件下变形层深度；

2.所述方法适用激光金属沉积、激光熔丝沉积、电弧熔丝沉积或电子束熔丝堆积；

3.所述金属包括合金钢、不锈钢、钛合金、铝合金或高温合金。

本发明作用深度估算模型应用具体流程为：

(1)获得冲击针材料参数，包括密度、弹性模量。获得途径：①通过查阅相关标准或文献；②实际测量：密度测量可使用排水法；弹性模量可使用超声波法。冲击针尺寸半径可使用游标卡尺量出。

(2)获得被冲击材料参数，包括密度、弹性模量、泊松比、压缩屈服强度(uit条件下)。获得途径：①可通过查阅相关标准或文献；②实际测量：密度测量可使用排水法；弹性模量和泊松比可使用超声波法测量。压缩屈服强度可通过hopkinson压杆测试技术直接获得屈服强度(考虑hopkinson压杆测试应变率范围(10³～10⁴)和uit应变率范围相近)，亦可通过结合准静态压缩和hopkinson压杆测试技术求得材料动态硬化本构关系，进一步求得其在uit应变率范围下的屈服强度。

(3)设定超声冲击工艺参数，包括频率和振幅。此参数可通过调节超声冲击设备实现。

(4)把以上设定的超声冲击处理工艺参数及测量的相关材料参数代入作用深度预测模型，求得作用深度结果。

(5)根据步骤(4)求得的作用深度结果，用来指导实际增材质制造过程工艺参数的设定，比如线能量输入密度，单层沉积层高度增量，材料送给速度等，使估算作用层深度大于实际单层沉积厚度，使增锻复合制造达到较好成形效果，实现较高的力学性能。

亦可通过把模型中屈服强度σp0.2替换为目标塑性应变条件下的应力σε，此应力可通过被处理材料的动态硬化本构方程求得，求得被冲击材料塑性应变不小于目标应变ε的变形层深度，达到更好的锻造效果。

与现有技术相比，本发明的有益效果是：

本发明的估算方法可以用来预测在特定“增材”与“锻造”成形参数下作用层深度，用于指导“超声波辅助增材制造”复合制造成形工艺制定，如逐层沉积层高度、线能量输入密度、uit频率及振幅等，实现增材制造金属零部件组织和内应力的准确控制，解决现有增材制造技术成形金属构件控形、控性难题，获得和锻件性能相媲美的高性能金属零部件；此估算方法适用于几乎所有增材制造方法如激光金属沉积、电弧熔丝沉积、电子束熔丝沉积等；以及几乎所有可用于增材制造成形的金属材料如不锈钢、铝合金、钛合金等；超声冲击作用层深度的估算，具有很好的精度。

附图说明

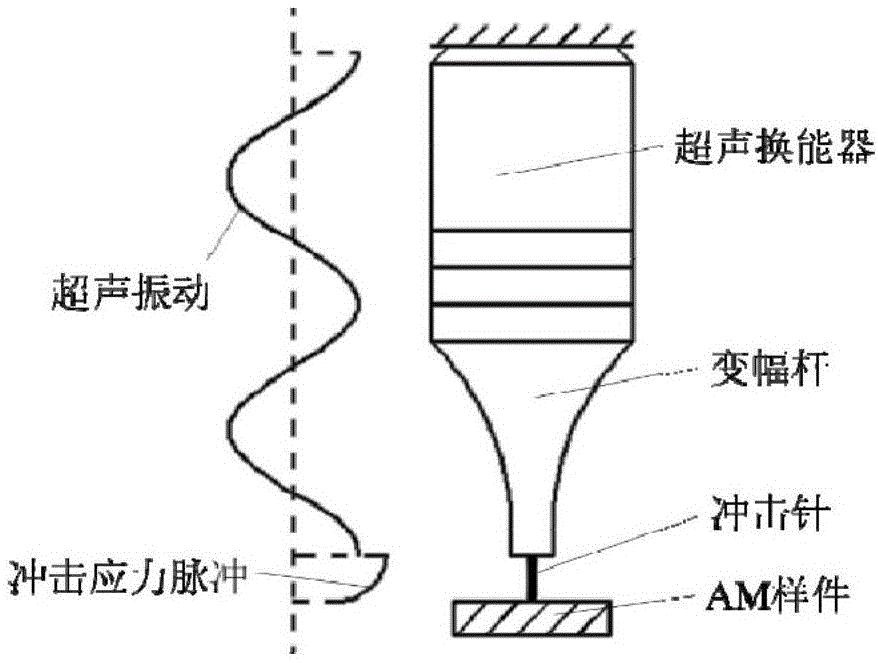
图1是超声冲击处理原理图；

图2是应力波在半球形冲击针端部传播示意图；

图3a是材料应力-应变曲线图；

图3b是材料应力-速度曲线图；

图4是超声冲击处理弹塑性腔扩张模型；

图5是显微硬度分布曲线；

图6是本发明作用深度估算模型应用流程图。

具体实施方式

下面结合附图与具体实施方式对本发明作进一步详细描述。

本发明提出一种估算方法，用来计算增材制造金属制件在超声冲击处理过程中形成的应力场以及作用层深度。此得到的计算模型可以用来预测在特定“增材”与“锻造”成形参数下作用层深度，此计算模型可用于指导“增锻”复合制造成形工艺制定，实现增材制造金属制件组织和内应力控制。

图1是超声冲击处理原理图。超声冲击设备相关参数可给出为：超声换能器振动频率f＝20khz、变幅杆端振幅a＝80μm、超声振动周期为冲击针端部为半球形且半径r0＝2.6mm。

推导过程分四部分进行：冲击针端部冲击速度的计算、冲击点处应力分析、超声冲击作用深度计算以及计算模型验证。

冲击针端部速度计算：冲击针材料一般使用高强钢，假定超声冲击处理过程中冲击针没有发生塑性变形而一直保持为弹性状态。冲击针速度随变幅杆振动周期的不同时刻而变化的但存在一个最大值。变幅杆端远大于冲击针直径，因此可认为冲击针在接触面上位移和速度跟随变幅杆端相关参数变化。变幅杆端质点振动最大速度为：

vinimax＝2πfa(1)

假定应力波在冲击针内传播满足一维应力波理论，当应力波波阵面由圆柱部分传播到半球形端部时，由于传播介质横截面积的改变，应力波强度也会发生变化。

图2所示为应力波在半球形冲击针端部传播示意图，物理量如质点速度、应力等是位置和时间的函数。忽略应力波在半球形端部传播时间，现研究在特定时刻下，冲击针端部质点速度场。假定冲击针初始状态为静止和无应力状态。当δh非常小，考虑到应力波在传播介质不同截面处的反射和透射定律：

vt(h+δh)＝n(h)·t(h)·vt(h)(2a)

s(h)＝π·r(h)²＝π·(r0²-h²)(2d)

式中，vt为冲击针前端质点速度；(ρcs)是广义波阻抗，其中ρ，c，s为别为材料密度、应力波速和横截面面积；t为透射系数；n为波阻抗比。因此：

初始边界条件为：

vt(0)max＝2πfa，r(0)＝r0(4)

联合初始边界条件，解以上速度场微分方程，速度场可以解得：

此处所述的速度场只是描述波阵面上质点速度在传播过程中的增长规律，并非代表冲击针前端特定时刻整个区域的速度分布。真实冲击过程中，冲击针尖前端一定区域内会发生塑性变形。假定前端发生塑性变形后近似为一个平面且半径为rtip，根据应力波在自由端反射定律，冲击针前端速度可以计算为：

冲击点处应力分析：冲击针以一定速度冲击待处理材料表面，冲击点(实际为一个较小的面)处应力及后续被冲击材料发生塑性变形需依次分析。

假定增材制造金属试件在特定应变率条件下满足线性硬化材料模型，图3a为增材制造试样应力-应变曲线简图。被处理材料在uit作用下经历两个阶段：弹性阶段和塑性变形阶段。在uit过程中，冲击针以每秒几百赫兹频率冲击试件表面，因此，同一个区域经历重复多次冲击，由冲击过程质点应力-速度关系，被冲击材料不断发生加工硬化。随着冲击次数的增加，冲击应力演化如图3b质点应力-速度曲线所示。当冲击次数趋向于无穷大时，质点应力和速度存在极限值，使得：

σimpmax＝-[(ρc)e]am·vimpmin＝[(ρc)e]pin·(vimpmin-vtipmax)(7)

式中，σimpmax，vimpmin分别为冲击点处质点可达到的极限应力和速度。σimpmax可求得：

冲击点处最大冲击应力可通过式(8a)得到，其值大于初始屈服强度σp0.2。此求得的冲击点处最大应力在可作为后续塑性变形场的初始边界条件进一步求得塑性变形区深度。

超声冲击作用层深度计算：当冲击针端部以较小的接触面积作用于待冲击材料表面，可近似认为冲击效果以球形应力波在被冲击材料内传播，因此在分析uit作用区域时基于弹塑性腔扩张模型，如图4所示。随着高频重复冲击过程进行，球形应力波在传播过程中，塑性区材料不断经历着应变硬化及重新加载过程。uit作用区域被分为3个部分：核心区、塑性变形区、应力释放区。由于塑性变形区深度是衡量冲击效果最重要的指标(前面背景技术已分析)，此专利主要得到一个计算模型用来预测塑性变形区深度。假设待冲击材料冲击前状态为静止和无应力状态。考虑到影响区内质点运动对称性，基于质量守恒、动量守恒、本构关系及波阵面上相容条件，球形应力场沿特征线方向满足关系：

假定塑性变形区初始边界(核心区终止边界)面积和冲击针端面积相等，因此，应力场边界条件为：

由弹性波速和弹性模量的关系：

结合应力微分方程(式9)以及应力场边界条件(式10)，冲击应力场可以解得：

此处所述的应力场只是描述波阵面上应力在传播过程中的衰减规律，并非代表特定时刻整个冲击影响区内的应力分布。球形应力波传播过程中应力逐渐减弱且应力单元体处在三向压应力状态。随球形波传播距离的增加，存在一个临界半径，在此半径上，应力减小到被冲击材料的屈服强度，此后塑性变形终止。采用mises和tresca屈服准则作为屈服条件的判定，两准则在此uit过程中有相同的表达形式：

σr-σθ＝σp0.2(13)

将uit处理过程应力场代入屈服准则：

因此，作用层(塑性变形区)最大深度可以求得：

式中：

f为超声换能器频率、a为变幅杆振幅、r0为冲击针半径、ρ、e分别为增材制造金属件和冲击针密度、弹性模量(以下标区分)、υ为增材制造金属件泊松比、σp0.2为被冲击材料在高应变率(uit应变率)条件下的压缩屈服强度(公式中取负值)。

此计算模型适用于几乎所有增材制造方法(如激光金属沉积、电弧熔丝沉积、电子束熔丝沉积等)以及几乎所有可用于增材制造成形的金属材料(如不锈钢、铝合金、钛合金等)。可用来指导实际增锻复合成形过程中复合成形参数的设定，可以预测在特定uit参数下(功率、振幅等)，材料作用层深度。

具体实施例1：

采用激光金属沉积(lmd)方法，制备了316l不锈钢试样(lmd-deposited316lss)，并后续进行超声冲击处理(uit)实验，用来验证塑性区深度计算模型的正确性。超声冲击实验参数为：超声频率20khz,变幅杆振幅80μm，冲击针半径2.6mm。冲击针使用高强钢，其密度和弹性模量分别为7.85g/cm³和205gpa。由式(15a)，为了计算作用层深度，需要获得的待冲击材料参数有密度、弹性模量、泊松比及高应变率条件下材料屈服强度。排水法测得lmd-deposited316lss密度为7.75g/cm³。弹性模量、泊松比可通过超声波法测得，其值分别为200gpa和0.3。考虑lmd成形材料组织和性能不同于锻造状态，其在高应变率条件下的屈服强度和本构关系缺少统一标准，因此，本专利采用准静态和动态压缩实验，获得沉积材料在不同应变率条件下的本构关系。考虑到uit相对较高的冲击速度及大塑性变形，本方法采用johnson-cook(jc)非线性硬化材料模型，此模型综合考虑了应变硬化、应变率硬化及温度软化效应。由于uit实验在室温下进行及冲击处理过程中材料发生有限的温升，温度软化效应可忽略不计。准静态压缩测试通过万能试验机对压缩试样测试，测试应变率为10^-3/s。动态压缩测试可通过分离式霍普金森压杆(shpb)测试技术进行测试，应变率范围为10³～10⁴/s。通过对准静态及动态压缩应力-应变数据进行对数拟合(转化为直线拟合)，可得到lmd-deposited316lss的jc本构关系：

通过本构关系(式16)，可获得lmd-deposited316lss在特定应变率条件下的屈服强度和应变硬化率。假定uit过程中，沉积材料的应变率范围为[10³,10⁴]，得到屈服强度限制在较小的范围[590mpa,610mpa]，取σp0.2＝600mpa。把以上实验参数和材料参数代入作用区深度计算模型(式15a)，可得作用层深度：rmax＝0.71mm。

本实验采用显微硬度测试法标定lmd-deposited316lss试样在超声冲击处理后作用层深度。图5为显微硬度沿深度方向分布图，由显微硬度分布拟合曲线交点，发现距表层深度0.81mm内显微硬度发生较为明显的升高。因此，可以认为uit后作用层深度为0.81mm。

对比作用层预测结果(0.71mm)和实际测量结果(0.81mm)，发现计算结果略小于实际测量结果，可能原因是：

(1)真实冲击过程冲击针满足冲击-回弹-冲击模型，而在理论计算中，因为冲击针回弹速度不容易测量而假定冲击针初始为静止和无应力状态，因此，实际变形层深度要比理论计算结果高一些；

(2)应力叠加(stresssuperposition)效应在uit过程不能忽略。uit处理过程中，材料内部会发生应力波反射、透射及叠加效应，因此有些局部区域会产生高压应力区，促进材料发生塑性变形，导致实际变形层深度要比理论计算结果高一些；

(3)超声软化(softeningeffect)效应促进被冲击材料发生塑性变形。有学者研究发现，uit处理过程中，超声能量容易被位错吸收，促进位错滑移和攀移，减小材料屈服强度，提高作用层深度，导致实际变形层深度要比理论计算结果高一些。

(4)uit处理过程中材料表面经受高应变及高应变率变形，产生大量塑性变形热，当产生的热量无法立即被导出，导致被冲击部位产生一定温升，减小材料的屈服强度，因此有助于扩大塑性变形区作用深度。

若在理论计算模型中把以上因素考虑在内，将有助于减小理论计算模型和实验测量间的误差。因此，此分析证明了作用层深度计算模型的正确性。

具体实施例2：

采用激光金属沉积技术制备了304不锈钢，并后续进行超声冲击处理(uit)实验。超声频率20khz，变幅杆振幅80μm，冲击针半径2.6mm。冲击针使用高强钢，其密度和弹性模量分别为7.85g/cm³和205gpa。激光沉积304不锈钢材料参数为：密度7.80g/cm³,弹性模量和泊松比分别为201gpa和0.3，动态本构关系为：

因此其uit过程中压缩屈服强度为300mpa。把以上实验参数和材料参数代入作用区深度计算模型(式15a)，可得作用层深度：rmax＝1.41mm。同样采用显微硬度分布测试，测得其实际作用区深度为1.60mm。其结果在误差允许范围内，因此进一步验证了此作用深度估算模型的正确性。

综上所述：本发明提出一种估算方法，用来计算增材制造金属零部件在超声冲击处理过程中形成的作用层深度。此得到的估算方法可以用来预测在特定“增材”与“锻造”成形参数下作用层深度，用于指导“超声波辅助增材制造”复合制造成形工艺制定(如逐层沉积层高度、线能量输入密度、uit频率及振幅等)，实现增材制造金属零部件组织和内应力的准确控制，解决现有增材制造技术成形金属构件控形、控性难题，获得和锻件性能相媲美的高性能金属零部件。此计算方法适用于几乎所有增材制造方法(激光金属沉积、电弧熔丝沉积、电子束熔丝沉积等)以及几乎所有可用于增材制造成形的金属材料(不锈钢、铝合金、钛合金等)超声冲击作用层深度的估算，具有很好的精度。