弧齿锥齿轮含安装误差的齿面载荷传动误差数值计算方法与流程

本发明属于弧齿锥齿轮设计领域，具体为一种弧齿锥齿轮含安装误差的齿面载荷传动误差数值计算方法。

背景技术：

弧齿锥齿轮传动是机械工程等领域最常见、最普遍的传动形式之一，由于具有承载能力大、传动平稳、传动噪声低、传动比大、重合度高等特点，可以高效率、高可靠的传递空间内任意轴间的运动和力。而弧齿锥齿轮的传动误差作为弧齿锥齿轮齿面接触性能的评价标准之一，其与弧齿锥齿轮的冲击、振动、噪音等息息相关，直接影响着弧齿锥齿轮的运转平稳性。

为了得到优良的传动误差幅值以及传动误差曲线，必须考虑安装误差，齿形误差等多种误差对传动误差的影响。对于弧齿锥齿轮的传动误差计算，目前主要采用齿面接触分析求解不加载情况下的传动误差以及利用有限元方法求解加载条件下的传动误差，都存在人为的偶然性和不确定性。

技术实现要素：

本发明的目的在于提供一种能保证求解过程确定不存在人为影响的弧齿锥齿轮含误差的齿面载荷传动误差数值计算方法。

本发明提供的这种弧齿锥齿轮齿面载荷传动误差数值计算方法，分别计算单齿啮合不加载、加载和双齿啮合不加载、加载状态下考虑安装误差的传动误差，从而分别得出单齿啮合载荷传动误差和双齿啮合载荷转动误差，包括以下步骤：

a、传动误差定义

传动误差表示的是在啮合转动过程中，从动轮的实际转角相对于理论转角的差值，即传动误差为：

其中，φ1为小轮的转角；φ2为大轮的转角；n1和n2分别为小轮和大轮的齿数，小轮为主动轮、大轮为从动轮；

b、单齿啮合不加载状态下的传动误差δφ1计算

b.1)输入机床调整卡参数、基本齿坯设计参数和刀具参数，通过齿面参数化建模，确定大、小齿轮的啮合接触状态以及坐标转换矩阵，大轮考虑安装误差的坐标转换矩阵，求解大、小齿轮精确的齿面初始点；

b.2)根据点矢重合、法矢重合以及啮合条件建立啮合接触非线性方程组(tca方程组)；

b.3)计算大轮理论转角，求解大轮实际转角，计算传动误差，求得未知参数；

b.4)改变小轮转角，重复步骤2.2)和2.3)，如此循环迭代，直至求出在所需转角之下的大轮实际转角，即可计算出δφ1；

c、单齿啮合加载状态下，由于受载变形引起的传动误差δ1^*计算

c.1)求解齿面上接触点k到旋转轴线的距离rk、齿面主曲率δk和接触点k的螺旋角βk和齿面接触力f；

c.2)根据主曲率δk和齿面接触力f计算齿面接触椭圆的长半轴a、短半轴b及以及齿面变形量w；

c.3)根据上述求解得出的参数，求解在载荷作用下引起的传动误差△1^*；

单齿啮合载荷状态下的传动误差

d、双齿啮合不加载状态下的传动误差计算过程和原理与单齿啮合不加载状态下的计算一样；

e、双齿啮合加载状态下，两齿对由于受载变形引起的的传动误差计算

e.1)先根据输入参数确定其中一个齿对0的啮合接触状态和坐标转换矩阵，求解初始点，并建立tca方程组；

e.2)再将齿对0通过坐标变换绕自身轴线旋转一个齿的角度得到齿对1，重新根据输入参数确定其啮合接触状态和坐标变换矩阵，建立tca方程组；

e.3)根据建立的方程组求解方程中所涉及的未知参数变量，包括大轮实际转角和小轮实际转角；

e.4)基于求得的大轮实际转角和小轮实际转角，利用单齿啮合不加载计算时的公式计算得出双齿啮合两齿对的不加载传动误差；

e.5)根据齿对0的tca方程组，求解齿面主曲率δk0、接触点螺旋角βk0、接触点到轴线距离rk0和由于受载变形引起的传动误差ste0；根据齿对1的tca方程组，求解齿面主曲率δk1、接触点螺旋角βk1、接触点到轴线距离rk1和由于受载变形引起的传动误差ste1；

e.6)利用步骤(e.5)计算出的参数，建立传动误差相等和载荷平衡方程，分别计算出两个啮合齿对上的齿面接触力f0和f1，回代求解可得双齿啮合加载状态下两啮合齿对引起的传动误差；

单齿啮合不加载传动误差δφ1的具体计算如下：

设定与切齿机床刚性固接的机床坐标系sg，与轮坯刚性固接的轮坏坐标系s1，与摇台刚性固接的坐标系st；在机床固定坐标系下加工弧齿锥齿轮的刀盘齿面是一个圆锥面，其方程可表示为：

对应的刀盘单位法矢为：

其中，(up，θp)是曲面坐标，α是刀具的齿形角，rc是刀盘半径，具有正α和负α的矢量函数分别表示用于加工小轮凹面和凸面的两个刀盘的齿面；

首先，大、小轮在各自的坐标系下建立齿面模型，从刀盘到轮坯的转换矩阵：

其中，φ1＝mcφc1，mc为切削滚比；γm1，δem1，δxb1，δxd2，sr1，q1均为机床调整参数，均可通过机床调整卡得到；φc1是摇台的转角。

为了后续的法线矢量计算，将转换矩阵去掉最后一行和最后一列得到它的子矩阵：

从轮坯坐标系到啮合坐标系的转换矩阵为：

式中，旋转角度

旋转位移(△l)1＝((△lx)1,(△ly)1,(△lz)1)；

它对应的子矩阵为：

到达同一啮合坐标系后，由于安装误差的存在，两齿面可能没有发生点接触，需考虑安装误差进一步旋转变换；将安装误差加到大轮的齿面上，小轮保持不变，大轮考虑安装误差的坐标变换矩阵为:

它对应的子矩阵为：

这里，et为两齿轮轴线之间夹角的安装误差；eax为沿着齿轮轴线方向的安装误差；eos为齿轮轴间距安装误差；

经过整个坐标变换之后，小轮在啮合坐标系下的齿面方程和法线矢量可表示为：

rm1(θ1,φ1)＝(mt-f)1×m1p·rp(θ1,φ1)(10)

nm1(θ1,φ1)＝(lt-f)1×l1p·np(θ1,φ1)(11)

将安装误差加入大轮齿面，通过所有坐标变换后，可得大轮齿面在啮合坐标系下的齿面方程和齿面法矢：

rm2(θ2,φ2)＝mm-a×(mt-f)2×m2p·rp(θ2,φ2)(12)

nm2(θ2,φ2)＝lm-a(lt-f)2×l2p·np(θ2,φ2)(13)

根据上述两式可求解小轮齿面的第一和第二基本齐式；

第一基本齐式：

第二基本齐式：

式中，rθ1和rφ1分别为齿面的两条切线；

将求得齿面的第一和第二基本齐式代入以下方程可解得齿面的主曲率rk1和rk2；

同理，可求得大轮在啮合坐标系下的齿面方程rm2和法线矢量nm2，以及大轮齿面的主曲率；

两齿面要达到啮合传动，接触曲面必须处于连续切触状态，要求两齿面的矢量和法矢在任一瞬时都重合，且满足啮合方程；

nm1(θp,φc1)＝nm2(θg,φc2)(19)

rm1(up,θp,φc1)＝rm2(ug,θg,φc2)(20)

从上述两个矢量方程可以导出含有六个未知数up，θp，φc1，ug，θg，φc2的五个独立的矢量方程；要想求解未知参数，必须加上啮合方程作为补充，啮合方程可表示为：

n·v＝nm1(θp,φc1)·v12＝f(up,θp,φc1)＝0(21)

式中，v12是相对运动速度；

这里

综合以上六个非线性方程组成的方程组，可以求解上述六个未知参数(up，θp，φc1，ug，θg，φc2)；

为求解传动误差，需给小轮一个初始转角，每一个转角，进行一次齿面接触分析(求解tca方程组)，得到一组参数，通过多次迭代，接触分析求解可得一系列大轮轮的实际转角和理论转角，大轮的实际转角减去理论转角可以得到齿轮在不加载情况下的传动误差δφ1。

单齿啮合加载状态下引起的传动误差δ1^*计算具体如下：

根据齿轮所受的弯矩可计算齿面上所受的力:

式中，m是齿轮所受的弯矩；rk是齿面接触点k到齿轮旋转轴之间的距离，可由公式计算；α是刀具齿形角；βk是齿面接触点k的螺旋角；由于小轮的旋转轴为z轴，可得齿面接触点k到z轴的距离为：

接触点k位置的螺旋角可由公式求出：

式中，r0为刀盘半径；r′为接触点k处的锥距；β为名义螺旋角；r为中点锥距；r0为外锥距；b为齿宽；

根据上述求解的齿面上所受的力和齿面的主曲率可以计算齿面接触椭圆的长半轴长以及齿面变形：

长半轴：

短半轴：b＝λa(32)

式中，λ为方程(33)的根：

δk2j1(λ)-δk1j2(λ)＝0(33)

齿面变形量：

其中，e1、e2分别为小大轮的弹性模量；u1、u2分别为小大轮的泊松比；e^*是综合弹性模量，ξ为通用加工参数刀转角；

至此，齿面变形w，接触椭圆长轴长a，齿面任意一点螺旋角βk，齿面任意一点到旋转轴线的距离rk参数都已经求出；综合以上所求的参数，可以计算齿面在受载情况下的传动误差：

整个求解过程可以利用数值计算辅助软件实现。

步骤5.6)建立的传动误差相等和载荷平衡方程为：

δφ0(f0)＝δφ1(f1)(40)

f0rk0cosαcosβ0+f1rk1cosαcosβ1＝m(41)。

本发明在齿面接触分析的基础上求解弧齿锥齿轮在加载和不加载条件下的齿面传动误差，且在求解过程中考虑了安装误差对传动误差的影响，能保证两齿面之间真正发生点接触。为弧齿锥齿轮的设计与分析提供有意义的思路。整个求解过程均可利用数值计算辅助软件予以实现，不存在人为因素导致的偶然性和不确定性，计算过程可通过软件实现。

附图说明

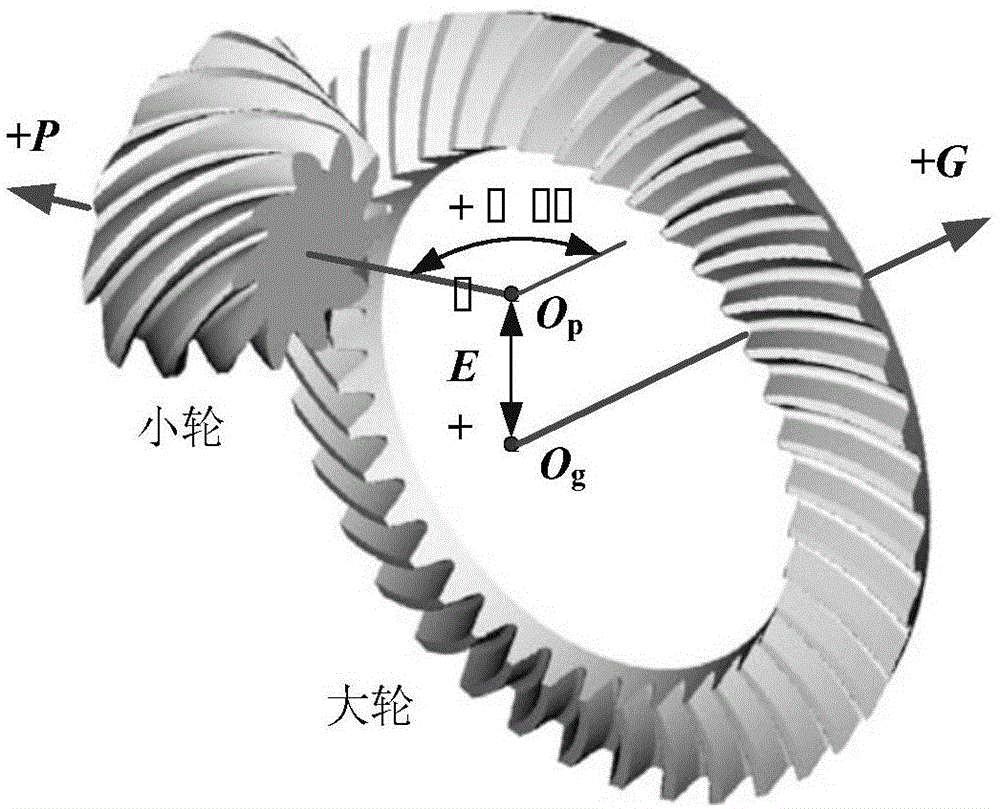
图1为弧齿锥齿轮制造装配示意图。

图2为考虑安装误差情况下单齿啮合传动误差求解流程图。

图3为考虑安装误差情况下双齿啮合传动误差求解流程图。

图4为本发明一个算例单齿啮合时不加载传动误差曲线图。

图5为本算例单齿啮合时加载传动误差曲线图。

图6为本算例双齿啮合时加载传动误差曲线图。

具体实施方式

本发明不同于传统的传动误差计算方法，提出了一种考虑安装误差的弧齿锥齿轮加载传动误差数值计算方法，利用本方法分别对安驰啮合状态和双齿啮合状态下的传动误差进行数值计算，具体如下：

传动误差表示的是在啮合转动过程中，从动轮的实际转角相对于理论转角的差值。即传动误差为：

其中，φ1为小轮的转角；φ2为大轮的转角；n1和n2分别为小轮和大轮的齿数。

需要说明的是，由于小轮的建模加工过程相对于大轮来说都是较为复杂的，所以本发明的加工分析过程主要以小轮为主，大轮的计算求解可参考小轮的方法和过程。

一、关于单齿啮合下的传动误差计算

在机床固定坐标系下加工弧齿锥齿轮的刀盘齿面是一个圆锥面，其方程可表示为：

对应的刀盘单位法矢为：

其中，(up，θp)是曲面坐标，α是刀具的斜角，rc是刀盘半径，具有正α和负α的矢量函数分别表示用于加工小轮凹面和凸面的两个刀盘的齿面。

通过相应的坐标变换将机床固定坐标系下的刀盘方程转化到轮坯坐标系下，得到轮坯坐标系下的齿面方程，本发明所用的从机床坐标系到轮坯坐标系的转换矩阵为：

其中，φ1＝mcφc1，mc为切削滚比，φc1是摇台的转角。γm1，δem1，δxd2，sr1，q1，δeb1均为机床调整参数，均可通过机床调整卡得到。

为了后续齿面法向量计算，需将转换矩阵去掉最后一行和最后一列，得到其对应的子矩阵：

两齿轮要实现啮合，必须旋转一定的角度到达同一齿面啮合坐标系，将齿面坐标系下的齿面方程和齿面单位法向矢量转换到啮合坐标系下，得到啮合坐标系下的齿面方程rm1(θ1,φ1)和齿面法向矢量nm1(θ1,φ1)。文中所用的从轮坯坐标系到啮合坐标系的转换矩阵为：

式中，旋转角度旋转位移(△l)1＝((△lx)1,(△ly)1,(△lz)1)。

它对应的子矩阵为：

到达同一啮合坐标系后，由于安装误差的存在，两齿面可能没有发生点接触，需将安装误差也考虑进去，进一步旋转变换。

需要说明的是，考虑安装误差时，一般只需将安装误差加到其中一个齿面上考虑即可，本文所用的方法是将安装误差加到大轮的齿面上，小轮保持不变。其考虑安装误差的坐标变换矩阵为：

它对应的子矩阵为：

式中，et为两齿轮轴线之间夹角的安装误差，即图1中的α；eax为沿着齿轮轴线方向的安装误差，即图1中的p和g；eos为齿轮轴间距安装误差，即图1中的e。

经过整个坐标变换之后，小轮齿面在啮合坐标系下的齿面方程和齿面法矢可表示为：

rm1(θ1,φ1)＝(mt-f)1×m1p·rp(θ1,φ1)(10)

nm1(θ1,φ1)＝(lt-f)1×l1p·np(θ1,φ1)(11)

将安装误差加入大轮齿面之后，通过所有坐标变换后，可得大轮齿面在啮合坐标系下的齿面方程和齿面法矢：

rm2(θ2,φ2)＝mm-a×(mt-f)2×m2p·rp(θ2,φ2)(12)

nm2(θ2,φ2)＝lm-a(lt-f)2×l2p·np(θ2,φ2)(13)

根据上述两式可求解小轮齿面的第一和第二基本齐式。

第一基本齐式：

第二基本齐式：

式中，rθ1和rφ1分别为齿面的两条切线。

将求得齿面的第一和第二基本齐式代入以下方程可解得齿面的主曲率rk1和rk2；

同理，可求得大轮在啮合坐标系下的齿面方程rm2和法线矢量nm2，以及大轮齿面的主曲率；

齿面要达到啮合，接触曲面必须处于连续切触状态，要求两齿面的位置矢量和法线矢量在任一瞬时都重合，并且两齿面满足啮合原理方程。

nm1(θp,φc1)＝nm2(θg,φc2)(19)

rm1(up,θp,φc1)＝rm2(ug,θg,φc2)(20)

n·v＝nm1(θp,φc1)·v12＝f(up,θp,φc1)＝0(21)

式中，v12是相对运动速度。

其中，

根据以上方程组可以导出六个有效的方程，求解可得六个未知参数up，θp，φp，ug，θg，φg。根据上述求解的六个参数，可以求得齿面上任意一点的主曲率δk1和δk2。

为求解传动误差，需给小轮一个初始转角，每一个转角，进行一次齿面接触分析，得到一组参数，通过多次迭代，接触分析求解可得一系列大轮的实际转角和理论转角，大轮的实际转角减去理论转角可以得到齿轮在不加载情况下的传动误差δφ。其大致的求解流程如图2所示。

为考虑载荷因素的影响，必须计算齿面由于受载变形引起的传动误差δ*。由齿轮所受的载荷可计算齿面上的接触力：

其中，m是齿轮所受的弯矩；rk是齿面接触点k到齿轮旋转轴之间的距离；α是刀具齿形角；βk是齿面接触点k的螺旋角。

由于小轮的旋转轴为z轴，可得齿面接触点k到z轴的距离为：

式中，r0为刀盘半径；r′为接触点k处的锥距；β为名义螺旋角；r为中点锥距。r0为外锥距；b为齿宽。

综合上述求解的齿面接触力和齿面的主曲率，通过公式可计算齿面接触椭圆的长半轴和短半轴：

长半轴：

短半轴：b＝λa(32)

式中，λ为方程(34)的根：

δk2j1(λ)-δk1j2(λ)＝0(33)

齿面变形量：

其中，e^*是综合弹性模量；e1、e2分别为小大轮的弹性模量；u1、u2分别为小大轮的泊松比。

至此，齿面变形，齿面接触力，齿面接触椭圆长半轴，齿面一点螺旋角，齿面一点到齿轮旋转轴线的距离等参数都已经求出，根据求解的参数可以计算齿轮在载荷作用下的传动误差：

上述整个求解过程均可以利用数值计算辅助软件予以实现。结合上述求得的不加载条件下的传动误差δφ和加载情况下的传动误差δ^*，得到弧齿锥齿轮在载荷作用下的传动误差：

δφ＝△φ+△^*

二、关于双齿啮合下的传动误差计算

双齿啮合下的传动误差由不加载状态下的传动误差和加载条件下的传动误差两部分组成，其中不加载条件下的传动误差计算过程和原理与单齿啮合下的计算一样。具体流程可参看单齿啮合状态下的传动误差的计算过程。关于加载条件下的传动误差的计算，与单齿啮合不同的是，双齿啮合时，有两对齿(齿对0和齿对1)共同承担总的扭矩，需要分别计算各自齿面上的齿面接触力。如图3所示，大致计算流程如下：

a)先依据单齿啮合计算方法，求解齿对0上的接触点螺旋角βk0，接触点到齿轮旋转轴线的距离rk0，以及传动误差δ0^*等参数。

b)再对齿对1进行同样的计算分析，得到齿对1上接触点螺旋角βk1，接触点到齿轮旋转轴线的距离rk1，以及传动误差δ1^*等参数。

c)利用上述参数，根据传动误差相等和载荷平衡关系建立方程，得到双齿接触时，两对齿面上各自的齿面接触力f0和f1，回代入方程(28)和(34)，即可求得在加载条件下，弧齿锥齿轮双齿啮合的传动误差。

δφ0(f0)＝δφ1(f1)(40)

f0rk0cosαcosβ0+f1rk1cosαcosβ1＝m(41)

d)综合双齿啮合下的不加载与加载两种状态下的传动误差，可以得到弧齿锥齿

轮在双齿啮合时的传动误差。

至此，弧齿锥齿轮在单齿啮合和双齿啮合状态下，不加载与加载情况下的传动误差都可以全部确定，为高精度弧齿锥齿轮的设计提供重要依据。

三、算例

下面以一对高速重载航空用弧齿锥齿轮为例，运用上述提出的计算方法，分别计算在考虑安装误差的条件下，弧齿锥齿轮在单齿啮合下和双齿啮合下的传动误差数值大小。

表1给出了端面铣削弧齿锥齿轮的齿面设计基本参数；表2给出了弧齿锥齿轮大轮机床调整卡加工参数；表3给出了弧齿锥齿轮小轮机床调整卡加工参数。

表1弧齿锥齿轮齿面设计基本参数

表2弧齿锥齿轮大轮调整卡参数

表3弧齿锥齿轮小轮调整卡参数

图4给出了弧齿锥齿轮单齿啮合状态下不加载的传动误差曲线；图5展示的是弧齿锥齿轮单齿啮合状态下加载的传动误差曲线；图6给出的是弧齿锥齿轮双齿啮合状态下加载传动误差曲线。

对比分析结果可知，加载状态下的传动误差比不加载条件下的传动误差要大；且单齿啮合条件下的传动误差比双齿啮合状态下的传动误差要大。主要原因在于：加载时，齿面受载变形，会引起附加的传动误差；双齿啮合时，由于两对齿同时接触，承担载荷，齿面上的接触力比单齿啮合时的小，导致齿面变形小，引起的传动误差小，所以双齿啮合时的传动误差小于单齿啮合时的传动误差。由此可知，本文提出的弧齿锥齿轮传动误差数值计算方法对于齿轮设计与分析有着重要的意义。