一种应用于共轴带推力桨高速直升机的配平操纵设计方法与流程
本发明属于直升机飞行力学技术领域,特别涉及一种应用于共轴带推力桨高速直升机的配平操纵设计方法。
背景技术:
共轴高速直升机存在两副旋翼(可变转速)、尾推力桨、平垂尾等多个气动面,飞行包线覆盖0到约450km/h的速度范围。在中等速度和大速度段,直升机两副旋翼后行边卸载,而通过降低旋翼转速,主要利用其前行边在高速前飞中产生竖直方向的拉力,从而延缓了旋翼桨叶上的激波和失速对直升机起飞速度的限制。由于共轴高速直升机的升力和推进力产生方式与常规构型直升机存在很大差异,需要增加使用旋翼总距差动、周期变距差动和尾推力桨总距等操纵量,以解决常规构型直升机高速段需用功率过大和共轴刚性旋翼桨毂力矩过大等问题,达到高速飞行的目的。但这在解决上述问题的同时,又造成了操纵量过多、产生操纵冗余、难以通过传统方式配平直升机的问题。
国外从上世纪60年代开始,由西科斯基公司最早对前行桨叶概念(abc)旋翼开展探索性工作,并于1973年实现了在xh-59a型号上的装机试飞,以喷气式辅助推进器的方式,使最大平飞速度达到了240节。但由于振动强、油耗高等一系列问题,导致该型号未被军方采购。在2005年以后,随着使用旋翼作为推力系统的x2型号设计试飞,共轴高速直升机再次成为研究热点。但公开材料中对飞行稳定性、操纵性的基础——平衡飞行的操纵设计方法却基本没有介绍,或仅采用了普通铰接式共轴双旋翼直升机的平衡操纵设计方法,配平速度范围不到300km/h,还不属于高速直升机的范畴。其操纵方法设计技术仍是6变量-6自由度的普通配平。
共轴高速直升机的配平操纵设计方法,涉及到多旋翼气动干扰、刚性桨叶动力学特性分析和考虑桨毂力矩、操纵系统、发动机功率等约束进行的多轮优化迭代等多项技术。首先要解决的是高计算量复杂技术的工程化应用和多项技术的综合应用次序问题。
技术实现要素:
为了解决上述技术问题至少之一,本申请提供了一种应用于共轴带推力桨高速直升机的配平操纵设计方法,包括:
建立机体自由度平衡方程组,所述自由度平衡方程组包括直升机三个方向的合力及合力矩构成的六自由度平衡方程;
在0-a的小速度范围内,以直升机模式进行配平,所述直升机模式进行配平包括采用总距、差动总距、横向变距、纵向变距、俯仰角及滚转角6个变量以及采用所述六自由度平衡方程进行配平,获得小速度段配平值;
在a-b的过渡速度范围内,以直升机模式和推力桨模式分别进行配平,所述推力桨模式进行配平包括采用总距、差动总距、横向变距、推力桨总距、俯仰角及滚转角6个变量以及采用所述六自由度平衡方程进行配平,获取过渡速度段配平值;
计算在a-b的过渡速度范围内的直升机模式和推力桨模式配平时的需用功率,形成两条操纵模式变化线,将所述两条操纵模式变化线置于同一坐标系下,选取由功率值较小对应的操纵模式变化线的线段所组成的变化线所对应的配平值作为过渡段初始配平值;
确定在a-b的速度范围内,当旋翼桨毂俯仰力矩超过第一阈值时,基于直升机配平模式得到配平值,调整推力桨推力,在功率变化最小的情况下使所述旋翼桨毂俯仰力矩不高于所述第一阈值,获得最终的过渡段配平值;
在b以上的速度范围内,按推力桨模式进行配平,获得大速度段初始配平值;
对b以上的速度范围内的任一速度值,计算拉力功率比,若所述拉力功率比小于第二阈值,则增加差动横向变距变量以及拉力功率比方程构成7变量7方程对小于所述第二阈值的拉力功率比所对应的速度段重新进行配平,获得大速度段第二配平值;
以所述小速度段配平值调控直升机在0-a的小速度范围的气动变化,以所述最终的过渡段配平值调控直升机在a-b的过渡速度范围的气动变化,以所述大速度段初始配平值与大速度段第二配平值共同调控直升机在b以上的大速度范围的气动变化,其中,a取50-70km/h范围的任一值,b取280-320km/h范围内的任一值。
根据本申请的至少一个实施方式,所述建立机体自由度平衡方程组之前包括:
获取三旋翼尾迹结构及相互诱导速度,形成诱导速度表,所述三旋翼包括尾翼以及共轴的上旋翼与下旋翼;
根据所述诱导速度表计算共轴刚性双旋翼气动力。
根据本申请的至少一个实施方式,所述根据诱导速度表计算共轴刚性双旋翼气动力包括:
使用叶素法给出上旋翼与下旋翼在无诱导速度下的气动力初始值;
采用动量法,根据两幅旋翼气动力反求每副旋翼的自诱导速度;
根据所述诱导速度表计算每副旋翼对另一幅旋翼的诱导速度;
使用叶素法,更新两幅旋翼的气动力。
根据本申请的至少一个实施方式,所述更新两幅旋翼的气动力包括:
若更新后的气动力相比于气动力初始值超出预期限制范围,则依据更新后的气动力重新计算每副旋翼的自诱导速度,更正两幅旋翼的气动力。
根据本申请的至少一个实施方式,所述第一阈值为34000n·m。
根据本申请的至少一个实施方式,所述第二阈值为0.8,所述拉力功率比方程为:
其中,tforward为前飞拉力,pforward为前飞功率,thover表示悬停拉力,phover表示悬停功率。
根据本申请的至少一个实施方式,所述获得大速度段第二配平值之后还包括:
判断旋翼桨毂俯仰力矩是否超过第一阈值,若超过第一阈值,则将使所述旋翼桨毂俯仰力矩不高于所述第一阈值作为限制方程替换所述拉力功率比方程,对大速度段中超过第一阈值速度段重新配平,获得大速度段第三配平值,以所述大速度段初始配平值、大速度段第二配平值及大速度段第三配平值共同调控直升机在b以上的大速度范围的气动变化。
根据本申请的至少一个实施方式,所述获得大速度段第二配平值之后还包括:
计算桨尖距离,并判断所述桨尖距离是否低于第三阈值,若低于第三阈值,则将使所述桨尖距离矩不低于所述第三阈值作为限制方程替换所述拉力功率比方程,对大速度段中低于第三阈值速度段重新配平,获得大速度段第四配平值,以所述大速度段初始配平值、大速度段第二配平值及大速度段第四配平值共同调控直升机在b以上的大速度范围的气动变化。
根据本申请的至少一个实施方式,所述第三阈值为0.38m。
根据本申请的至少一个实施方式,根据所述诱导速度表计算共轴刚性双旋翼气动力包括:
采用插值法获取所述诱导速度表之外的数据。
本申请应用于共轴带推力桨高速直升机的配平操纵的设计,对复杂气动干扰和旋翼动力学分析技术,在预先计算的基础上,分别提出了能反映计算精度和变化规律的简化分析技术。针对配平操纵的多轮迭代设计流程,采用6操纵量外加2个姿态角作为配平变量,从纵横向变量解耦、变量对平衡方程影响强弱分析、增加等式约束条件等角度,在每一轮配平中进行变量与方程个数相等的配平,前一轮配平为后一轮配平提供必要的参数基础,逐级递进、检查修正,进行四轮计算后完成配平。计算中,多数速度点仅迭代1~2次,最多不超过3次。为配平操纵设计方法的工程化应用提供便利,提高了设计方法的实用价值。
附图说明
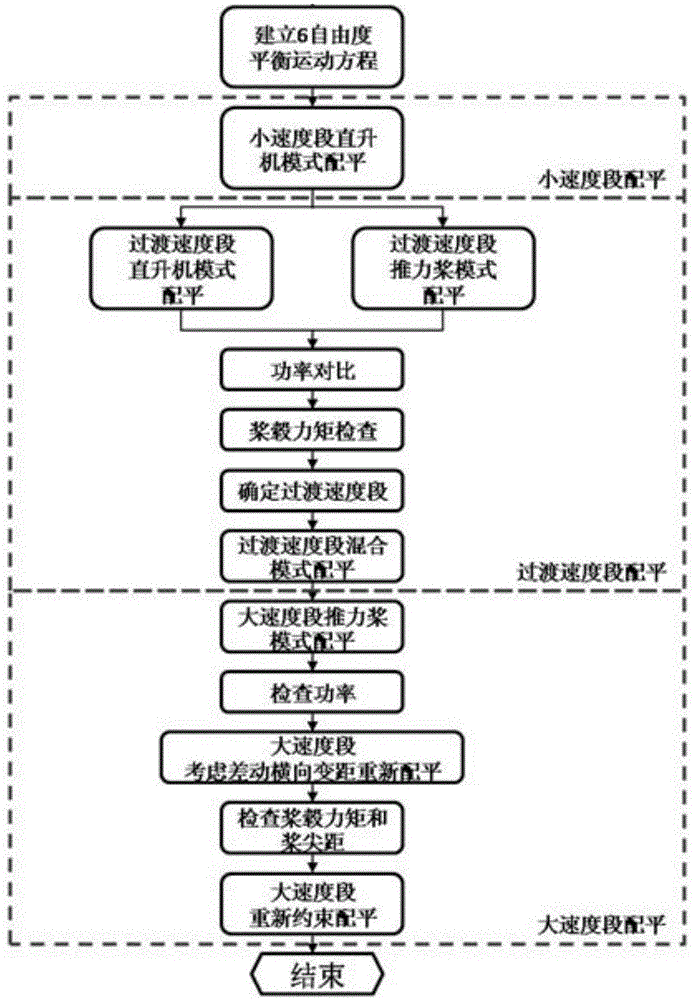
图1是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的流程图。
图2是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的悬停状态下三副旋翼收敛的自由尾迹结构图。
图3是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的大速度前飞状态下三副旋翼收敛的自由尾迹结构图。
图4是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的诱导速度场干扰示意图。
图5是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的刚性桨叶等效动力学模型示意图。
图6是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的六自由度平衡运动方程构建流程图。
图7是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的两种操纵模式功率对比示意图。
图8是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的两种操纵模式下的旋翼桨毂力矩检查示意图。
图9是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的拉力功率比随速度变化示意图。
图10是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的大速度段桨毂横向力矩变化示意图。
图11是本申请应用于共轴带推力桨高速直升机的配平操纵设计方法的一优选实施例的大速度段最小桨尖间距变化示意图。
具体实施方式
为使本申请实施的目的、技术方案和优点更加清楚,下面将结合本申请实施方式中的附图,对本申请实施方式中的技术方案进行更加详细的描述。在附图中,自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。所描述的实施方式是本申请一部分实施方式,而不是全部的实施方式。下面通过参考附图描述的实施方式是示例性的,旨在用于解释本申请,而不能理解为对本申请的限制。基于本申请中的实施方式,本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施方式,都属于本申请保护的范围。下面结合附图对本申请的实施方式进行详细说明。
在本发明的描述中,需要理解的是,术语“中心”、“纵向”、“横向”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”、“内”、“外”等指示的方位或位置关系为基于附图所示的方位或位置关系,仅是为了便于描述本发明和简化描述,而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作,因此不能理解为对本发明保护范围的限制。
本申请提供了一种应用于共轴带推力桨高速直升机的配平操纵设计方法,如图1所示,包括:
建立机体自由度平衡方程组,所述自由度平衡方程组包括直升机三个方向的合力及合力矩构成的六自由度平衡方程;
在0-a的小速度范围内,以直升机模式进行配平,所述直升机模式进行配平包括采用总距、差动总距、横向变距、纵向变距、俯仰角及滚转角6个变量以及采用所述六自由度平衡方程进行配平,获得小速度段配平值;
在a-b的过渡速度范围内,以直升机模式和推力桨模式分别进行配平,所述推力桨模式进行配平包括采用总距、差动总距、横向变距、推力桨总距、俯仰角及滚转角6个变量以及采用所述六自由度平衡方程进行配平,获取过渡速度段配平值;
计算在a-b的过渡速度范围内的直升机模式和推力桨模式配平时的需用功率,形成两条操纵模式变化线,将所述两条操纵模式变化线置于同一坐标系下,选取由功率值较小对应的操纵模式变化线的线段所组成的变化线所对应的配平值作为过渡段初始配平值;
确定在a-b的速度范围内,当旋翼桨毂俯仰力矩超过第一阈值时,基于直升机配平模式得到配平值,调整推力桨推力,在功率变化最小的情况下使所述旋翼桨毂俯仰力矩不高于所述第一阈值,获得最终的过渡段配平值;
在b以上的速度范围内,按推力桨模式进行配平,获得大速度段初始配平值;
对b以上的速度范围内的任一速度值,计算拉力功率比,若所述拉力功率比小于第二阈值,则增加差动横向变距变量以及拉力功率比方程构成7变量7方程对小于所述第二阈值的拉力功率比所对应的速度段重新进行配平,获得大速度段第二配平值;
以所述小速度段配平值调控直升机在0-a的小速度范围的气动变化,以所述最终的过渡段配平值调控直升机在a-b的过渡速度范围的气动变化,以所述大速度段初始配平值与大速度段第二配平值共同调控直升机在b以上的大速度范围的气动变化,其中,a取50-70km/h范围的任一值,b取280-320km/h范围内的任一值。
本申请提供的共轴高速直升机配平操纵设计方法,是以复杂模型分析结果修正后的全机飞行力学分析理论为基础,以过渡速度段的确定和配平操纵为中心,完成传统直升机操纵模式和高速模式下的配平操纵。配平操纵设计中考虑的约束条件是刚性旋翼桨毂力矩、上下旋翼桨叶最小间距,优化原则是三副旋翼的总需用功率尽量小、同一操纵量随速度变化的转折点尽量少。
在一些可选的实施方式中,所述建立机体自由度平衡方程组之前包括:
获取三旋翼尾迹结构及相互诱导速度,形成诱导速度表,所述三旋翼包括尾翼以及共轴的上旋翼与下旋翼;
根据所述诱导速度表计算共轴刚性双旋翼气动力。
该实施例中,图2及图3所示为在悬停和大速度前飞状态下,采用cb3d格式时间步进自由尾迹技术分析得到的共轴高速直升机三副旋翼收敛的自由尾迹结构。其中,图2所示的是悬停状态下旋翼与尾翼的轨迹,图3为大速度前飞状态下旋翼与尾翼的轨迹。
时间步进自由尾迹的cb3d格式方程可表示为:
式中,r表示尾迹涡线上每一离散节点处的位置矢量,u表示离散节点处的速度矢量,下标l、k表示离散计算中时间和空间的离散编号,δψ表示方位角,ω表示旋翼转速,γ表示人工阻尼系数。
为简化分析,将自由尾迹计算得到的三副旋翼互诱导速度场制表,在后续步骤中,用于提供给不能考虑旋翼间诱导速度的动量-叶素计算时插值使用。互诱导速度场的参数除速度值外,还包括诱导速度场圆周半径r、诱导速度场中心点坐标,典型参数的示意图如图4所示。
本实施例中,互诱导速度场包含了产生诱导速度的场半径、场中心点、场中的入流速度,场中的各方向速度分量,以50m/s前方过程中,上旋翼对下旋翼的产生的诱导速度场为例,建立的互诱导速度场如下表1-表3所示,以50m/s前方过程中,上下旋翼对推力桨产生的诱导速度场为例,建立的互诱导速度场如下表4所示,表中的θ0.7_up表示上旋翼0.7r半径处的桨叶安装角,θ0.7_down表示下旋翼0.7r径向位置处的桨叶安装角,r是旋翼半径。
表150m/s前飞,上旋翼对下旋翼诱导速度圆周外径(/r)
表250m/s前飞,上旋翼对下旋翼平面的桨毂坐标系x和y方向诱导速度中心点坐标(m)
表350m/s前飞,上旋翼对下旋翼诱导速度中均匀入流v0(m/s)
表450m/s前飞,上、下旋翼对推力桨的桨毂坐标系x和z方向平均诱导速度分量(m/s)
在一些可选实施方式中,所述根据诱导速度表计算共轴刚性双旋翼气动力包括:
使用叶素法给出上旋翼与下旋翼在无诱导速度下的气动力初始值;
采用动量法,根据两幅旋翼气动力反求每副旋翼的自诱导速度;
根据所述诱导速度表计算每副旋翼对另一幅旋翼的诱导速度;
使用叶素法,更新两幅旋翼的气动力。
例如,在上述数据被建立后,使用旋翼气动理论中常用的动量-叶素方法快速分析共轴刚性双旋翼气动力的流程如下,
(1)输入上下两副旋翼的操纵量;
(2)假设两副旋翼诱导速度均为0,使用叶素方法给出两副旋翼气动力的初始值;
(3)采用动量法,根据两副旋翼气动力反求每副旋翼的自诱导速度;
(4)根据两副旋翼诱导速度值,结合上面表1~表4中的数据,对每副旋翼的自诱导速度进行修正,并计算每副旋翼对另一副旋翼的诱导速度;
(5)根据每副旋翼处修正后的诱导速度场,使用叶素理论计算更新其气动力,并计算更新旋翼桨叶挥舞角;
(6)判断每副旋翼气动力与开始时第(2)步中计算得到的旋翼气动力偏差。如果小于预期限制范围,则进入下一步。如果高于预期限制范围,则更新第(2)步中的旋翼气动力,进入第(3)步重新计算诱导速度;
(7)向直升机全机飞行力学模型(6力素平衡方程)中输出共轴刚性双旋翼气动力。
对于共轴刚性旋翼桨叶,按一阶固有模态等效的方式,将接近刚性的桨叶以等效挥舞铰外伸量和挥舞弹簧刚度对其进行动力学建模,如图5所示,等效挥舞铰外伸量e如下式所示:
式中,w′(r)为刚性桨叶一阶振型在桨尖位置处的斜率。
等效挥舞弹簧刚度如下式所示:
mβ是桨叶质量静矩,iβ是桨叶惯性矩;k0是不旋转情况下的桨叶挥舞刚度;ωn是共轴刚性旋翼的一阶挥舞频率。
推力桨采用动量-叶素解析公式分析拉力和反扭矩,计算方程如下式所示:
式中,ct_tr是拉力系数,a∞是翼型升力线斜率,σt是实度,μt是前进比,θt是总距,mk,t是扭矩系数,cx是翼型阻力系数,κ是桨尖升力损失系数,
机身气动力采用风洞吹风数据计算。
平垂尾的升阻力计算方程如下式所示:
式中,
综合各部件气动力,直升机6自由度平衡方程如下,式中下标表示的气动部件对应关系为:旋翼(m)、机身(f)、推力桨(p)、平尾(h)、垂尾(v)。
式中,fx,fy,fz表示直升机三个向的合力,mx,my,mz表示直升机三个方向的合力矩。g表示重力加速度,
在自动倾斜器上,周期变距操纵总是施加在0°~180°和90°~
270°方位角上。通过提前操纵角γ对桨叶变距进行控制。旋翼桨叶安装角的周期变距表达式为(式中各变量含义将在随后的操纵量中注明):
θ(ψ)=θ0+a1·cos(ψ+γ)+b1·sin(ψ+γ)(7)
从操纵效果的角度,可规定共轴双旋翼的操纵量如下面多式所示,式中的下标u表示上旋翼,l表示下旋翼。
总距操纵:
纵向操纵:
横向操纵:
上述实施方式从获取旋翼参数到建立六自由度平衡运动方程如图6所示,在构建自由度平衡方程后,转入图1所示的直升机配平过程。
本实施例选取总距、总距差动、尾推力桨总距、横向周期变距、纵向周期变距、差动横向周期变距等6操纵量,外加2个姿态角(机身俯仰角和滚转角,见方程组(6)),共8个配平变量,开展配平。
使用8个配平变量,在综合考虑约束条件和优化目标的情况下实施共轴高速直升机配平操纵,具体步骤如下:
(1)小速度段直升机模式配平
在0~60km/h这一足够小的速度范围内,按照传统铰接式共轴双旋翼构型直升机的配平方法配平直升机,称为“纯直升机模式”,实施6变量-6自由度配平操纵,选用配平变量和平衡方程如表5~表6所示,具体平衡方程组如平衡方程(6)。方程的求解可以采用常用的
newton-raphson数值方法迭代求解。
表5配平变量
表6平衡方程
(2)计算过渡速度段需用功率
在60~300km/h这一足够大的速度范围内,以直升机模式方法和推力桨模式分别配平高速直升机。纯直升机模式的配平变量和方程与第(1)步相同,如表7~表8。推力桨模式中则以变化的推力桨总距替代纵向变距变量,配平变量和配平方程如表9~表10所示。
直升机模式配平变量和平衡方程如下:
表7配平变量
表8平衡方程
推力桨模式配平变量和平衡方程如下:
表9配平变量
表10平衡方程
(3)确定过渡速度段
对比两种操纵模式下的需用功率,首先取其中小者如图7所示,由于推力桨桨盘小,在直升机模式下小速度飞行更节省功率。
图7中,横坐标为速度,单位为km/h,纵坐标为需用功率,单位为kw,左侧图示的波折线段表示推力桨模式下的速度与功率关系,另一条线段表示直升机模式下的速度与功率关系,可以看出,两条线段在中间部分具有交叉,该实施例中,在交叉点之前,直升机模式下的需用功率较低,在交叉点之后,推力桨模式下的需用功率较低,选取这两段较低的线段组成右图所示的线段,由此形成的配平值作为过渡段初始配平值,也就是说,在60km/h到交叉点速度之前采用直升机模式配平,在交叉点速度到300km/h采用推力桨模式配平。
从小速度开始,首先检查更小功率的配平状态下每副旋翼的桨毂俯仰力矩(即第一阈值/最大限制值,在一些可选实施方式中,设最大限制值为34000n.m),因为共轴高速直升机采用刚性旋翼,所以在直升机配平模式下的中等速度前飞中,旋翼桨毂力矩就很容易超出最大限制值,如图8所示。俯仰力矩超标的速度范围即为过渡速度段,该图示中,横坐标为速度,纵坐标为力矩,左侧的线段为直升机模式下的速度与力矩关系,右侧的线段为推力桨模式下的速度与力矩关系。
然后,在确定的过渡速度范围内,将旋翼桨毂俯仰力矩mhub_y限制值(假设为34000n·m)作为一个方程如式(8)所示,基于直升机配平模式得到配平值、调整推力桨推力,在功率变化最小的情况下改善桨毂俯仰力矩满足要求。
mhub_y=34000n·m(8)
这样,为减小桨毂力矩进行的调整推力桨推力的配平变量和平衡方程如表11~表12所示:
表11配平变量
表12平衡方程
(4)大速度段配平
大速度段是高于过渡速度范围的所有速度点,在该速度范围内,纵向周期变距不再改变。先按如下配平变量和平衡方程选择方式,在每一速度点处作6变量-6平衡方程配平。
表13配平变量
表14平衡方程
功率超限是大速度段最大的问题,每一速度点配平结束后,即检查该速度点的拉力功率比,如果小于预期限制值(即第二阈值),如图9所示,横坐标为速度,纵坐标为拉力功率比,则在表13~14基础上,加入差动横向变距变量δb1′,拉力t和功率p比约束方程如式(9)所示,在一些可选实施方式中,第二阈值为0.8,成为7变量-7方程问题,重新配平,如表15~16。
其中forwar表示前飞、hover表示悬停。
表15配平变量
表16平衡方程
差动横向变距加入后,虽减小需用功率,但也可能会导致横向桨毂力矩过大或上下旋翼桨尖距离过小,因此需再进行一次桨毂力矩mhub_x和桨尖距离dultips检查。如果桨毂力矩过大或桨尖距过小,则需要重新配平,如图10-11所示。
图10中,可以针对桨毂横向力矩,判断旋翼桨毂俯仰力矩是否超过第一阈值,若超过第一阈值,则将使所述旋翼桨毂俯仰力矩不高于所述第一阈值作为限制方程替换所述拉力功率比方程,对大速度段中超过第一阈值速度段重新配平,获得大速度段第三配平值,以所述大速度段初始配平值、大速度段第二配平值及大速度段第三配平值共同调控直升机在b以上的大速度范围的气动变化;
图11中,可以针对桨尖距过小,计算桨尖距离,并判断所述桨尖距离是否低于第三阈值,若低于第三阈值,则将使所述桨尖距离矩不低于所述第三阈值作为限制方程替换所述拉力功率比方程,对大速度段中低于第三阈值速度段重新配平,获得大速度段第四配平值,以所述大速度段初始配平值、大速度段第二配平值及大速度段第四配平值共同调控直升机在b以上的大速度范围的气动变化。
备选实施方式中,则选取其中最难满足限制值的一者,在其超出限制范围的速度点上,以限制方程式(10)或式(11)替换拉力功率比,重新配平。以实现在尽可能减小需用功率的目标下,满足桨毂力矩和桨尖距的约束要求。
桨毂力矩限制方程:mhub_x=34000n.m(10)
上下旋翼桨尖距离限制方程:dultips=0.38m(11)
上述第三阈值即dultips=0.38m,形成表17~18的配平过程。
表17配平变量
表18平衡方程
这样,最终即在满足约束条件的情况下,得到了各速度段均匀变化的配平操纵量,且降低需用功率。
根据上述基本原理和方法,本申请可用于共轴双旋翼带推力桨构型高速直升机的配平操纵设计方法,简化的飞行力学模型,既可以反映气动干扰和桨叶挥舞运动的物理机理,又避免复杂模型工程计算的低效率。
本申请设计配平操纵策略迭代设计方法,其技术过程中各步骤物理含义明确,既有利于使用者随时分析计算结果出现的物理原因,又相比于总体设计中常用的运筹优化技术节省了大量计算科目、降低计算时间。本设计方法已经应用于某型共轴高速直升机的方案设计工作中,为发动机功率校核、共轴刚性旋翼系统设计和操纵系统设计提供了指导数据,并且可用于对未来型号试飞的科目设计和气动问题分析提供指导。
本申请能捕捉到多旋翼间精细的气动干扰现象,未因提高计算效率影响到计算精度——多数速度点处;在高速段,该配平方法捕捉到了因推力桨诱导功率急剧上升带来的全机需用功率急剧上升现象,且在200-300km/h速度范围内,该配平方法有助于降低直升机需用功率;除了在刚进入高速段时、差动横向周期变距出现了线性突增之外,各操纵量随速度变化较为平缓,这一点有利于飞行员建立良好的操纵感觉、并简化了操纵系统机构,本操纵策略设计技术适用于工程实际。
以上所述,仅为本申请的具体实施方式,但本申请的保护范围并不局限于此,任何熟悉本技术领域的技术人员在本申请揭露的技术范围内,可轻易想到的变化或替换,都应涵盖在本申请的保护范围之内。因此,本申请的保护范围应以所述权利要求的保护范围为准。
- 还没有人留言评论。精彩留言会获得点赞!