一种基于FAHP_FCA组合赋权的信息系统健康度评估方法与流程

本发明属于信息系统运维评估领域，尤其是一种基于fahp_fca组合赋权的信息系统健康度评估方法。

背景技术：

最近几年，随着信息化工作的不断发展，不少电网企业在对公司业务工作支撑力不断提升和主营业务大幅度融合的同时，也使得各信息系统的规模急剧膨胀，系统运行逐渐呈现出基础设施齐备、数据庞杂和应用广泛等特点。因此，对系统整体稳定性和运行状态的监管要求也随之提高，传统的运维检修和管理手段将无法满足复杂系统的高效管理需求。为了提升信息化运行的保障能力，准确而客观地评价信息系统的运维水平，有效地指导信息系统安全、高效、经济地运行，一种能够综合系统各性能指标和实现自动评价的信息系统健康度评估方法就显得尤为重要。

遗传算法指通过随机产生待求问题的初始解形成初始种群，每个初始解即为种群个体，再通过遗传操作来达到种群进化的目的，即通过计算种群个体适应度来进行优秀个体选择、种群个体间交叉以及种群个体本身变异等操作来产生新一代个体，通过对种群个体逐代进行遗传操作，算法终止于收敛阈值或最大进化代数。

现有技术中对分析对象各指标权重并进行综合运行质量评估方法有多种，其中申请号为cn201610268511.0、名称为“基于ahp-pca法的智能电网可持续发展综合评价方法”的发明专利公开了一种智能电网可持续发展的综合评价方法，该发明提供一种智能电网评估技术领域的基于ahp-pca算法的智能电网可持续发展综合评价方法，在评价方法投入使用的前k个月，基于层次分析法ahp对所有评价因素进行静态赋权，并根据智能电网的运行情况对各评价因素进行打分，构建ahp评价指数；评价方法运行k个月后，从第k+1个月开始基于主成分分析法pca对所有评价因素进行动态赋权，筛选出有效主成分，构建pca评价指数，pca评价指数与ahp评价指数进行结合作为智能电网可持续发展评价指数；该评价方法将层次分析法ahp与主成分分析法pca相结合，解决了智能电网评估中主观差异带来的误差问题以及主成分空有信息量而无实际含义的问题，为智能电网的可持续发展提供有效的评价方法。虽然上述方法考虑到原有ahp、pca方法各自的技术缺陷，采用ahp与pca相结合进行组合赋权的方法，克服模型评价过程中可能遇到的人为因素影响导致的主观性太强或者客观赋权太过于依赖样本数据等问题；但是，该方法使用是传统赋权算法，其只适用于指标层次结构简单、数据单一的评估场景，现有的信息系统比如企业系统，其具有数据庞大、层次结构复杂和结构之间关联紧密等特点，传统的赋权算法在整体系统运行质量评价方面无法准确地进行客观评价，导致评估方法的合理性和准确性不佳。

技术实现要素：

本发明的目的在于：本发明提供了一种基于fahp_fca组合赋权的信息系统健康度评估方法，解决现有采用ahp与pca进行组合赋权时采用的传统赋权算法只适用于结构简单、数据单一的信息系统导致评估合理性和准确性不佳的问题。

本发明采用的技术方案如下：

一种基于fahp_fca组合赋权的信息系统健康度评估方法，包括如下步骤：

步骤1：基于指标评价体系构建单个指标因素主客观组合权重的计算模型；

步骤2：通过计算模型计算各个指标因素的主客观组合权重；

步骤3：结合指标运维数据和各个指标因素的主客观组合权重计算健康度；

所述步骤1包括如下步骤：

步骤1.1：基于指标评价体系利用dematel方法综合考虑指标层次结构的横纵向影响因素对模糊层次分析过程进行加权优化，获取主观赋权的指标权重；

步骤1.2：基于指标评价体系利用因子分析法进行合理降维分析优化主成分划分过程，获取客观赋权的指标权重；

步骤1.3：根据主观赋权的指标权重和客观赋权的指标权重计算单个指标因素主客观组合权重，完成构建计算模型。

优选的，所述步骤1.1包括如下步骤：

步骤1.1.1：对指标因素进行层次化分析，构建指标评价体系；

步骤1.1.2：基于指标评价体系，采用0-1标度法构建模糊判断矩阵a：

其中，元素aij(i,j＝1,2,λ,n)表示第i个元素的重要性与第j个元素的重要性之比；

步骤1.1.3：利用方根法求模糊判断矩阵a的初始特征向量w′，计算公式如下：

步骤1.1.4：利用dematel方法，结合指标因素的影响度和被影响度计算出该指标的综合影响权重θ；

步骤1.1.5：基于指标的综合影响权重θ计算综合影响因素下的单层权向量w；

步骤1.1.6：基于单层权向量w通过遗传算法对模糊判断矩阵a进行一致性检验，获取综合因素影响下进行主观赋权的主观赋权指标权重wfahp。

优选的，所述步骤1.1.4包括如下步骤：

步骤1.1.4.1：计算指标因素之间影响度和被影响度的关系矩阵d：

d＝f^t·e

其中，d表示关系矩阵d中每个元素，f表示影响程度，e表示被影响度，t表示矩阵的转置；

步骤1.1.4.2：通过取关系矩阵d对角线元素计算关于指标因素的综合影响程度向量di：

di＝fi×ei

其中，fi表示指标因素的影响程度，ei表示指标因素的被影响程度；

步骤1.1.4.3：对综合影响程度向量di进行规范化处理获取到综合影响权重θ：

优选的，所述步骤1.1.5包括如下步骤：

步骤1.1.5.1：计算综合特征向量wi：

wi＝θw′

其中，θ表示指标的综合影响权重，w′表示模糊判断矩阵a的初始特征向量；

步骤1.1.5.2：对综合特征向量wi进行归一化：

步骤1.1.5.3：基于归一化的综合特征向量计算指标综合影响因素下的单层权向量：

优选的，所述步骤1.2包括如下步骤：

步骤1.2.1：构建基于指标评价体系的原始矩阵x：

其中，n表示结构层数，p表示每层的指标因素个数；

步骤1.2.2：对原始矩阵x进行标准化获取矩阵y：

其中，yij表示标准化后的变量值，xij表示原始矩阵x中的实际变量值，表示各变量的均值，sj表示标准差；

步骤1.2.3：分析原始矩阵x的公共因子，确定主成分个数k：

x＝ηe+ε

其中，η表示公共因子，ε表示特殊因子，e表示因子载荷矩阵；

步骤1.2.4：基于矩阵y建立协方差矩阵cx＝(cij)，计算cx的特征值，将特征值进行排序获取k个主成分元素f：

f1,f2,λfk

其中，表示变量均值，yli、ylj表示矩阵y中的元素变量；

步骤1.2.5：根据协方差矩阵cx＝(cij)构建标准化后的相关系数矩阵r＝(rij)，计算r的特征值，将特征值进行排序获取系数因子λ：

λ1≥λ2≥λ≥λp＞0；

步骤1.2.6：基于k个主成分元素f和系数因子λ计算客观赋权下的指标权重wfca：

优选的，所述步骤1.2.3包括如下步骤：

步骤1.2.3.1：对原始矩阵x公式进行变形：

x^tx＝(ηe+ε)^t(ηe+ε)；

步骤1.2.3.2：去掉特殊因子：

x^tx≈(ηe)^t(ηe)；

步骤1.2.3.3：基于步骤1.2.3.2的公式引入单位矩阵γ获取变形公式，抽取变形公式中的β作为公共因子后，对其进行因子旋转完成对指标因素分组，获取主成分个数k：

优选的，所述步骤1.3包括如下步骤：

步骤1.3.1：基于主观赋权的指标权重wfahp和客观赋权下的指标权重wfca，结合矩估计理论计算各指标主观权重的重要度系数αi和客观权重的重要度系数βi：

wfahp＝[w′1,w′2,λw′n]

wfca＝[w″1,w″2,λw″n]

步骤1.3.2：计算单个指标因素的主客观组合权重，完成构建计算模型：

综上所述，由于采用了上述技术方案，本发明的有益效果是：

1.本发明利用dematel方法考虑指标层次结构的横纵向影响因素优化模糊层次分析后进行主观赋权，利用因子分析法进行合理降维分析优化主成分划分过程，进行客观赋权，获取指标因素主客观组合权重，解决现有采用ahp与pca进行组合赋权时采用的传统赋权算法只适用于结构简单、数据单一的信息系统导致评估合理性和准确性不佳的问题，达到了提高主观评价的合理性和客观评价的准确性的效果；

2.本发明结合dematel方法优化模糊层次分析过程中指标间层级影响度的判断过程，在原本纵向赋权即分析子指标相对于父指标的影响程度的基础上综合考虑横向赋权因素即分析同级指标之间的相互被影响度，考虑影响度和被影响度，通过加权分析提高整个主观评价的合理性；

3.本发明基于因子分析法对传统pca赋权过程进行改进，通过对原始矩阵的内部结构进行分析，并结合找出的公因子对对象指标因素进行合理的分组，通过较少的主成分获取足够多的原始信息，通过分析得到的公因子对指标因素进行合理分组，避免各主成分之间由于矩阵方差贡献率的过分差异而引起评价结果过分依赖第一主成分等问题，提升了客观评价的实际准确率；

4.本发明利用遗传算法优化模糊判断矩阵的一致性检验过程，将传统复杂的一致性判断方法转化为直观的非线性问题求最优解，保证了判断矩阵的最优一致性，提高了整体系统评价的准确度与合理性，同时简化检验，避免传统一致性检验难度大的缺点；同时使用0-1标度法表示两两指标之间的重要性，避免间隔差太大导致赋权结果过于极端的缺点，利于提高整体系统评估的合理性。

附图说明

为了更清楚地说明本发明实施例的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本发明的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。

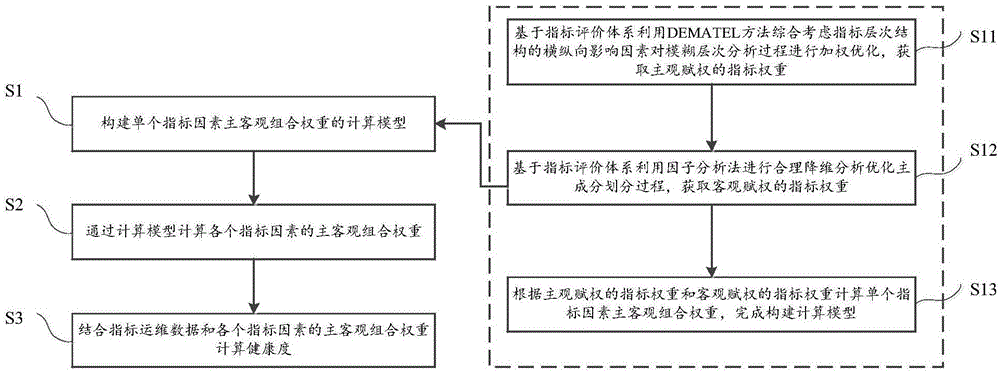
图1为本发明的方法流程图；

图2为本发明的单层指标权重计算对比效果图；

图3为本发明的一致性校验所用时间对比图；

图4为本发明的健康度客观评价误差对比图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明，即所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。通常在此处附图中描述和示出的本发明实施例的组件可以以各种不同的配置来布置和设计。

因此，以下对在附图中提供的本发明的实施例的详细描述并非旨在限制要求保护的本发明的范围，而是仅仅表示本发明的选定实施例。基于本发明的实施例，本领域技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。

需要说明的是，术语“第一”和“第二”等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。

技术问题：解决现有采用ahp与pca进行组合赋权时采用的传统赋权算法只适用于结构简单、数据单一的信息系统导致评估合理性和准确性不佳的问题；

技术手段：一种基于fahp_fca组合赋权的信息系统健康度评估方法，包括如下步骤：

步骤1：基于指标评价体系构建单个指标因素主客观组合权重的计算模型；

步骤2：通过计算模型计算各个指标因素的主客观组合权重；

步骤3：结合指标运维数据和各个指标因素的主客观组合权重计算健康度；

所述步骤1包括如下步骤：

步骤1.1：基于指标评价体系利用dematel方法综合考虑指标层次结构的横纵向影响因素对模糊层次分析过程进行加权优化，获取主观赋权的指标权重；

步骤1.2：基于指标评价体系利用因子分析法进行合理降维分析优化主成分划分过程，获取客观赋权的指标权重；

步骤1.3：根据主观赋权的指标权重和客观赋权的指标权重计算单个指标因素主客观组合权重，完成构建计算模型。

步骤1.1包括如下步骤：

步骤1.1.1：对指标因素进行层次化分析，构建指标评价体系；

步骤1.1.2：基于指标评价体系，采用0-1标度法构建模糊判断矩阵a：

其中，元素aij(i,j＝1,2,λ,n)表示第i个元素的重要性与第j个元素的重要性之比；

步骤1.1.3：利用方根法求模糊判断矩阵a的初始特征向量w′，计算公式如下：

步骤1.1.4：利用dematel方法，结合指标因素的影响度和被影响度计算出该指标的综合影响权重θ；

步骤1.1.5：基于指标的综合影响权重θ计算综合影响因素下的单层权向量w；

步骤1.1.6：基于单层权向量w通过遗传算法对模糊判断矩阵a进行一致性检验，获取综合因素影响下进行主观赋权的主观赋权指标权重wfahp。

步骤1.1.4包括如下步骤：

步骤1.1.4.1：计算指标因素之间影响度和被影响度的关系矩阵d：

d＝f^t·e

其中，d表示关系矩阵d中每个元素，f表示影响程度，e表示被影响度，t表示矩阵的转置；

步骤1.1.4.2：通过取关系矩阵d对角线元素计算关于指标因素的综合影响程度向量di：

di＝fi×ei

其中，fi表示指标因素的影响程度，ei表示指标因素的被影响程度；

步骤1.1.4.3：对综合影响程度向量di进行规范化处理获取到综合影响权重θ：

步骤1.1.5包括如下步骤：

步骤1.1.5.1：计算综合特征向量wi：

wi＝θw′

其中，θ表示指标的综合影响权重，w′表示模糊判断矩阵a的初始特征向量；

步骤1.1.5.2：对综合特征向量wi进行归一化：

步骤1.1.5.3：基于归一化的综合特征向量计算指标综合影响因素下的单层权向量：

步骤1.2包括如下步骤：

步骤1.2.1：构建基于指标评价体系的原始矩阵x：

其中，n表示结构层数，p表示每层的指标因素个数；

步骤1.2.2：对原始矩阵x进行标准化获取矩阵y：

其中，yij表示标准化后的变量值，xij表示原始矩阵x中的实际变量值，表示各变量的均值，sj表示标准差；

步骤1.2.3：分析原始矩阵x的公共因子，确定主成分个数k：

x＝ηe+ε

其中，η表示公共因子，ε表示特殊因子，e表示因子载荷矩阵；

步骤1.2.4：基于矩阵y建立协方差矩阵cx＝(cij)，计算cx的特征值，将特征值进行排序获取k个主成分元素f：

f1,f2,λfk

其中，表示变量均值，yli、ylj表示矩阵y中的元素变量；

步骤1.2.5：根据协方差矩阵cx＝(cij)构建标准化后的相关系数矩阵r＝(rij)，计算r的特征值，将特征值进行排序获取系数因子λ：

λ1≥λ2≥λ≥λp＞0；

步骤1.2.6：基于k个主成分元素f和系数因子λ计算客观赋权下的指标权重wfca：

步骤1.2.3包括如下步骤：

步骤1.2.3.1：对原始矩阵x公式进行变形：

x^tx＝(ηe+ε)^t(ηe+ε)；

步骤1.2.3.2：去掉特殊因子：

x^tx≈(ηe)^t(ηe)；

步骤1.2.3.3：基于步骤1.2.3.2的公式引入单位矩阵γ获取变形公式，抽取变形公式中的β作为公共因子后，对其进行因子旋转完成对指标因素分组，获取主成分个数k：

步骤1.3包括如下步骤：

步骤1.3.1：基于主观赋权的指标权重wfahp和客观赋权下的指标权重wfca，结合矩估计理论计算各指标主观权重的重要度系数αi和客观权重的重要度系数βi：

wfahp＝[w′1,w′2,λw′n]

wfca＝[w″1,w″2,λw″n]

步骤1.3.2：计算单个指标因素的主客观组合权重，完成构建计算模型：

技术效果：本本发明利用dematel方法考虑指标层次结构的横纵向影响因素优化模糊层次分析后进行主观赋权，利用因子分析法进行合理降维分析优化主成分划分过程，进行客观赋权，获取指标因素主客观组合权重，解决现有采用ahp与pca进行组合赋权时采用的传统赋权算法只适用于结构简单、数据单一的信息系统导致评估合理性和准确性不佳的问题，达到了提高主观评价的合理性和客观评价的准确性的效果；结合dematel方法优化模糊层次分析过程中指标间层级影响度的判断过程，在原本纵向赋权即分析子指标相对于父指标的影响程度的基础上综合考虑横向赋权因素即分析同级指标之间的相互被影响度，通过加权分析提高整个主观评价的合理性；基于因子分析法对传统pca赋权过程进行改进，通过对原始矩阵的内部结构进行分析，并结合找出的公因子对对象指标因素进行合理的分组，通过较少的主成分获取足够多的原始信息，通过分析得到的公因子对指标因素进行合理分组，避免各主成分之间由于矩阵方差贡献率的过分差异而引起评价结果过分依赖第一主成分等问题，提升了客观评价的实际准确率。

以下结合实施例对本发明的特征和性能作进一步的详细描述。

实施例1

如图1-4所示，一种基于fahp_fca组合赋权的信息系统健康度评估方法，包括如下步骤：

步骤1：构建单个指标因素主客观组合权重的计算模型；

步骤2：通过计算模型计算各个指标因素的主客观组合权重；

步骤3：结合指标运维数据和各个指标因素的主客观组合权重计算健康度；

步骤1包括如下步骤：

步骤1.1：基于指标评价体系利用dematel方法综合考虑指标层次结构的横纵向影响因素对模糊层次分析过程进行加权优化，获取主观赋权的指标权重；

步骤1.2：基于指标评价体系利用因子分析法进行合理降维分析优化主成分划分过程，获取客观赋权的指标权重；

步骤1.3：根据主观赋权的指标权重和客观赋权的指标权重计算单个指标因素主客观组合权重，完成构建计算模型。

步骤1.3.1：基于主观赋权的指标权重wfahp和客观赋权下的指标权重wfca，结合矩估计理论计算各指标主观权重的重要度系数αi和客观权重的重要度系数βi：

wfahp＝[w′1,w′2,λw′n]

wfca＝[w″1,w″2,λw″n]

步骤1.3.2：计算单个指标因素的主客观组合权重，完成构建计算模型：

本发明重点在于计算权重，计算出各个指标因素的主客观组合权重后，计算运维数据和各个指标因素的权重值之积的和获取健康度，查看健康度的值所属区间判断整个信息系统的健康状况，因步骤3为本领域的现有技术，在此不进行详细赘述；利用dematel方法考虑指标层次结构的横纵向影响因素优化模糊层次分析后进行主观赋权，利用因子分析法进行合理降维分析优化主成分划分过程，进行客观赋权，获取指标因素主客观组合权重，解决现有采用ahp与pca进行组合赋权时采用的传统赋权算法只适用于结构简单、数据单一的信息系统导致评估合理性和准确性不佳的问题，达到了提高主观评价的合理性和客观评价的准确性的效果。

实施例2

基于实施例1，步骤1.1包括如下步骤：

步骤1.1.1：对指标因素进行层次化分析，构建指标评价体系；

步骤1.1.2：基于指标评价体系，采用0-1标度法构建模糊判断矩阵a：

其中，元素aij(i,j＝1,2,λ,n)表示第i个元素的重要性与第j个元素的重要性之比；

0-1模糊标度含义：如下表所示：

步骤1.1.3：利用方根法求模糊判断矩阵a的初始特征向量w′，计算公式如下：

步骤1.1.4：利用dematel方法，结合指标因素的影响度和被影响度计算出该指标的综合影响权重θ；

步骤1.1.5：基于指标的综合影响权重θ计算综合影响因素下的单层权向量w；

步骤1.1.6：基于单层权向量w通过遗传算法对模糊判断矩阵a进行一致性检验，获取综合因素影响下进行主观赋权的主观赋权指标权重wfahp。

步骤1.1.4包括如下步骤：

步骤1.1.4.1：计算指标因素之间影响度和被影响度的关系矩阵d：

d＝f^t·e

其中，d表示关系矩阵d中每个元素，f表示影响程度，e表示被影响度，t表示矩阵的转置；

步骤1.1.4.2：通过取关系矩阵d对角线元素计算关于指标因素的综合影响程度向量di：

di＝fi×ei

其中，fi表示指标因素的影响程度，ei表示指标因素的被影响程度；

步骤1.1.4.3：对综合影响程度向量di进行规范化处理获取到综合影响权重θ：

步骤1.1.5包括如下步骤：

步骤1.1.5.1：计算综合特征向量wi：

wi＝θw′

其中，θ表示指标的综合影响权重，w′表示模糊判断矩阵a的初始特征向量；

步骤1.1.5.2：对综合特征向量wi进行归一化：

步骤1.1.5.3：基于归一化的综合特征向量计算指标综合影响因素下的单层权向量：

dematel方法：决策试行与评价实验室法，主要使用图论理论，以构造图的矩阵演算为中心，利用专家的知识和经验来解决现实世界中复杂困难问题，是一种进行因素识别与分析的有效方法。将dematel方法应用到传统的层次分析法中进行优化，主要是结合了dematel方法中因素识别与分析的思路，对层次分析过程中各对象指标的相互影响因素进行分析，一定程度上减少了专家主观评价带来的误差，从而提高各指标权重计算的准确性与客观性。

本发明结合dematel方法的思路对模糊层次分析过程中指标间层级影响度的判断过程进行优化，在原本纵向赋权(分析子指标相对于父指标的影响程度)的基础上综合考虑了横向赋权因素(分析同级指标之间的相互被影响度)，考虑影响度和被影响度进行加权优化，通过加权分析使得整个主观评价过程更具合理性。

为了与传统方法的赋权效果进行比较，选取某运维系统的实际监控数据进行测试。抽取其中的一层指标评价体系结构作为实验对象，分别采用ahp(层次分析法)、fahp(模糊层次分析法)及de-fahp(基于dematel方法优化的模糊层次分析法)计算出该层各项指标权重如下表所示：

具体效果如图2所示：传统的ahp方法由于在构建判断矩阵时采用的是1-9标度法，参数间隔较大，一定程度上扩大了基于人为主观评价产生的指标间重要性对比的误差，从而出现类似图中呈现的‘网络信息’和‘服务信息’指标权重的极端差异现象。当多层指标结构都出现类似问题时，会导致整体系统评估最终只依赖于局部权重较高的指标因素，却忽略了那些权重较低的指标因素对系统状态带来的影响。

相比于上述方法而言，fahp方法采用的是0-1标度法构建判断矩阵，通过引入模糊一致矩阵的概念，缩小了指标间重要性参数的间隔，一定程度上杜绝了极端权重分布现象对系统评估带来的影响。但是该方法往往只适用于指标层次结构较简单的评价对象，对于企业这样结构复杂、指标因素繁多的运维系统而言，采用该方法会使得最终的指标因素权重分布过于均势化，在实际系统评估时难以区分不同指标之间的影响差异，当系统运行发生故障时，无法有针对性地找到关键问题所在。

综合这两种方法的特点，本发明中对改进赋权方法过程中各指标的区分定位进行优化，突出fahp方法中的关键影响指标，优化指标赋权区分不明显的情况；现有的基于dematel方法优化后的ahp方法是基于传统的层次分析法，当应用到层次结构复杂的系统评价中时，基于指标因素分析的加权优化并不能有效缓解极端赋权差异；本发明中是对改进的fahp方法进行优化，fahp方法通过引入模糊一致矩阵的概念有效解决了ahp方法的极端赋权情况，再通过dematel方法进行因素分析，突出各指标的重要性区分定位。综上所述，本发明提出的de-fahp方法在模糊层次分析法的基础上引入指标同层次结构之间的被影响因素进行加权分析，这种结合方式不仅能有效解决ahp方法分析过程中可能遇到的极端赋权问题，而且还能通过加权分析对各指标的重要性进行突出。在应用到实际层次结构复杂的系统评价中时，能有效地减少漏评和误评等情况。

实施例3

基于实施例1或者2，步骤1.1.6：基于单层权向量w通过遗传算法对模糊判断矩阵a进行一致性检验，获取综合因素影响下进行主观赋权的主观赋权指标权重wfahp，其包括如下步骤：

1)确定目标函数和约束条件，即转化为非线性优化问题；

2)将目标的倒数作为遗传算法中的适应度函数，计算新种群个体的适应度，从中选择优秀的个体进行交叉和变异操作；

3)不断进行迭代，当前后两代适应度之差小于0.001时算法终止；否则调整模糊判断矩阵继续迭代，直到满足终止条件为止。满足一致性条件之后，即可确定综合因素影响下的主观赋权下的指标权重wfahp。

将ga-fahp(基于遗传算法优化的模糊层次分析法)与fahp(单纯的模糊层次分析法)以及ahp(传统的层次分析法)在求解一致性问题上所用的时间进行比较，抽取5组数据进行对比，单层指标项数分别为2，3，4，5，6，如图3所示：传统的层次分析法和单纯的模糊层次分析法的曲线上升幅度随着单层指标项数的增加不断变大，即随着一致性检验目标的增多，其效率下降明显；而基于遗传算法优化的模糊层次分析法整体曲线变化趋势缓慢，表明采用该算法解决一致性问题更加有效、可靠。本发明通过遗传算法对判断矩阵进行一致性检验，与传统的一致性判断方法相比，本发明将一致性检验转化为非线性优化问题求最优解，不仅简化了计算步骤，大大提高了验证效率。

实施例4

基于实施例1，所述步骤1.2包括如下步骤：

步骤1.2包括如下步骤：

步骤1.2.1：构建基于指标评价体系的原始矩阵x：

其中，n表示结构层数，p表示每层的指标因素个数；

步骤1.2.2：对原始矩阵x进行标准化获取矩阵y：

其中，yij表示标准化后的变量值，xij表示原始矩阵x中的实际变量值，表示各变量的均值，sj表示标准差；

步骤1.2.3：分析原始矩阵x的公共因子，确定主成分个数k：

x＝ηe+ε

其中，η表示公共因子，ε表示特殊因子，e表示因子载荷矩阵；

步骤1.2.4：基于矩阵y建立协方差矩阵cx＝(cij)，计算cx的特征值，将特征值进行排序获取k个主成分元素f：

f1,f2,λfk

其中，表示变量均值，yli、ylj表示矩阵y中的元素变量；

步骤1.2.5：根据协方差矩阵cx＝(cij)构建标准化后的相关系数矩阵r＝(rij)，计算r的特征值，将特征值进行排序获取系数因子λ：

λ1≥λ2≥λ≥λp＞0；

步骤1.2.6：基于k个主成分元素f和系数因子λ计算客观赋权下的指标权重wfca：

步骤1.2.3包括如下步骤：

步骤1.2.3.1：对原始矩阵x公式进行变形：

x^tx＝(ηe+ε)^t(ηe+ε)；

步骤1.2.3.2：去掉特殊因子：

x^tx≈(ηe)^t(ηe)；

步骤1.2.3.3：基于步骤1.2.3.2的公式引入单位矩阵γ获取变形公式，抽取变形公式中的β作为公共因子后，对其进行因子旋转完成对指标因素分组，获取主成分个数k：

其中，因子旋转法采用方差最大化法或者四次方最大旋转法或者等量最大法；

为了验证fca(基于因子分析过程优化的主成分分析法)相比于传统pca(主成分分析法)的优势，实验中将2种不同方法分别结合实际系统运维数据进行健康度评估测试，并对不同复杂程度的指标结构下评估值的误差进行比较，这里抽取6组数据进行对比，指标对象总数分别为10，20，30，40，50，60，测试数据如下表所示：

通过上述测试数据的对比，可得到两种方法的健康度误差分别如下：

具体效果如图4所示：随着评价系统对象的指标因素总数不断增多，整体指标评价体系结构不断复杂，传统的pca(主成分分析法)对于系统健康度评价的误差也不断增大；而基于指标体系结构分析优化的fca方法的评价误差并没有随着结构的复杂而增大，且一直保持在可控范围内。由此可见，基于因子分析过程优化的主成分分析法相比于传统的主成分分析法而言具有更准确的评估效果，也更适合对复杂运维系统进行健康诊断。主成分分析中是把主成分表示成各变量的线性组合，因子分析中则是把变量表示成各因子的线性组合。传统的主成分分析过程中，主成分个数和指标变量个数p相同，但在应用到实际问题中时，一般只选取前k(k<p)个主成分，传统的pca方法是通过计算各主成分的方差贡献率并排序，然后人为规定一个贡献率指标，取所有大于该贡献率指标的主成分的个数即为k，但该方法人为影响因素较大，本发明引入因子分析过程，通过对原始指标因素的结构分析得到公因子，并对其进行旋转操作，进而实现对指标因素的合理归类分组，确定的指标因素分组数即为主成分个数k；使用更加合理可信的方式确定个数k。本发明基于因子分析法对主成分分析的赋权过程进行改进，通过对原始矩阵的内部结构进行分析，并结合找出的公因子对对象指标因素进行合理的分组，尽量通过较少的主成分获取足够多的原始信息，同时也避免了各主成分之间由于矩阵方差贡献率的过分差异而引起的评价结果过分依赖第一主成分等问题，很大程度上提升了客观评价的实际准确率。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。