一种气动载荷与结构有限元模型双向传递方法与流程

本申请属于飞机结构强度技术领域，特别涉及一种基于多点约束的气动载荷与结构有限元模型双向传递方法。

背景技术：

对于气动与结构间载荷位移传递方法，早在1970年harder和desmarais提出了无限平板样条(ips)插值方法，该方法基于无限平板的载荷位移偏微分平衡方程和虚功原理推导得出，ips方法计算简单且可同时实现载荷与位移的传递，但其应用范围仅限于二维问题。随后appa将ips插值方法改进为薄板样条插值(tps)方法，tps方法有效实现了三维梁静气弹计算中载荷位移传递。2001年goura等人提出了一种常体积转换(cvt)方法，其基本假设为结构变形前后气动节点在结构三角形内的面积坐标保持不变，由结构节点和气动节点组成的四面体的体积在变形过程中也守恒，这样就可根据结构位移变形计算得出气动节点的位移，徐敏等通过面积因子限制提出了对该法的修正形式(icvt)，解决了变形畸形过渡时，cvt方法气动网格质量较差甚至出现负体积等问题。cvt方法只限于两种网格间的位移传递，对载荷传递并不适用，这限制了它的应用面。与此类似的还有2003年徐敏等受有限元四边形单元形函数启发提出的一种有限元四节点(fefn)插值方法，该方法计算简单，计算量小，但也仅适合于气动与结构网格间的位移插值使用。

因此，希望有一种技术方案来克服或至少减轻现有技术的至少一个上述缺陷。

技术实现要素：

本申请的目的是提供一种气动载荷与结构有限元模型双向传递方法，以解决上述问题，实现气动载荷、结构位移数据双向传递的同时，提高数据高精度传递。

本申请的技术方案是：

一种气动载荷与结构有限元模型双向传递方法，包括如下步骤：

一、构建结构模型，划分气动网格；

二、提取所述气动网格的网格点，构建气动表面点到结构单元的mpc，所述mpc指所述气动表面点与所述结构单元内的结构点的位移与力的关系函数；

三、n-s方程计算所述气动表面点的节点力；

四、利用mpc将所述节点力加载到结构有限元模型，利用nastran线性或非线性求解序列进行结构计算得到结构点位移；

五、通过mpc计算得到所述气动表面点的位移，采用弹性变形技术生成新的气动网格；

六、重复步骤三至五，直至收敛，得到所述结构模型的气动特性。

根据本申请的至少一个实施方式，所述结构模型为考虑弯曲和扭转的梁模型。

根据本申请的至少一个实施方式，所述步骤三中，利用n-s方程通过有限体积法求解梁气动表面点的节点力：

其中，ω是控制体；δω是ω的边界；ds是δω的面积矢量；w，fc，fv分别为守恒量、对流项和黏性项。

根据本申请的至少一个实施方式，所述步骤四包括，将所述气动节点力以节点力的行形式通过mpc加载到有限元模型上。

根据本申请的至少一个实施方式，所述步骤四包括：

获得结构点的变形；

根据所述变形获得所述结构点的平动位移向量t及转动位移向量r。

根据本申请的至少一个实施方式，所述获得结构点的变形包括：

根据结构点的刚度矩阵求解结构点的变形；或者

根据结构点的柔度矩阵求解结构点的变形。

根据本申请的至少一个实施方式，若对所述气动表面点影响的结构点数量为两个，则所述步骤五包括：

确定第一结构点位移引起的所述气动表面点的第一位移；

确定第二结构点位移引起的所述气动表面点的第二位移；

获取所述气动表面点到由两个结构点构成的连线的垂点；

根据所述垂点到所述两个结构点的距离分配所述第一位移及所述第二位移的权重；

根据所述第一位移与其权重以及第二位移与其权重确定所述气动表面点的最终位移。

根据本申请的至少一个实施方式，确定第一结构点位移或所述第二结构点位移引起的所述气动表面点的第一位移包括：

获取气动表面点相对于所述第一结构点或所述第二结构点的初始位置向量r；

根据公式ta＝t+r×r计算气动表面点的位移ta；

其中，t为所述第一结构点或所述第二结构点的平动位移向量，r为所述第一结构点或所述第二结构点的转动向量。

本申请至少存在以下有益技术效果：

本申请提供的气动载荷与结构有限元模型双向传递方法，相比传统的结构气动界面插值方法,具有:

1)可统一处理单梁、蒙皮、实体等不同形式的插值问题；

2)计算时间少、效率高，适合处理大型数据插值问题；

3)适合处理复杂、极度复杂外形的流/固体数据传递；

4)所加载的载荷可统一考虑压力、摩擦力等，加载精度高，无漏载等问题。

附图说明

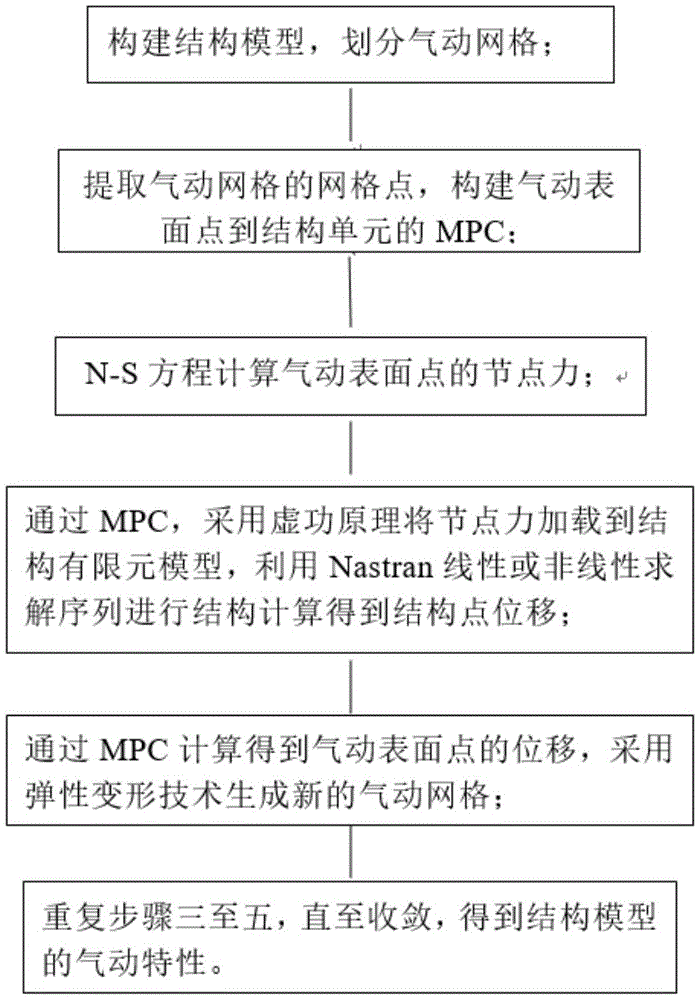
图1是本申请提供的气动载荷与结构有限元模型双向传递方法流程图；

图2是本申请中构建的结构模型；

图3是本申请梁的有限元模型；

图4是本申请中梁单元的两点约束的示意图；

图5是本申请中四边形单元的多点约束示意图。

具体实施方式

为使本申请实施的目的、技术方案和优点更加清楚，下面将结合本申请实施例中的附图，对本申请实施例中的技术方案进行更加详细的描述。在附图中，自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。所描述的实施例是本申请一部分实施例，而不是全部的实施例。下面通过参考附图描述的实施例是示例性的，旨在用于解释本申请，而不能理解为对本申请的限制。基于本申请中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本申请保护的范围。下面结合附图对本申请的实施例进行详细说明。

下面结合附图1至图5对本申请做进一步详细说明。

本申请提供的一种气动载荷与结构有限元模型双向传递方法，包括如下步骤：

一、构建结构模型，划分气动网格；

二、提取所述气动网格的网格点，构建气动表面点到结构单元的mpc，所述mpc指所述气动表面点与所述结构单元内的结构点的位移与力的关系函数；

三、n-s方程计算所述气动表面点的节点力；

四、通过mpc，采用虚功原理将所述节点力加载到结构有限元模型，利用nastran线性或非线性求解序列进行结构计算得到结构点位移；

五、通过mpc计算得到所述气动表面点的位移，采用弹性变形技术生成新的气动网格；

六、重复步骤三至五，直至收敛，得到所述气动表面点的气动特性。

在本实施例中，步骤一、如图2与图3所示，构建一种考虑弯曲和扭转的梁(或机翼)模型作为结构模型，将梁模型上的气动表面点应用nastran进行结构有限元建模，并对结构模型进行划分成气动网格；所述气动网格划分后，提取气动网格上的网格点，气动网格形成一个表面，网格点为气动网格表面上的点，简称为气动表面点。

在本实施例中，步骤二、构建的结构模型是梁模型，气动网格为梁模型上的蒙皮，即代表一种流体、气动表面，所述梁代表结构单元，构建所述气动表面点到所述梁的结构单元的mpc，构建的mpc表示所述气动表面点与所述结构单元内的结构点的位移与力的关系函数，构建的mpc能够实现流场(气动表面)与结构场(结构单元)之间双向数据传递，以便于结构变形的计算。

步骤三，在结构模型产生变形时，利用n-s方程通过有限体积法求解梁气动表面点的节点力：

其中，ω是控制体；δω是ω的边界；ds是δω的面积矢量；w，fc，fv分别为守恒量、对流项和黏性项。

步骤四、采用虚功原理将所述气动节点力以节点力的行形式通过mpc加载到有限元模型上，利用nastran线性或非线性求解序列进行结构计算得到结构点(结构单元上的一点)位移；

获得结构点的变形；

采用nastran线性求解线性静力学方程：

kx＝fg+faero

对于柔度矩阵，求解刚度矩阵的逆矩阵，采用ips插值方法得到梁表面气动网格单元的柔度矩阵c，求解静力学方程：

x＝c(fg+faero)

其中，k和x分别为刚度矩阵和结构点的变形，fg和faero分别为重力和气动表面力。

根据所述变形获得所述结构点的平动位移向量t及转动位移向量r。

步骤五、如图4所示，若对所述气动表面点影响的结构点数量为两个，则所述步骤五包括：

确定第一结构点位移n1引起的所述气动表面点的第一位移ta1；

ta1＝t1+r1×r1

确定第二结构点位移n2引起的所述气动表面点的第二位移ta2；

ta2＝t2+r2×r2

其中，气动表面点相对于第一结构点位移n1和第二结构点位移n2的初始位置向量为r1和r2，气动表面点相对于第一结构点位移n1和第二结构点位移n2的初始位置转动位移向量为r1和r2。

获取所述气动表面点到由两个结构点构成的连线的垂点p；

根据所述垂点p到所述两个结构点的距离分配所述第一位移n1及所述第二位移n2的权重；根据所述第一位移n1与其权重以及第二位移n2与其权重确定所述气动表面点的最终位移ta；如下式：

将上述得到的气动表面点的位移，采用弹性变形技术生成新的气动网格。

步骤六、重复步骤三至步骤五，直至收敛，得到变形后的气动网格，即利用mpc方法完成了气动载荷与结构有限元模型双向传递，得到所述结构模型的气动特性。

在一些可选的实施方式中，若对所述气动表面点影响的结构点数量为多个点，即为多点约束，在该实施例中，以四边形为例，搜索距离所述气动表面点最近的四边形单元，构建气动表面点到结构单元的映射关系，如图5所示，则所述步骤五为：

投影气动点(气动表面点)p到结构单元内于q点，则q点在结构单元内的二维参数坐标(ε，η)。通过以下公式中四边形等参单元的形函数可以计算出q点的四边形内的插值参数n1至n4：

假设在p点的变形过程中保持相对于结构单元的位置不变，即参数坐标不变，将插值系数作为mpc的权系数，构建气动表面点到每个结构点的mpc。通过以下公式计算出每个结构点引起的气动点变形，采用插值系数加权平均计算出单元变形引起的结构变形，如以下公式所示：

rp＝n1r1+n2r2+n3r3+n4r4

其中，r1、r2、r3以及r4分别为所述气动点p到n1至n4的初始位置向量。

以上所述，仅为本申请的具体实施方式，但本申请的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本申请揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本申请的保护范围之内。因此，本申请的保护范围应以所述权利要求的保护范围为准。