一种超静定结构的受力特性分析方法与流程

本发明涉及油气井开采技术领域，特别涉及一种超静定结构的受力特性分析方法。

背景技术：

油气井开采过程中，为提高油气采收率，增大储层接触面积，常采用直井分层和水平井分段技术。为实现这两项技术，需要采用多封隔器(即多于三个封隔器)。封隔器的作用为定位和密封，从力学角度来说，多封隔器的存在引入了多余约束的问题，即原来的油井管结构变成了超静定结构。

从上世纪60年代开始至今，有很多国内外专家学者对油气井管柱力学进行了研究。1980年，hammerlindl以双封隔器单一管柱为例，分析了管柱在四种基本效应下的轴向力及变形；1993年，冯建华等人建立了双封隔器复合管柱的轴向力计算模型，并介绍了封隔器受力及其承受压差的计算方法；2014年，吕占国分析了压裂过程中水平井多封隔器管柱的残余轴向力及强度安全性；2015年，练章华等人建立了多封隔器坐封等三种工况下的水平井压裂管柱力学计算模型，并对多级压裂管柱进行了安全性评价；2016年，张智等人建立了四种基本效应下的多封隔器复合管柱受力及变形计算模型；2017年，胡志强等人建立了双封隔器密闭环空压力预测模型，对不同工况下的封隔器管柱进行了安全校核。

现有的技术缺陷在于双封隔器结构中没有考虑超静定的约束条件，仅建立静力平衡方程进行求解，而多封隔器结构从变形协调条件建立超静定结构的变形方程，分段逐段计算管柱的受力和变形。

技术实现要素：

为了克服上述现有技术的不足，本发明的目的在于提供一种超静定结构的受力特性分析方法，具有精确计算各封隔器管柱段轴向力和轴向变形的目的，特点在于充分考虑了前一个封隔器的坐封状态对后一个封隔器的影响，可同时计算封隔器间每段管柱的轴向力，而不是像传统的计算公式分段逐段进行计算管柱的受力和变形。

为了实现上述目的，本发明采用的技术方案是：

一种超静定结构的受力特性分析方法，包括以下步骤；

步骤一：模型简化；

封隔器坐封后的四封隔器管柱简化，管柱被四个固定端固定，其中从左往右第一个固定端为封隔器1对管柱的固定约束，第二个固定端为封隔器2对管柱的固定约束，第三个固定端为封隔器3对管柱的固定约束，第四个固定端为封隔器4对管柱的固定约束；

步骤二：超静定次数的判定；

每个固定端能提供水平x方向、竖直y方向和弯矩m三个反力，由以上简化模型可知此结构为9次超静定结构，但是通常井中的管柱只承受轴向力，因此每个固定端只提供x方向的水平反力，从而此结构简化为3次超静定结构，其中三个多余约束分别为封隔器2对管柱的轴向约束、封隔器3对管柱的轴向约束以及封隔器4对管柱的轴向约束；

如果去掉超静定结构中的三个多余约束，则原结构变为静定结构，成为力法的基本结构；若去掉多余约束后在其相应位置代之以多余未知力x1、x2和x3，可以得到含有多余未知力的静定结构，此静定结构称为力法的基本体系；

步骤三：基本方程；

由于原超静定结构在任何情况下的变形量均为零，因此基本体系沿多余未知力x1、x2和x3方向的位移δ1、δ2和δ3应与原结构相同，即：

由叠加原理可得此三次超静定结构的力法基本方程为：

式中：系数δi1在数值上等于基本结构在单位力x1＝1单独作用下沿xi方向产生的位移；系数δi2在数值上等于基本结构在单位力x2＝1单独作用下沿xi方向产生的位移；系数δi3在数值上等于基本结构在单位力x3＝1单独作用下沿xi方向产生的位移；自由项δip为基本结构在外界因素(温度、压力、外载荷等)作用下沿xi方向产生的位移；i＝1，2，3；

方程(2)中各个系数及自由项的计算公式如下：

i，j＝1，2，3

式中：是基本结构由于xi＝1作用而产生的内力，n；l为管柱的长度，m；e为管柱的弹性模量，pa；a为管柱的横截面积，m²；εi为外界因素(温度、压力、外载荷等)使管柱产生的线应变；

步骤四：基本方程的求解

在基本体系中，当x1＝1单独作用时，由平衡条件可得杆1的内力为1，杆2的内力为0；当x2＝1单独作用时，由平衡条件可得杆1和杆2的内力均为1；当x3＝1单独作用时，由平衡条件可得杆1、杆2和杆3的内力均为1，则可得方程中各个系数及自由项的大小；

将各个系数及自由项的计算所得值代入基本方程(2)，则有：

超静定结构中各杆的内力可以根据叠加原理用下式计算：

解方程组(6)，可得三段管柱的轴向力分别为：

由于水平段管柱温度改变量和压力改变量处处相同，即：

δt1＝δt2＝δt3＝δt4＝δt5＝δt

δpi1＝δpi2＝δpi3＝δpi4＝δpi5＝δpi

δpo1＝δpo2＝δpo3＝δpo4＝δpo5＝δpo

因此，由温度效应和鼓胀效应引起的水平段管柱线应变也处处相等，即：

ε温1＝ε温2＝ε温3＝ε温4＝ε温5＝βδt

从而可知，由温度效应和鼓胀效应引起的水平段管柱轴向力处处相等，即：

f温1＝f温2＝f温3＝-eaβδt

本发明的有益效果：

本发明克服了传统分析方法中分段逐段求解各封隔器之间约束的局限性，可同时计算封隔器之间的每段管柱轴向力，所建立模型更符合多封隔器管柱坐封后的实际受力情况，计算结果也更精确。

附图说明

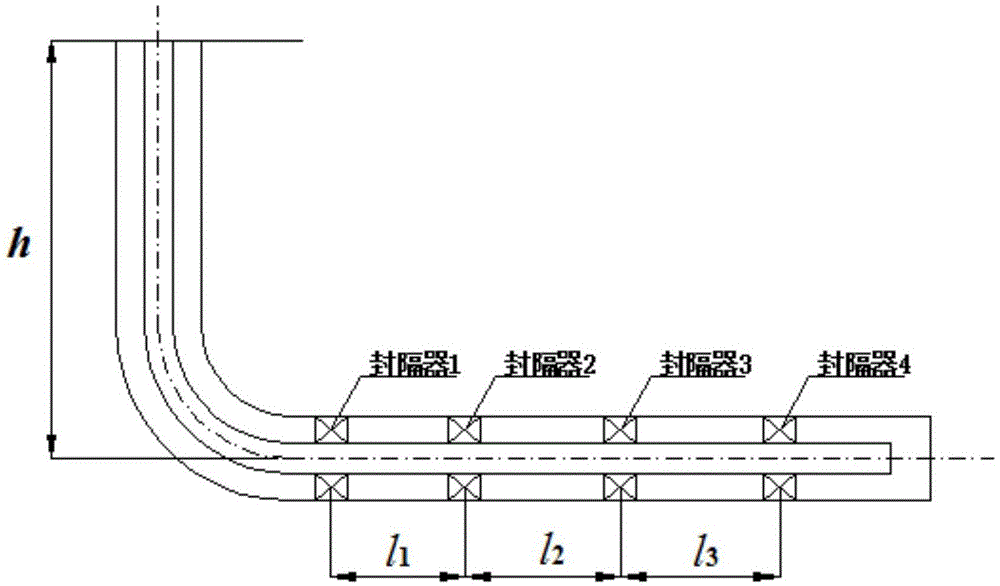
图1为水平井四封隔器管柱简图。

图2为四封隔器管柱简化模型。

图3为基本力系示意图。

具体实施方式

下面结合附图对本发明作进一步详细说明。

以水平井四封隔器单一尺寸管柱为研究对象(如图1所示)，从左往右分别为封隔器1、封隔器2、封隔器3、封隔器4；井口到水平段管柱的垂深为h；封隔器1、2之间的管柱长度为l1，为第一段管柱；封隔器2、3之间的管柱长度为l2，为第二段管柱；封隔器3、4之间的管柱长度为l3，为第三段管柱。

(1)模型简化

封隔器坐封后的四封隔器管柱简化模型如图2所示，由于本专利主要研究四个封隔器之间的三个管柱段所受轴向力的大小，所以封隔器1以前的管柱段以及封隔器4以后的管柱段不再考虑，略去。从图中可以看出，管柱被四个固定端固定，其中从左往右第一个固定端为封隔器1对管柱的固定约束，第二个固定端为封隔器2对管柱的固定约束，第三个固定端为封隔器3对管柱的固定约束，第四个固定端为封隔器4对管柱的固定约束。

(2)超静定次数的判定

因为每个固定端能提供水平x方向、竖直y方向和弯矩m三个反力，而对于图2所示结构只能列出三个平衡方程，所以由以上简化模型可知此结构为9次超静定结构。但是通常井中的管柱只承受轴向力，因此每个固定端只提供x方向的水平反力，从而此结构简化为3次超静定结构，其中三个多余约束分别为封隔器2对管柱的轴向约束、封隔器3对管柱的轴向约束以及封隔器4对管柱的轴向约束。

如果去掉超静定结构中的三个多余约束，则原结构变为静定结构，成为力法的基本结构；若去掉多余约束后在其相应位置代之以多余未知力x1、x2和x3，可以得到含有多余未知力的静定结构，此静定结构称为力法的基本体系，如图3所示。

(3)基本方程

由于原超静定结构在任何情况下的变形量均为零，因此基本体系沿多余未知力x1、x2和x3方向的位移δ1、δ2和δ3应与原结构相同，即：

由叠加原理可得此三次超静定结构的力法基本方程为：

式中：系数δi1在数值上等于基本结构在单位力x1＝1单独作用下沿xi方向产生的位移；系数δi2在数值上等于基本结构在单位力x2＝1单独作用下沿xi方向产生的位移；系数δi3在数值上等于基本结构在单位力x3＝1单独作用下沿xi方向产生的位移；自由项δip为基本结构在外界因素(温度、压力、外载荷等)作用下沿xi方向产生的位移；i＝1，2，3。

方程(2)中各个系数及自由项的计算公式如下：

i，j＝1，2，3

式中：是基本结构由于xi＝1作用而产生的内力，n；l为管柱的长度，m；e为管柱的弹性模量，pa；a为管柱的横截面积，m²；εi为外界因素(温度、压力、外载荷等)使管柱产生的线应变。

(4)基本方程的求解

由图3可知，在基本体系中，当x1＝1单独作用时，由平衡条件可得杆1的内力为1，杆2的内力为0；当x2＝1单独作用时，由平衡条件可得杆1和杆2的内力均为1；当x3＝1单独作用时，由平衡条件可得杆1、杆2和杆3的内力均为1。则可得方程中各个系数及自由项的大小如表1和表2所示。

表1系数的计算

表2自由项的计算

将表中各个系数及自由项的计算所得值代入基本方程(2)，则有：

超静定结构中各杆的内力可以根据叠加原理用下式计算：

解方程组(6)，可得三段管柱的轴向力分别为：

由于水平段管柱温度改变量和压力改变量处处相同，即：

δt1＝δt2＝δt3＝δt4＝δt5＝δt

δpi1＝δpi2＝δpi3＝δpi4＝δpi5＝δpi

δpo1＝δpo2＝δpo3＝δpo4＝δpo5＝δpo

因此，由温度效应和鼓胀效应引起的水平段管柱线应变也处处相等，即：

ε温1＝ε温2＝ε温3＝ε温4＝ε温5＝βδt

从而可知，由温度效应和鼓胀效应引起的水平段管柱轴向力处处相等，即：

f温1＝f温2＝f温3＝-eaβδt

由所推导的公式，可以定量求解多封隔器管柱这种超静定结构在不同工况下的温度效应和鼓胀效应，及在这两种效应下各个管柱段间的力学特性，进而分析管柱的强度安全性，为安全施工提供参数。

本专利运用结构力学中的力法对以超静定结构为特点的多封隔器管柱轴向力进行分析，可同时计算封隔器之间的每段管柱轴向力，更符合实际工况下多封隔器管柱的受力情况，计算结果也更精确。

本专利以直井多封隔器单一尺寸管柱为研究对象，考虑温度效应和鼓胀效应对管柱的影响，运用结构力学中的力法对以超静定结构为特点的多封隔器管柱轴向力进行分析，建立用于同时计算封隔器之间的每段管柱轴向力的计算模型，最后以四封隔器为例推导两种效应下的管柱轴向力计算公式，并和传统的计算方法进行比较，计算两者之间的差值。