一种紧凑型振动干燥/冷却流化床及其参数确定方法与流程

本发明属于振动干燥/冷却流化装置技术领域，涉及一种紧凑型振动干燥/冷却流化床及其参数确定方法。

背景技术：

在振动干燥/冷却流化领域，很多设备已经应用到工程实际中，而本专利提出一种新型紧凑型振动干燥/冷却流模型。其自动化程度高，拥有较高的干燥、冷却、流化效果，其结构紧凑，可根据需要设定若干层装置，节省空间，经济性能有所提高。本专利以五质体双机驱动动力学模型为研究对象，应用平均法和哈密顿最小作用量的原理，分别得到两激振器最终实现同步的同步性判据，分析了系统实现同步的耦合机理，定义了同步性和稳定性能力系数，数值方面，给出了系统同步能力系数曲线及稳定性系数，界定出系统处于不同共振区间下的三类相位关系：激振器间、质体间以及质体与激振器间的相位关系。而三类相位关系就是机械设备最终功能的体现。仿真方面，验证了数值结论的正确性。通过对仿真区域进行特性分析，选择适合工程实际的稳定区域，这样可根据五质体双机驱动振动同步理论为新型、高效率、高的干燥，冷却，流化效果的振动干燥/冷却设备的研制开发提供理论指导。普通的流化床有如下问题：

1.物料停留时间及干燥后的产品不均匀，导致干燥强度低。

2.单层流化床占用空间较大，且使用效率及能量利用率低，不符合国家节能减排的要求。

3.传统的多层振动流化床，质体相对较少，驱动的电机功率要求较大，且干燥流化效果相对较差，且对地面的振动影响较大。

随着振动理论的不断完善，需要依照先进的振动原理设计一款性能完善，符合要求的紧凑型振动干燥/冷却流化床，使其既提升生产率又提高能源的利用率，并且实现自动化。

技术实现要素：

针对目前干燥/冷却流化设备存在的使用大功率激振器、耗能、干燥不均匀、空间占比高等弊端，本发明提出了多质体双机驱动振动冲击破碎机的设计方法，理论上论述了该动力学模型的同步性条件及同步状态下的稳定性判据，并通过仿真分析验证数值分析的正确性，最终确定了系统的合理工作区域，以实现运动类型为线性往复运动，进而，为新型、干燥程度高、干燥冷却流化时间短的振动干燥冷却流化床的研制开发提供指导。

本发明是通过以下技术方案实现的：一种紧凑型振动干燥/冷却流化床的参数确定方法，该流化床的动力学模型如图1所示，内部四个质体构成振动系统的主振系统，主振系统中各质体分别通过四组弹簧连接在外部隔振系统质体上；

隔振系统由质体m5及固连于其上两激振器构成；每组激振器分别由偏心转子及电机组成，激振器1与激振器2反向回转，旋转半径均为r；每个偏心转子分别绕各自的旋转中心旋转，激振器1的旋转中心为o1，激振器2的旋转中心为o2，各自的旋转角度为质体m5通过弹簧k5固连于基础上，并在橡胶垫的限制下仅能沿y方向运动；

主振系统由质体m1，m2，m3，m4构成，四个质体分别通过弹簧和导向板与质体m5连接，导向板限制了质体仅能沿着弹簧方向运动，质体上方箭头方向表明质体的主运动方向；所述激振器及振动系统的参数确定方法，包括如下步骤：

步骤1,动力模型的建立

通过计算系统的动能、势能和能量散逸函数，并将其代入lagrange方程，选取yi,为广义坐标，得到系统的运动微分方程如下：

其中

mi＝mi(i＝1,2,3,4)，m5＝m5+m01+m02

式中，mi——质体i的质量(i＝1,2,3,4,5)；

m0i——激振器i质量(i＝1,2)；

β——主振弹簧与水平面的夹角；

ky,k2y,k3y,k4y——主振弹簧y方向上弹簧刚度；

k5y——隔振弹簧刚度；

fiy——y方向上阻尼系数(i＝1,2,3,4,5)；

r——激振器i的偏心距；

joi——激振器i的转动惯量(i＝1,2)；

——激振器i的相位角(i＝1,2)；

——激振器i的角速度(i＝1,2)；

——激振器i的角加速度(i＝1,2)；

步骤2,系统同步性分析

如图1，设两个激振器稳态时平均相位为对应的相位差为2α，即

利用传递函数法的得到系统的响应：

其中

a＝-m5m0⁴ωm0¹⁰+(12f0²m0³+4m5m0³k0+4f0f5m0³+4m0⁴k0+k5m0⁴+6f0²m5m0²)ωm0⁸-(36k0f0²m0²+12f0f5m0²k0+6m5k0²m0²+6f0²k5m0²+4k5m0³k0+12m0³k0²+12f0²m5k0m0+4f0³f5m0+f0⁴m5+4f0⁴m0)ωm0⁶+(6k5k0²m0²+4m5k0³m0+6f0²m5k0²+24k0²f0²m0+12f0f5k0²m0+12k0³m0²+12f0²k5k0m0+4f0³f5k0+f0⁴k5)ωm0⁴-(6f0²k5k0²+4f0f5k0³+4k5k0³m0+4k0⁴m0+m5k0⁴)ωm0²+k5k0⁴

b＝(4f0m5m0³+f5m0⁴+4f0m0⁴)ωm0⁹-(4f0k5m0³+12f0m5m0²k0+12f0³m0²+6f0²f5m0²+4f5m0³k0+24f0m0³k0+4f0³m5m0)ωm0⁷+(12f0k5m0²k0+36k0²f0m0²+6f5k0²m0²+12f0m5k0²m0+4f0³k5m0+4f0³m5k0+16f0³m0k0+12f0²f5k0m0+f0⁴f5)ωm0⁵-(4f0m5k0³+16k0³f0m0+4f5k0³m0+6f0²f5k0²+12f0k5k0²m0+4f0³k5k0)ωm0³+(4f0k5k0³+f5k0⁴)ωm0

c＝-(3m0²f0²+m0³k0)ωm0⁶+(9f0²k0m0+3m0²k0²+f0⁴)ωm0⁴-(6f0²k0²+3k0³m0)ωm0²+k0⁴

d＝-m0³f0ωm0⁷+(3f0³m0+6m0²k0f0)ωm0⁵-(9k0²m0f0+4f0³k0)ωm0³+4k0³f0ωm0

u＝m0⁴ωm0⁸-(6m0²f0²+4m0³k0)ωm0⁶+(12f0²k0m0+6m0²k0²+f0⁴)ωm0⁴-(6f0²k0²+4k0³m0)ωm0²+k0⁴

z＝-4m0³f0ωm0⁷+(12m0²k0f0+4f0³m0)ωm0⁵-(12k0²m0f0+4f0³k0)ωm0³+4k0³f0ωm0

式中，γiy——质体i在y方向上的滞后角(i＝1-5)；γ1y＝γ2y＝γ3y＝γ4y＝γ0

f1y＝f2y＝f3y＝f4y＝f0,f5y＝f5；k1y＝k2y＝k3y＝k4y＝k0,k5y＝k5；m1＝m2＝m3＝m4＝m0

质体1和4，主振弹簧和水平面的夹角为β；质体2和3，主振弹簧和水平面的夹角为(π-β)，质体5在水平面上的位移量为0，仅在y方向有运动。在较小的波动情况下，x方向上响应可得：

设质体1、2、3和4的质量相同，令m1＝m2＝m3＝m4＝m0，设主振弹簧在y方向的弹簧刚度相同，令k1y＝k2y＝k3y＝k4y＝k0,由此可以得到y方向固有频率

m——质量矩阵；

k——刚度矩阵。

δ(ω²)为特征方程

令δ(ω²)＝0，可以得到

通过计算可得到系统的固有频率:

当两个激振器能够同步运转时，有对(3)公式中系统响应关于时间t进行二阶求导，并带入式(1)中有关电机的平衡方程中，并在(0,2π)上对进行积分，取均值并整理后，得到两激振器的平衡方程如下：

式中，表示电机的电磁输出力矩其中

式中，设为标准激振器功能。

电机1，2的输出力矩之差(δt12)可表示为

重新整理式(10)可得

其中

表示电机1和电机2间的无量纲耦合力矩，其约束函数为

综上，可得两激振器的同步性判据

通过(14)，可以看出两个激振器的无量纲残余力矩之差的绝对值小于或等于无量纲耦合力矩的最大值。

对求和，并除以2tu，即可以得到两激振器平均无量纲负载力矩，表示为

两激振器平均无量纲负载力矩的约束函数如下

定义同步能力系数ζij(i,j＝1,2)，可得

用同步性能力系数来衡量各激振器间的同步能力，同步性能力系数越大，系统的同步能力越强，越容易达到同步。

步骤3，推导稳定性条件

对于双机驱动多质体运动系统，系统的动能为

系统的势能为

在一个周期内平均动能与平均势能分别为

p＝4k0f0²sin(2α-β)-8k0sin(β)f0²-8k0cos(β)f0²-4k0sin(2α+β)f0²-4k0cos(2α+β)f5²-4k0f5²sin(2α+β)+4k0f5²sin(2α-β)-8k0sin(β)f5²-8k0cos(β)f5²-4k0cos(2α+β)f0²-4k0cos(2α-β)f0²-2k5f5²sin(β)

q＝2k0f0f5[cos(γ1y-γ5y)+cos(γ2y-γ5y)+cos(γ3y-γ5y)+cos(γ4y-γ5y)]×[sin(2α+β)-sin(2α-β)+2cos(β)+2sin(β)+cos(2α-β)+cos(2α+β)]

在一个周期内系统的hamilton平均作用量(i)为

同步状态中的稳定相位差解2α对应的是hamilton平均作用量极小值点，也就是说，i的hesse矩阵正定，i的hesse矩阵表示为h,

f1＝2k0f0f5[cos(γ1-γ5)+cos(γ2-γ5)+cos(γ3-γ5)+cos(γ4-γ5)]×[-cos(2α+β)-cos(2α-β)+3sin(2α-β)-3sin(2α+β)+cos(2α+3β)+cos(2α-3β)+sin(2α+3β)-sin(2α-3β)]

f2＝3k5yf5²sin(2α+β)-3k5yf5²sin(2α-β)-k5yf5²sin(2α+3β)+k5yf5²sin(2α-3β)+4k0f0²sin(2α-3β)+4k0f5²sin(2α-3β)-4k0f5²cos(2α-3β)+4k0f5²cos(2α+β)-4k0f5²sin(2α+3β)+12k0f5²sin(2α+β)-4k0f0²cos(2α+3β)+4k0f0²cos(2α+β)-4k0f0²cos(2α-3β)-4k0f0²cos(2α+3β)+4k0f0²cos(2α-β)-12k0f0²sin(2α-β)-4k0f5²cos(2α+3β)+4k0f5²cos(2α-β)-12k0f5²sin(2α-β)+12k0f0²sin(2α+β)

f3＝16ωm0²m0f0sin(2α-β)-16ωm0²m0f0sin(2α+β)+3ωm0²m5f5sin(2α-β)-ωm0²m5f5sin(2α-3β)+ωm0²m5f5sin(2α+3β)-3ωm0²m5f5sin(2α+β)

为了使i的hesse矩阵正定，即h矩阵正定，应满足h>0。

将h定义为系统的同步条件下的稳定能力系数，当满足h>0时，系统稳定本发明的有益效果：

(1)本发明专利在模型上进行创新，选用多质体，其中一个质体连接隔振弹簧，从而达到隔振效果，多层流化方式，干燥冷却率更高。采用双机驱动，在模型上进行创新，更接近工程实践。

(2)本专利应用振动同步理论，采用双机驱动实现系统的同步工作。本专利提出的模型将工作区域选择在亚共振区域，在该区域内，系统在相同振幅的条件下，亚共振区域内激起的同样的振幅所需的激振力是其超远共振条件下的1/5～1/3。因而，在亚共振状态工作的振动系统所需驱动电机功率会相应降低，进而可以实现能源的节约。

(3)本专利可根据物料特点可在一定幅—频域内进行调整，以满足不同种类物料的处理。

(4)本专利的研究内容对于工程上振动干燥/冷却流化的机械设备，即新型、干燥程度高、干燥冷却流化时间短的振动干燥冷却流化设备。对其结构参数设计以及工作区域的选择具有重大指导作用。

(5)此外，在本专利的基础上进行扩展，来得到更多层的流化设备来满足工程需要。

附图说明

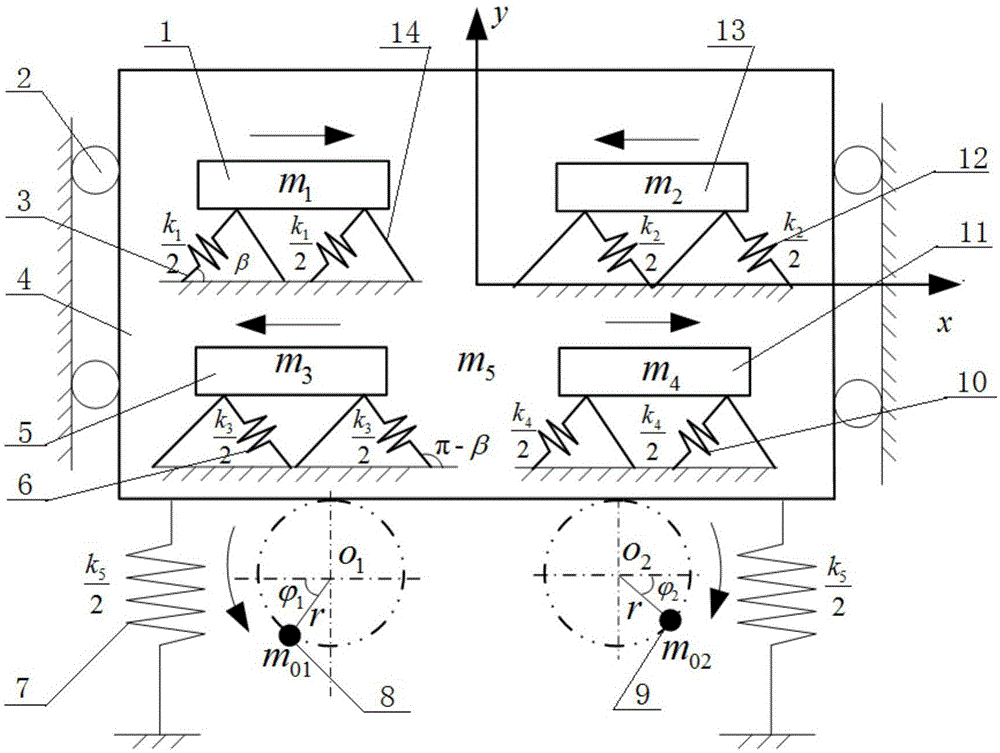
图1振动系统的动力学模型

图中：1.质体1；2.橡胶垫；3.弹簧1；4.质体5；5.质体3；6.弹簧3；

7.弹簧5；8.激振器1；9.激振器2；10.弹簧4；11.质体4；12.弹簧2；

13.质体2；14.导板。

图中各参数含义：

--激振器1相位角；

--激振器2相位角；

m01——激振器1质量；

m02——激振器2质量；

mi——质体i质量(i＝1,2,3,4,5)；

ki——弹簧i刚度(i＝1,2,3,4,5)。

图2系统之间的相位关系。

图3系统响应及其与激振器之间的相位关系。

图4同步性能力曲线。

图5稳定性能力系数。

图6相对ω0的亚共振状态(区域i)的仿真结果；

(a)激振器之间的相位差；

(b)质体在x方向的位移；

(c)质体在x方向的局部位移；

(d)质体在y方向的位移；

(e)质体在y方向的局部位移。

图7相对ω4的亚共振状态(区域ii)的仿真结果；

(a)激振器之间的相位差；

(b)质体在x方向的位移；

(c)质体在x方向的前局部位移；

(d)质体在x方向的后局部位移；

(e)质体在y方向的位移；

(f)质体在y方向的前局部位移；

(g)质体在y方向的后局部位移。

图8相对ω4的过共振状态(区域iii)的仿真结果；

(a)激振器之间的相位差；

(b)质体在x方向的位移；

(c)质体在y方向的位移。

具体实施方式

实施例1：

一种紧凑型振动干燥/冷却流化床。其动力学模型见图1，包括：1.质体1；2.橡胶垫；3.弹簧1；4.质体5；5.质体3；6.弹簧3；7.弹簧5；8.激振器1；9.激振器2；10.弹簧4；11.质体4；12.弹簧2；13.质体2；14.导板。

该模型由五个质体、两个激振器及五组弹簧组成，质体5与基座间分别装有橡胶垫，质体1,2,3,4通过弹簧将其与质体5连接，同时，通过弹簧5将质体5连接在地基上。如图1，质体5上激振器回转半径为r。激振器1与激振器2反向回转。

双质体四机驱动振动系统的数值分析

为了清晰地描述振动系统的运动特性并且验证理论结果，给出了一些数值特性分析。

在特性分析过程中，设定系统的参数：k1y＝k2y＝k3y＝k4y＝15000kn/m，k5y＝10kn/m，m5＝2000kg，m1＝m2＝m3＝m4＝1500kg，m01＝m02＝10kg，m5＝m5+m01+m02＝2020kg，因此，我们可以得到系统的固有频率为ω0＝100rad/s，ω4＝199rad/s。两台电机的型号一致(三相鼠笼式，50hz，380v，6极，0.75kw，额定转速980r/min)，给定电机参数：转子电阻rr＝3.40ω，定子电阻rs＝3.35ω,互感lm＝164mh，转子电感lr＝170mh，定子电感ls＝170mh，阻尼f1＝f2＝f3＝0.05。

(a)稳态时相位关系

对于双机驱动多质体动力学模型，在稳定状态下，激振器间的相位关系是分析系统的同步性及稳定性的重要指标。下面针对系统的相位关系进行讨论，系统在稳定状态下有三种相位关系，即激振器间的相位差关系，系统的响应以及系统的响应和激振器间的相位关系之间的相位关系。

2α表示两激振器间的相位差，当激振频率在区域1时，两激振器之间的相位差为180°，当激振频率在区域2时，激振器之间的相位差为0°，当激振频率在区域3时，激振器之间的相位差为0°和180°。

如图3所示，表示系统响应与激振器间的相位关系以及系统响应之间的相位关系。

γi(i＝1～5)表示质体i响应滞后于激振器的角度。从图示可以看出，在区域1，5个质体的滞后角均为180°；在区域2，质体1、2、3、4的相位滞后角为180°，质体5的相位滞后角为0°；在区域3，质体1、2、3、4的相位滞后角为0°，质体5的相位滞后角为180°。

(b)振动系统的同步性能力

同步性能力系数描述了两激振器间耦合力矩与系统的总平均负载力矩的一个相对比值，其值与电机本身参数无关，也可称之为广义动态对称性系数。两激振器间同步性能力系数越大，其相对耦合量就越大，两激振器就越容易实现同步，系统的同步性能力越好。

如图4系统的两个固有频率将同步性能力曲线分为3个区间，在区域i和ii，同步性能力系数随着激振频率的增加先增加后减小,在区域iii，随着激振频率的增加，同步性能力系数逐渐增加。在a点和b点处取得极小值，a点固有频率为100rad/s,b点固有频率为199rad/s。

(c)不平衡转子间的稳定状态

将系统参数代入式(25)的h中，得到系统的稳定性能力系数，如图5所示。

由稳定性能力系数曲线可以看出，随着激振频率的增加，稳定性能力系数在整个区间始终大于0，说明系统是稳定的。

实施例2,：双质体四机驱动振动系统的仿真分析

为了进一步分析和验证数值结果，通过runge-kutta方法给出了三组仿真结果。振动系统参数和电机参数在上面已给出。为了获得不同区域内系统的运动状态，一般通过改变弹簧刚度kiy(i＝1,2,3,4,5)来调整ω2和ω0的值。同时，每组将给出两个仿真结果作为比较。

(a)区域i的仿真结果

取k1y＝k2y＝k3y＝k4y＝60000kn/m，k5y＝10kn/m，z1＝0.52。系统处于第一区域，即相对于ω0的亚共振状态。

图6表示稳定状态下的电机在较短时间内，电机转速达到稳定状态，同步转速稳定在983r/min附近,60s时，给电机2加干扰，电机转速产生小的波动，很快又恢复为原来的运动状态，转速稳定在983r/min附近。

图6(b)、(c)表示质体在x方向的位移曲线。在前30s的过渡时间里，由图(b)、(c)可以看出，质体1和2的位移大小相等，运动方向相反；质体3和4的位移大小相等，运动方向相反；质体5在水平方向上处于静止状态。30s后系统处于稳定状态，由图(b)可以看出，5个质体在水平方向上的位移为0，当给电机加干扰后，系统仍能维持原来的稳定运动状态。

图6(d)、(e)表示质体在y方向的位移曲线。在前30s的过渡时间里，由图(e)y方向的局部位移曲线可以看出，5个质体的运动方向相同，质体1、2、3和4的位移量大小相等，同时要大于质体5的位移量。30s后系统处于稳定状态，由图(d)可以看出，5个质体在y方向上的位移量为0，当给电机2加干扰后，系统仍能维持原来的稳定运动状态。

(b)区域ii的仿真结果

取k1y＝k2y＝k3y＝k4y＝8000kn/m，k5y＝10kn/m，z2＝0.71。系统处于第二区域，即相对于ω4的亚共振状态。

图7表示稳定状态下的电机在较短时间内，电机转速达到稳定状态，同步转速稳定在872r/min～890r/min之间,30s时，给电机2加干扰，电机转速产生小的波动，很快又恢复为原来的运动状态。

图7(a)表示稳定状态下激振器之间的相位差关系。由图示可以得到，激振器之间的稳定相位差为0°，在30s时，给电机2加干扰，相位差曲线产生波动，之后又恢复为原来的稳定相位差。与前面所描述的特性分析中相位差关系保持一致。

图7(b)、(c)、(d)表示质体在x方向的位移曲线。由图(c)、(d)质体在x方向的局部位移曲线可以看出,质体1、2、3和4的位移量大小相等，其中，质体1和2的运动方向相反，质体3和4的运动方向相反，质体5在水平方向上的位移量为0。图(b)可以看出质体在30s加干扰处产生波动后又恢复为原来的稳定状态。

图7(e)、(f)、(g)表示质体在y方向的位移曲线。由图(f)、(g)质体在y方向的局部位移曲线可以看出,质体1、2、3和4的位移量大小相等，运动方向相同；且要小于质体5的位移量，4质体与质体5的运动方向相反，相对位移量最大。30s时加干扰，位移曲线产生波动后又恢复为原来的稳定运动状态。

(c)区域iii的仿真结果

取k1y＝k2y＝k3y＝k4y＝500kn/m，k5y＝10kn/m，z3＝2.86。系统处于第三区域，即相对于ω4的过共振状态。

图8表示稳定状态下的电机在较短时间内，电机转速达到稳定状态，同步转速稳定在983r/min附近,30s时，给电机2加干扰，电机转速发生改变，电机1的转速变小，电机2的转速变大，之后又恢复为原来的稳定运动状态。

图8(a)表示系统稳定时相位差关系。由图示可以看出相位差在达到稳定前，有5s的过渡时间，当系统达到稳定状态时，稳定相位差为180°，在30s时给电机2加干扰，相位差发生跳变，变为0°，当系统稳定后，相位差又恢复为180°。与前面所描述的特性分析中相位差关系保持一致。

图8(b)表示系统稳定时质体在x方向的位移曲线。在前30s未加干扰的情况下，质体的位移量为0，在加干扰的情况下，位移曲线发生改变，质体1和2的位移量大小相等，方向相反，质体3和4的位移量大小相等，运动方向相反。在40s时，系统恢复为稳定状态，系统的位移量为0。

图8(c)表示系统在稳定状态下，y方向的位移曲线。在前30s稳定状态下，质体的位移量为0，在30s时加干扰，位移量改变，在40s时重新恢复为稳定状态，位移量为0。

实施例3：紧凑型振动干燥/冷却流化床的示例数据参数。本发明并不仅限于此设计参数。

连接于质体1,2,3,4的弹簧，其刚度均为k1y＝k2y＝k3y＝k4y＝8000kn/m，连接于质体5上弹簧刚度k5y＝10kn/m，z2＝0.71。质体质量分别为m5＝2000kg，m1＝m2＝m3＝m4＝1500kg，激振器偏心转子质量m01＝m02＝10kg，m5＝m5+m01+m02＝2020kg，因此，我们可以得到系统的固有频率为ω0＝100rad/s，ω4＝199rad/s。两台电机的型号一致(三相鼠笼式，50hz，380v，6极，0.75kw，额定转速980r/min)，给定电机参数：转子电阻rr＝3.40ω，定子电阻rs＝3.35ω,互感lm＝164mh，转子电感lr＝170mh，定子电感ls＝170mh，阻尼f1＝f2＝f3＝0.05。此时，系统处于第二区域，即相对于ω4的亚共振状态。即满足稳定性要求，此时两质体的相对振幅满足工程的需求，其相对振幅的大小可通过改变振动系统的参数来调节。一般情况下，当不平衡转子的质量一致时，振动系统的工作效率最好。因此四组激振器质量此时选取一致。