基于时变马尔科夫过程的寿命预测方法与流程

本发明涉及可靠性领域，尤其涉及轨道交通滚动轴承的寿命预测方法。

背景技术：

安全域(safetyregion,sr)是一种从域的角度描述系统整体可安全稳定运行区域的定量模型，安全域边界与系统运行点的相对关系可提供定量化的系统不同状况下的运行安全裕度和最优控制信息。

现有技术中将安全域的概念扩展至轨道交通领域，并提出了完整的安全域估计方法框架，并针对滚动轴承进行了有益尝试。研究将轴承状态特征变量空间人为划分为两个区域，安全域与非安全域，并根据状态信息将状态特征数据直接对应至“正常”、“故障”等不同类别。然而大部分轴承性能是逐渐衰退的过程，在正常和故障之间，存在多个安全子域，且不同安全子域之间存在一定的概率转移关系。并且随着传感器技术的发展，工业工程领域对系统或关键部件运行过程的观测越来越普遍，因此产生了大量的时间序列，而且这些时间序列往往是多变量相互影响和相互联系的。因此，本发明将基于安全域估计理论的轴承退化模型扩展至多安全子域，采用时序模糊聚类算法，实现安全域与非安全域的界限、各安全子域的临界位置的自动定位。

技术实现要素：

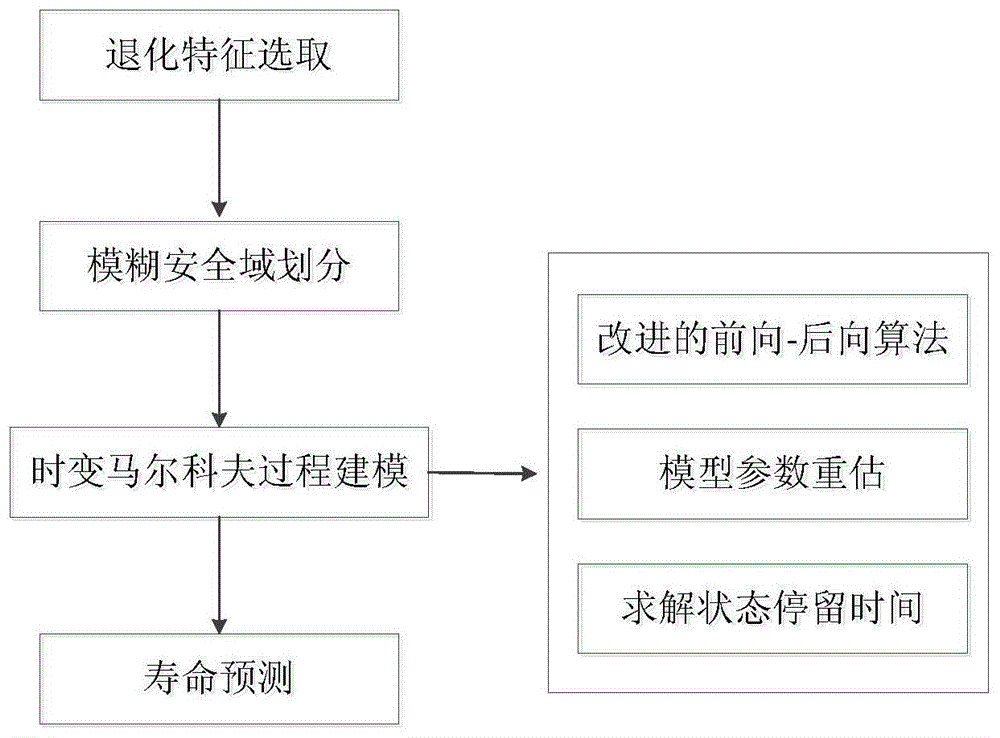
为了实现上述目的，本发明基于时变马尔科夫过程的可靠性分析及寿命预测方法主要包含四大步骤：退化特征选取，模糊安全域划分、时变马尔科夫过程建模、可靠性评估及剩余寿命预测，技术路线图如图1所示。本发明具体采用如下技术方案：

(1)提取全寿命运行特征向量，基于多元模糊分段算法进行分段，采用动态时间规整算法进行样本时间规整，完成样本数据预处理；

(2)采用模糊安全域算法对部件的状态进行划分；

(3)建立时变马尔科夫模型，利用改进的前向-后向算法计算初始前向概率，后向概率和状态序列的条件概率公式；并对模型参数进行重估；根据已确定设备当前运行状态i，得到设备在状态i逗留时间的期望，并求解设备在状态i+1,i+2,…,n的状态停留时间；计算当前状态i停留时间为的剩余寿命；

首先根据样本集，确定各状态的停留时间分布，再采用改进的向前-向后算法对模型参数进行估计：

1)当已知模型m＝(π,a,st)参数时，t时刻系统处于状态i的停留时间为t^*的概率

当t＝1时，初始前向概率为：

当t＝2,3，…,t时，前向概率递推公式为：

2)当t时刻状态i的驻留时间为时，在以后的t-t时间内产生的状态序列(st+1,st+2,...,st)的后向概率为

当t＝t时，初始后向概率公式为：

当0＜t＜t时，后向概率递推公式为：

基于前向概率公式和后向概率公式，可以得出状态向量s＝(s1,s2,...,st)，s1,s2,...,st∈{i,1≤i≤n}的条件概率公式为

3)参数估计

基于前向-后向概率公式，得到时变半马尔科夫过程模型中的参数重估计公式

ζt(i,j,st)为给定模型m和状态序列为s＝(s1,s2,...,st)，s1,s2,...,st∈{i,1≤i≤n}时，系统在状态i停留时间为st后转移到状态j的概率。

γt(i,st)为给定模型m和状态序列s，系统在时刻t在状态i停留时间为st的概率，

设ηt(i,st)为t时刻系统在状态i停留时间为st时的概率，

由可知，

表示当系统在状态i停留时间为st时，从状态i转移到状态j的期望次数，同时表示系统在当系统在状态i停留时间为st时，从状态i转移出的期望次数，因此aij(st)的重估公式为

模型m中在状态i的停留时间概率服从均值为μi，方差为的高斯分布，

4)可靠度的确定与更新

设备的故障率函数为λ(t)，寿命分布函数为f(t)，其密度函数为f(t)，f(t)＝f′(t)，可靠度函数为r(t)，则存在f(t)+r(t)＝1，λ(t)＝f(t)/r(t)。

当样本总数为m时，m(t)表示t时刻前发生故障的样本数，δm(t)表示在时间区间(t,t+δt)间发生故障的样本数，则有，

对有r(t)>0，因此，λ(t)可认为是(t,t+δt)区间故障条件概率的估计。

l表示设备的寿命周期，rul(t)表示在时刻t设备运行正常，从t到系统发生故障的剩余寿命期望，

已知设备在时刻t^*进入状态i，并在状态i的停留时间为st时，其剩余寿命等于在运行状态i的有效剩余停留时间和其他剩余状态停留时间之和，

其中，在运行状态i的有效剩余停留时间

为设备在时刻t^*进入状态i，并在状态i的停留时间为st时，在运行状态i的有效剩余停留时间；rulⁱ为设备在状态i的期望停留时间，rulⁱ＝μi；

设备在时刻t^*进入状态i，并在状态i的停留时间为st时的剩余寿命为：

附图说明

图1是本发明的技术路线图。

图2是轴承多特征对比图。

图3是特征数据分段效果图。

具体实施方式

(一)提取全寿命运行特征向量，基于多元模糊分段算法进行分段，采用dtw算法进行样本时间规整，完成样本数据预处理。

非广延熵tsallis熵是1988年巴西物理学家constantinotsallis提出的一种含有指数q的熵的表达式，基于由boltzmann-gibbs理论产生的非广延统计的机制，用来描述一个系统的混乱程度，对具有长程相互作用、长时记忆影响或系统在一个多重分形样的时空中演化的系统描述表现良好，在物理、化学、生物、医学、经济、地球物理等的各个领域均有广泛的应用。tsallis熵具有凹性、稳定性和单位时间熵产生率的有限性，然而，shanon熵、renyi熵等在轴承分析领域具有非常丰富应用的熵不具备该特性，反映在轴承特征提取中主要表现为对信号表现不够良好。因此，本发明将提取振动信号的tsallis熵作数据特征，其定义为：

tsallis熵是为了找出一个明确的q值(一般不等于1)来尽可能地刻画既不规则又不完全混沌或随机的现象。经多次试验，我们发现q＝2时能更好地描述轴承的变化特性。

(二)采用模糊安全域算法对部件的状态进行划分

本发明将基于安全域估计理论的轴承退化模型扩展至多安全子域，采用时序模糊聚类算法，实现安全域与非安全域的界限、各安全子域的临界位置的自动定位。

设样本序列为其中n为时间序列x的数据长度。若xi为多元样本，xi＝{xij|j＝1,2,...,m}，m为样本的维数。

x的一个分段可表示时间连续的系列样本点za,za+1,...,zb，记为s(a,b)＝{a≤i≤b}。假设样本序列x可以分为c段不重合部分，记为其中a1＝1,bc＝m,ak＝bk-1+1，即存在分段边界s1＜s2＜…sc，使得sk(sk-1+1,sk)。

时间序列分段可视为沿时间轴获取不重合片段约束的聚类，一般在连续的条件下对所取得的时间序列数据点按照其相似性进行聚类处理。

定义样本序列分段目标函数为一般将其定义为时间序列真实数据点与样本序列拟合函数(一般采用线性或多项式函数)数据点之间的距离。

即通过最小化目标函数，计算区域边界ak,bk,k＝1,2,...,c，获得最优分段位置。目前，动态规划和各类启发式算法常用来最小化目标函数。

其中，为第k个安全子域的聚类中心；

为xi到聚类中心的距离；

βk(ti)为xi从属于第k个安全子域的隶属度函数。

在实际情况中，安全子域之间存在模糊边界，不适合采用脆性隶属度函数。因此，本发明采用多元高斯隶属度函数，解决模糊边界问题。

与改进的gath-geva聚类算法相似，本发明采用从多元混合高斯函数作为聚类原型的序列拟合函数，通过最小化数据点与聚类原型中心之间的加权距离平方和获得最优区域划分。即：

μi,k表示样本数据点在第k个安全子域的隶属度，k＝1,2,...,c；m＝[1,∞)是决定所产生模糊聚类的加权指数，一般取m＝2；d²(zi,ηk)表示样本数据点和聚类原型之间的距离；ηk为第k个安全子域的聚类原型函数，此处为多元混合高斯函数。

假设样本序列服从期望为vk，协方差矩阵为fk的多元高斯分布，p(zi|η)表示样本数据点隶属于c个安全子域的概率密度函数。

其中，

p(ηk)是无条件聚类概率，

ηk为第k个安全子域的聚类原型函数,ηk＝{p(ηk),vk,fk|k＝1,2,...,c}。

根据概率论，gath-geva聚类算法的距离函数d²(zi,ηk)与zi在第k个安全子域的隶属度p(zi|ηk)呈反比，且样本数据中的时间变量ti与特征变量xi相互独立，则有：

其中，αk为聚类初始概率；

为第i个样本数据点的时间变量与聚类时间变量中心的距离；

为第i个样本数据点中特征变量与聚类特征中心的距离，为第k个安全子域在特征空间的聚类中心，r为特征变量距离范数ak的秩。

距离范数ak的计算方式有很多种，马氏距离是一个很好的选择，并且可用来调整变量之间的相关性，此处ak＝fk，其中为fk为多元高斯分布的模糊协方差矩阵，

为方便协方差矩阵fk的取反，必须消除变量之间的强相关性。主成分分析(principalcomponentanalysis，pca)可对高维数据进行一系列的运算和变换，在尽可能地保留原有变量信息的同时，消除高维数据之间相关性，实现降维。

设协方差矩阵fk有q个非零特征值(按降序排列)λk,l,l＝1,2,...,q及其对应的特征向量，

有

对样本数据的特征变量xi采用pca算法降到q维后得到其中

依据ppca(probabilisticprincipalcomponentanalysis)算法，其中rk是任一q×q正交变换矩阵，

至此，模糊安全域自动划分算法转换为最优化问题：

目标函数：

约束条件：

该问题可采用交替优化ao(alternatingoptimization)算法与picard迭代算法进行求解。

基本步骤为：

初始化：

给出样本序列x的分段数目和pca算法保留的特征向量空间维数，选择适合的停止条件ε,ε>0，初始化

循环计算：对于

计算聚类原型ηk的参数：

聚类初始概率：

聚类中心：

其中

权重更新：

方差更新：

距离范数：

样本序列时间参数的聚类原型中心及标准差参数计算：

聚类合并：

对两个相邻的安全子域so,sp，通过对比两者相似性，来确定其是否需要合并。由于前述用到了pca算法，采用krzanowski提出的基于pca相似因子进行作为合并准则之一，

其中，uo,q,up,q分别为安全子域so,sp特征向量的前q个主成分。

另外一个合并准则为安全子域so,sp特征向量聚类中心之间的距离：

由于聚类过程是在样本序列整体范围内进行的，因此采用模糊决策算法衡量各安全子域在整体中的聚类相似性，决策过程的整体相似性矩阵为h＝{ho,p|1≤o≤c,1≤p≤c},

当ho,o+1大于设定的阈值时，安全子域so,so+1进行合并，直至达到算法终止条件ε时结束。

(三)建立时变马尔科夫模型，利用改进的前向-后向算法计算初始前向概率，后向概率和状态序列的条件概率公式，并对模型参数进行重估；根据已确定设备当前运行状态i，得到设备在状态i逗留时间的期望，并求解设备在状态i+1,i+2,…,n的状态停留时间；计算当前状态i停留时间为的剩余寿命。

在部件安全域的划分，为马尔科夫过程的状态数量选取提供了科学的依据。我们认为，状态之间的转移概率不仅与系统所处的状态相关，还与系统在当前状态停留的时间相关。传统的hsmm模型虽然对hmm模型的markov链进行了改进，即状态停留时间服从一般分布，但并未考虑状态停留时间对状态转移概率的影响，因此将时变转移状态引入markov链模型，得到停留时间相关的状态转移矩阵(sojourntimebasedstatetransitionprobabilities)，实现时变马尔科夫过程的可靠性评估模型，记为m＝(π,a,st)，其中，π为初始状态概率分布π＝{πi},1≤i≤n，πi＝p[s1＝i],1≤i≤n，n为状态数；a为时变状态转移矩阵其中表示设备在时刻t在状态i的停留时间为时，系统从状态i转移到状态j的状态转移概率；stⁱ为在状态i的最大停留时间。同时，状态转移概率满足st为状态停留时间分布，假设服从高斯分布。

首先根据样本集，确定各状态的停留时间分布，再采用改进的baum-welch算法，对模型参数进行估计。

改进的向前-向后算法

(1)当已知模型m＝(π,a,st)参数时，t时刻系统处于状态i的停留时间为t^*的概率

当t＝1时，初始前向概率为：

当t＝2,3，…,t时，前向概率递推公式为：

(2)当t时刻状态i的驻留时间为时，在以后的t-t时间内产生的状态序列(st+1,st+2,...,st)的后向概率为

当t＝t时，初始后向概率公式为：

当0＜t＜t时，后向概率递推公式为：

基于前向概率公式和后向概率公式，可以得出状态向量s＝(s1,s2,...,st)，s1,s2,...,st∈{i,1≤i≤n}的条件概率公式为

(3)参数估计

基于前向-后向概率公式，可以得到时变半马尔科夫过程模型中的参数重估计公式

ζt(i,j,st)为给定模型m和状态序列为s＝(s1,s2,...,st)，s1,s2,...,st∈{i,1≤i≤n}时，系统在状态i停留时间为st后转移到状态j的概率。

设γt(i,st)为给定模型m和状态序列s，系统在时刻t在状态i停留时间为st的概率，

设ηt(i,st)为t时刻系统在状态i停留时间为st时的概率，

由可知，

表示当系统在状态i停留时间为st时，从状态i转移到状态j的期望次数，同时表示系统在当系统在状态i停留时间为st时，从状态i转移出的期望次数，因此aij(st)的重估公式为

假设模型m中在状态i的停留时间概率服从均值为μi，方差为的高斯分布，

(4)可靠度的确定与更新

设设备的故障率函数为λ(t)，寿命分布函数为f(t)，其密度函数为f(t)，f(t)＝f′(t)，可靠度函数为r(t)，则存在f(t)+r(t)＝1，λ(t)＝f(t)/r(t)。

当样本总数为m时，m(t)表示t时刻前发生故障的样本数，δm(t)表示在时间区间(t,t+δt)间发生故障的样本数，则有，

对有r(t)>0，因此，λ(t)可认为是(t,t+δt)区间故障条件概率的估计。

用l表示设备的寿命周期，rul(t)表示在时刻t设备运行正常，从t到系统发生故障的剩余寿命期望，

已知设备在时刻t^*进入状态i，并在状态i的停留时间为st时，其剩余寿命等于在运行状态i的有效剩余停留时间和其他剩余状态停留时间之和，

其中，在运行状态i的有效剩余停留时间

为设备在时刻t^*进入状态i，并在状态i的停留时间为st时，在运行状态i的有效剩余停留时间；rulⁱ为设备在状态i的期望停留时间，rulⁱ＝μi。

因此，设备在时刻t^*进入状态i，并在状态i的停留时间为st时的剩余寿命为：

实施例1

滚动轴承是轨道交通车辆中应用最为广泛的一种通用机械部件，但其故障发生率较高，据统计仅有10％～20％的滚动轴承可以达到设计寿命，其在使用过程中常常由于疲劳、磨损、拉伤、电腐蚀、断裂、胶合等各种原因造成机器性能异常，无法正常工作。因此本章以轴承为例验证本方法的科学性。

本发明采用法国femto-st研究所，as2m部门设计实现的专门用于测试和验证轴承pronostia实验平台上采集的轴承全寿命数据。pronostia由三个主要部分组成：旋转部分，加载部分(在测试轴承上施加径向力)和测量部分组成。

旋转部分包括带变速箱的异步电动机及其两个轴，其中一个靠近电动机，第二个放置在增量编码器的行驶侧。电机功率250w，通过变速箱传递旋转运动，它允许电机达到2830转的额定转速，从而可以提供额定转矩同时将副轴的速度保持在小于2000转/分钟的速度。符合和刚性联轴器用于产生用于传递旋转运动的连接由马达产生的轴支撑轴承。轴承支承轴引导轴承通过其内圈。保留这个固定在轴上，右侧有一个肩部，左侧有一个带螺纹的锁环。由一个部件制成的轴由两个枕块和它们的大齿轮保持。二夹具允许轴在两个枕块之间纵向阻挡。一个人机器接口允许操作员设置速度，选择电机的方向旋转并设置监控参数，如电机的瞬时温度以最高使用温度的百分比表示。

加载部分：该部件的组件分为独特且相同的铝板，部分隔离从仪器部分通过一层薄薄的聚合物。铝板支撑a气动千斤顶，垂直轴及其杠杆臂，力传感器，夹紧环的试验轴承，支撑测试轴承轴，两个轴承座及其大型超大轴承。该从气动千斤顶发出的力首先由杠杆臂放大，然后是间接的通过其夹紧环施加在试验球轴承的外圈上。这个装载部分构成了整个系统的核心。实际上，径向力减小了通过将其值设置为轴承的最大动载荷来确定轴承的使用寿命是4000n(见附录a.1)。该载荷由力致动器产生，该力致动器由a组成气动千斤顶，其供应压力由数字电动气动调节器提供。

轴承的运行条件由施加在轴承上的径向力，轴承的旋转速度以及轴承上的扭矩测得，采样频率为100hz；轴承的退化量由振动和温度传感器测得，振动信号由两个放置呈90度角的加速计采集，型号dytran3035b，分别放置在水平和垂直轴上采样频率为25.6khz，每10秒采样一次，每次采样时长0.1s，包含2560个样本点；温度传感器，型号铂金rtdpt100电阻温度检测器，位于靠近轴承外环的孔内，采样频率为10hz，每分钟采样600个点。

排除不包含温度数据和温度数据明显失常的样本。

(1)特征提取

由于轴承数据包含两组振动加速度和一组温度数据，对轴承振动加速度数据求熵，并将温度数据与振动加速度数据对齐。图2中，对轴承的同一全寿命信号分别提取了q＝2的tsallis熵，峭度，shannon熵和renyi熵，通过信号表现可知，shannon熵和renyi熵在全寿命信号周期内并不单调，且波动较大；峭度值的趋势性不够明显，且中间部分出现大于故障后的值，三种特征对轴承的性能退化均无法准确表达；tsallis熵不仅呈现全寿命周期内的单调特性，在轴承性能开始退化(图中samplenumber＝1500处)开始呈现下降趋势，在中均有所反应，且数值稳定性较好，因此，与峭度，shannon熵和renyi熵相比，tsallis熵不仅能够反应轴承性能退化趋势，而且其表现非常稳定，有利用后续确定失效阈值。

对轴承温度信号进行重采样至于振动特征信号相同长度，提取其中最大值，，三组信号分别归一化，将其变换为无量纲的表达式。

(2)数据分段结果

对上述归一化数据集中的特征数据进行自动分段，输入特征为[tsallis1,tsallis2,temperature],得到结果如图3所示。

因此，对bearing1_1的分段结果为[0,360]，[361,1800]，[1801,2740]，[2741,2803]，也就是轴承的退化过程可分为四个阶段，可认为磨合阶段、正常运行阶段、退化失效阶段和完全失效阶段，与实际使用相吻合，充分验证了多元模糊分段算法的有效性和科学合理性。我们将完全失效阶段视为非安全域；磨合阶段、正常运行阶段和退化失效阶段视为安全域，并将三个阶段分别记为安全子域1，安全子域2和安全子域3。

(3)安全域状态划分

训练样本对齐：不同的轴承具有不完全相同的退化轨迹，退化量不尽相同，因此在样本规整对齐时，并未根据退化量进行规整，而是依据退化量的变化趋势，也就是退化轨迹各点的斜率。

基于bearing1_1的分段位置，bearing1_2的分段位置为([1,289],[290,392],[393,844],[845,871])。

然而很多情况，并不是所有的轴承都会经历这四个退化阶段，在我们测试的样本中，存在无明显退化阶段而直接失效的轴承bearing2_4，和一直处于退化阶段直至失效的轴承bearing2_5。以bearing2_4为例，验证本算法的有效性。

bearing2_4的磨合阶段[1:402],退化失效阶段[403,740]，完全失效阶段[741,751]。因此得出结论：基于斜率的动态时间规整算法对不完全符合退化规律的样本仍具有较好的匹配性，不会由于强行对齐而对退化规律总结造成负面影响。

对不同的轴承样本分段结果如表1所示。

表1全部样本分段结果

(4)时变马尔科夫过程模型

在时变马尔科夫过程模型中，假设状态转移概率服从混合高斯分布概率密度函数，其状态停留概率分布函数服从单高斯分布概率密度函数，根据多元模糊分段算法，其状态数n＝4。训练过程最大迭代步数设为1000，算法误差收敛为1×e^-5。

根据轴承安全域评估结果，可得到各安全子域及非安全域的之间互相转换的初始矩阵及其在各个安全域度内的平均逗留时间，结果见表2和表3。

表2轴承安全域初始转换矩阵

表3轴承各安全域内平均逗留时间

利用上述滚动轴承的全寿命数据，得到了一个4状态的时变半马尔科夫过程故障率预测模型，即使机械部件处于同一运行状态，由于在该运行状态下的驻留时间不同，运行状态之间的转移概率和每个运行状态驻留时间的均值及方差也不相同。表4和5给出了当部件在安全子域1，停留时间为10时，运行状态转移概率和状态驻留时间的均值和方差。表6和7给出了当部件在安全子域2，停留时间为4时，运行状态转移概率和状态驻留时间的均值和方差。

表4

表5

表6

表7

对本次实验用的轴承而言，其有效寿命为安全子域1，2，3的寿命值，当轴承到达非安全域状态时，已经完全失效。

本发明所提算法的预测寿命较hmm有更高的准确性，符合寿命随时间逐渐下降趋势，由于算法采用了当前时刻所处的安全域水平及在该水平下的停留时间对状态转移概率矩阵进行了更新，算法精度会随着部件性能的逐渐退化而越来越精确，即预测寿命结果越到后期越准确。