基于快速混合迭代的MAP-TV高光谱亚像元定位方法与流程
本发明涉及高光谱亚像元定位技术领域,尤其涉及一种基于快速混合迭代的map-tv高光谱亚像元定位方法。
背景技术:
亚像元定位(subpixelmapping)技术最早由atkinson提出,旨在基于空间依赖性假设从低分辨率丰度图像中生成更高分辨率的分类图像。具体做法是通过将混合像元切割成更小的单元,根据像元中每个端元的丰度值,按照最大化空间相关性准则等,将具体地物类别相应的分配到这些较小的亚像元中,从而实现对地物的定位。
现有技术中亚像元定位算法是使用梯度下降方法求解最大后验概率正则化模型map-tv框架下的目标函数。但是使用梯度下降法求解最小化map-tv的效率低下,并且需要大量的时间和运算量。
技术实现要素:
本发明公开了一种基于快速混合迭代的map-tv高光谱亚像元定位方法,包括步骤:
获取高光谱影像;
对所述高光谱影像进行混合像元分解,得到不同端元组分的丰度;
求取最大后验概率正则化模型map-tv,包括步骤:
定义观测模型;
通过所述观测模型得到最大后验估计时对应的xc计算公式;
根据贝叶斯公式对所述xc计算公式进行处理,得到处理后的xc计算公式;
对所述处理后的xc计算公式进行tv正则化,得到最大后验概率正则化模型map-tv;
利用fista算法和分裂bregman算法相结合的算法计算xc,包括步骤:
将所述最大后验概率正则化模型map-tv进行二阶泰勒展开,得到二阶泰勒展开后模型公式;
利用所述二阶泰勒展开后模型公式和所述fista算法得到迭代的中间结果
其中,η为超参数,xc为地物端元类别c的亚像元定位结果,κ为参数,
通过所述分裂bregman算法求解
将
迭代结束得到xc;
使用赢者通吃的类别确定策略计算出最终亚像元定位结果。
优选地,所述观测模型为:
yc=dxc+nc,
其中,yc为地物端元类别c的丰度图像,xc为地物端元类别c的亚像元定位结果,d为下采样矩阵,nc为类别c的噪声。
优选地,所述最大后验估计时对应的xc计算公式为:
xc=argmax{pr(xc|yc)},
其中,
其中,pr(xc|yc)为通过丰度图像进行亚像元定位得到的后验概率,pr(yc|xc)为低分辨率影像中类别c的似然函数,pr(xc)为xc的先验概率,pr(yc)为固定值。
优选地,所述处理后的xc计算公式为:
xc=argmin{‖yc-dxc‖2+κu(xc)},
其中,u为正则化项。
优选地,所述最大后验概率正则化模型为:
其中,
优选地,
其中,
优选地,所述二阶泰勒展开后模型公式为:
优选地,所述利用fista算法和分裂bregman算法相结合的算法计算xc,进一步为:
输入λ0=0,
当所述二阶泰勒展开后模型公式未达到收敛时:
引入
定义收缩运算公式为:
解出:
结束迭代,
输出xc;
其中,
优选地,所述bregman散度距离为:
其中,
与现有技术相比,本发明提供的基于快速混合迭代的map-tv高光谱亚像元定位方法,达到如下有益效果:
第一,本发明利用fista算法和分裂bregman算法相结合的算法计算亚像元的定位结果,定位精度高,运算速度快,显著地提高亚像元定位所需的时间。
第二,本发明通过拆分高度非线性的复杂模型为几个易于计算的闭合解的子问题,有效的减少了非线性运算,节省了大量的时间和运算量,仅需几步迭代便能得到局部最优解。
下面通过附图和实施例,对本发明的技术方案做进一步的详细描述。
附图说明
此处所说明的附图用来提供对本申请的进一步理解,构成本申请的一部分,本申请的示意性实施例及其说明用于解释本申请,并不构成对本申请的不当限定。在附图中:
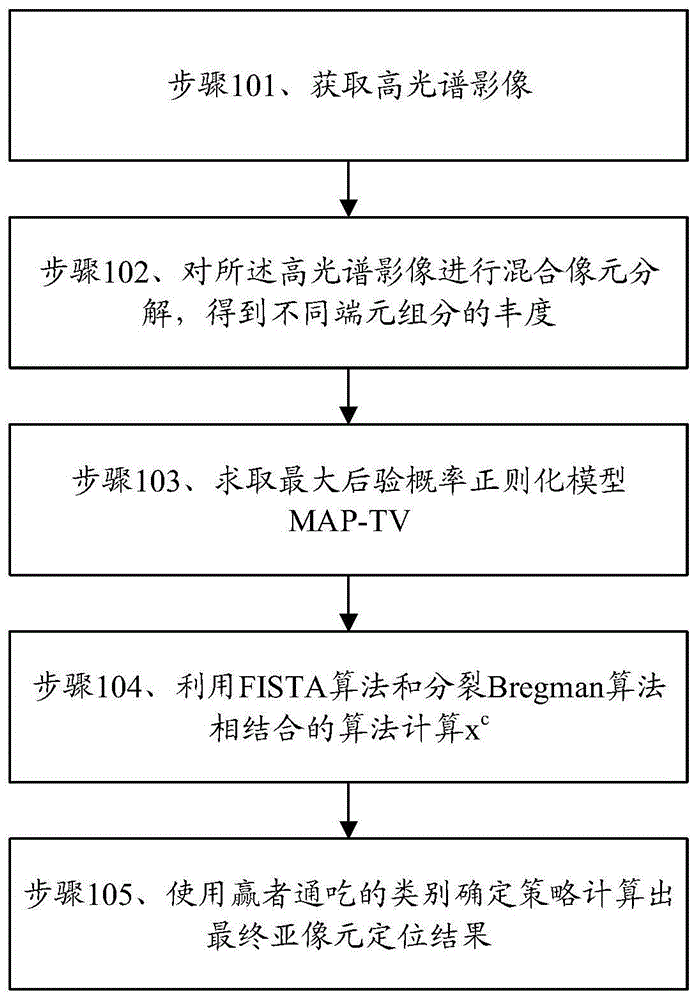
图1为本发明实施例1中基于快速混合迭代的map-tv高光谱亚像元定位方法的流程图;
图2为本发明实施例2中基于快速混合迭代的map-tv高光谱亚像元定位方法的赢者通吃的类别确定策略图。
具体实施方式
下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述。应注意到,所描述的实施例实际上仅仅是本发明一部分实施例,而不是全部的实施例,且实际上仅是说明性的,决不作为对本发明及其应用或使用的任何限制。本申请的保护范围当视所附权利要求所界定者为准。
实施例1:
参见图1所示为本申请所述基于快速混合迭代的map-tv高光谱亚像元定位方法的具体实施例,该方法包括:
步骤101、获取高光谱影像;
步骤102、对所述高光谱影像进行混合像元分解,得到不同端元组分的丰度;
步骤103、求取最大后验概率正则化模型map-tv,包括步骤:
定义观测模型;
通过所述观测模型得到最大后验估计时对应的xc计算公式(xc为亚像元定位图像中的不同位置的定位结果,即通过观测模型得到了最大后验估计时对应的像元定位结果);
根据贝叶斯公式对所述xc计算公式进行处理,得到处理后的xc计算公式;
对所述处理后的xc计算公式进行tv正则化,得到最大后验概率正则化模型map-tv;
步骤104、利用fista算法和分裂bregman算法相结合的算法计算xc,包括步骤:
将所述最大后验概率正则化模型map-tv进行二阶泰勒展开,得到二阶泰勒展开后模型公式;
利用所述二阶泰勒展开后模型公式和所述fista算法得到迭代的中间结果
其中,η为超参数,xc为地物端元类别c的亚像元定位结果,κ为参数,
通过所述分裂bregman算法求解
将
迭代结束得到xc;
步骤105、使用赢者通吃的类别确定策略计算出最终亚像元定位结果。
上述步骤103中,所述观测模型为:
yc=dxc+nc,
其中,yc为地物端元类别c的丰度图像,xc为地物端元类别c的亚像元定位结果,d为下采样矩阵,nc为类别c的噪声。
所述最大后验估计时对应的xc计算公式为:
xc=argmax{pr(xc|yc)},
其中,
其中,pr(xc|yc)为通过丰度图像进行亚像元定位得到的后验概率(即根据已知丰度图像情况下的亚像元定位结果),pr(yc|xc)为低分辨率影像中类别c的似然函数,pr(xc)为xc的先验概率,pr(yc)为固定值。
所述处理后的xc计算公式为:
xc=argmin{‖yc-dxc‖2+κu(xc)},
其中,u为正则化项。
所述最大后验概率正则化模型为:
其中,
其中,
其中,
上述步骤104中,所述二阶泰勒展开后模型公式为:
所述利用fista算法和分裂bregman算法相结合的算法计算xc,进一步为:
输入λ0=0,
当所述二阶泰勒展开后模型公式未达到收敛时:
引入
定义收缩运算公式为:
解出:
结束迭代,
输出xc;
其中,
所述bregman散度距离为:
其中,
实施例2:
本申请提供了基于快速混合迭代的map-tv高光谱亚像元定位方法的另一个实施例,该方法包括:
获取高光谱影像,对所述高光谱影像进行混合像元分解,得到不同端元组分的丰度;因为亚像元定位的目的是将低分辨率的遥感图像转换成高分辨率的图像,为达此目的,必须要获得地物组分在亚像元级别上的最优分布,因此对高光谱图像进行亚像元定位的前提是通过光谱解混得到不同端元组分在混合像元中所占的百分比;高光谱遥感影像中一个像元内包含多种物质的放射信号,每个像元的光谱信息特征是多个单一地物目标的光谱信息特征组合叠加而成的混合光谱信号,具有这种特征的像元叫做混合像元,该像元内单一地物目标的光谱叫做端元,所含端元的百分比叫做丰度。
定义观测模型,模型如下:
yc=dxc+nc(1)
其中,nc为类别c的噪声;xc为地物端元类别c的亚像元定位结果;yc为地物端元类别c的丰度图像;d为下采样矩阵,与亚像元定位图像的范围大小有关。
基于map-tv框架下的高光谱亚像元定位观测模型,是在map框架的基础上,通过引入tv正则项,来给出求解亚像元定位问题的正则化模型,继而求得最优解。假设在每个地物端元类别出现的噪声为高斯白噪声,在map框架下通过公式(1)求得最大后验估时对应的xc,具体为:
xc=argmax{pr(xc|yc)}(2)
根据贝叶斯公式:
其中,pr(xc|yc)为通过丰度图像进行亚像元定位得到的后验概率,pr(yc|xc)为低分辨率影像中类别c的似然函数,pr(xc)为xc的先验概率,pr(yc)为固定值,对公式(3)移除分母并采用对数运算,将公式(2)转化成:
xc=argmax{logpr(yc|xc)+logpr(xc)}(4)
其中似然函数可以写成:
xc=argmin{‖yc-dxc‖2+κu(xc)}(5)
其中,u为正则化项,κ为参数。如果用tv作为正则化项的话,则公式(5)即变为如下的map-tv模型:
其中,
其中,
将公式(6)改写成如下形式:
xc=argmin{f(xc)+g(xc)}(10)
其中,
通过将f(x)进行二阶泰勒展开,公式(10)可写成如下形式:
将公式(11)和公式(12)带入公式(13)中,得到如下公式:
其中,η为超参数,
使用fista(快速的迭代阈值收缩算法)后的计算过程,如下所示:
输入:λ0=0,
当不收敛时:
结束,
输出:xc。
其中,
在算法的每一次迭代过程中,通过将点
采用分裂bregman算法求解公式(17)。首先,引出对偶变量b来替换掉
上述的约束问题能够通过使用拉格朗日乘子而变成非约束问题,如下:
引入bregman散度距离,形式如下所示:
其中,
通过引入bregman散度距离,公式(20)变为:
公式(22)可以拆分成三个等价的子式。具体的计算过程如下所示:
为了求解公式(22),定义收缩运算如下:
输入:λ0=0,
当不收敛时:
结束迭代,
输出:xc。
其中,
通过拆分高度非线性的复杂模型为几个易于计算的闭合解的子问题,有效的减少了非线性运算,节省了大量的时间和运算量,仅需几步迭代便能得到局部最优解。
总体的算法如下所示:
输入:λ0,κ,η,α,
当不收敛时,
用分裂bregman算法解
结束迭代,
输出:xc。
一旦得到了所有端为结果的估计xc,使用赢者通吃wat(winner-take-all)的类别确定策略便可计算出最终的结果,如图2所示。
图2中,a、b、c代表三个类别,框中的数字为各类别亚像元在该位置的最大后验概率结果。根据赢者通吃的类别确定策略,将每个亚像元位置上的各个类别的概率值进行比较,最大值对应的类别即为该亚像元位置上的最终定位类别。如图2中左上角亚像元位置上,属于a类的概率为0.43,属于b类的概率为0.15,属于c类的概率为0.42,最大值为a类的0.43,所以左上角的亚像元最终定位的类别为a。
对比实验:
以本申请实施例1的亚像元定位方法得到的定位求解速度,与梯度下降算法得到的定位求解速度作对比,结果如表1所示。
表1亚像元定位求解速度
通过表1可以看出,本申请利用fista和分裂bregman混合算法相比用传统的梯度下降算法求解map-tv模型的似然函数有效地减少了非线性运算,节省了大量的时间和运算量。根据实验结果可知,本申请使用的方法仅需10步迭代便能得到局部最优解,相比梯度下降算法的300次迭代,迭代次数大幅降低,并且在与梯度下降拥有同样定位精度的情况下,显著地减少了亚像元定位所需要的时间。
通过以上各实施例可知,本申请存在的有益效果是:
第一,本发明利用fista算法和分裂bregman算法相结合的算法计算亚像元的定位结果,定位精度高,运算速度快,显著地提高亚像元定位所需的时间。
第二,本发明通过拆分高度非线性的复杂模型为几个易于计算的闭合解的子问题,有效的减少了非线性运算,节省了大量的时间和运算量,仅需几步迭代便能得到局部最优解。
上面通过附图和实施例,虽然已经通过例子对本发明的一些特定实施例进行了详细说明,但是本领域的技术人员应该理解,以上例子仅是为了进行说明,而不是为了限制本发明的范围。尽管参照前述实施例对本发明进行了详细的说明,对于本领域的技术人员来说,其依然可以对前述实施例所记载的技术方案进行修改,或者对其中部分技术特征进行等同替换。凡在本发明的精神和原则之内,所作的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。本发明的范围由所附权利要求来限定。
- 还没有人留言评论。精彩留言会获得点赞!