一种基于加权相似性度量的聚类集成方法与流程

本发明涉及聚类集成分析领域，特别涉及一种基于加权相似性度量的聚类集成方法。

背景技术：

聚类分析是数据挖掘中一个重要且活跃的研究领域。作为一种无监督学习方法，聚类实质上是一个密度估计问题，需要聚类的数据预先未被标注所属类别，且可以由一个混合模型产生。它的主要思想是将数据分为若干个类或簇(组)，使得簇内数据对象相似度最大化，簇间数据对象相似度最小化。近几年，大规模数据集在各个领域频繁涌现，这对聚类分析研究提出了新的挑战。面对大规模数据，传统的聚类分析算法不再像处理中小规模数据一样“得心应手”，而普遍存在处理困难、处理时间长、参数难确定、效率低下和聚类质量不高等诸多问题。聚类集成正是在这种背景下发展起来的，它寻找多个聚类解答的结合来获得更优的聚类。聚类集成在不同领域和数据集上有更好的平均性能，能发现任何单个聚类算法无法得到的解答，对于噪声，异常点，采样的变动更不敏感，还可以从聚类集体分布中估计得到簇的不确定性。聚类集成算法要解决的主要问题有两个：一个是如何产生不同的聚类从而形成一个聚类集体，第二个问题是如何从这个聚类集体中得到一个统一的聚类结果。目前国内外在聚类集成方面的研究都把重点放在第二个问题上，也就是如何从聚类集体中得到一个统一的聚类结果。

公开号为cn105844303a的专利《一种基于局部和全局信息的采样式聚类集成方法》公开了一种基于局部和全局信息的采样式聚类集成方法，首先对目标数据集进行混合采样并生成学习样本，在此学习样本空间中进行聚类分析并生成聚类划分，接下来对聚类划分进行质量评估，并根据评估结果更新目标数据集的权重向量；以上步骤进重复多轮，进而产生多个聚类划分。然后把多个聚类划分融合为一个新的特征表示，并使用传统的聚类算法对此特征表示做聚类分析，并生成集成聚类结果。该发明使得集成学习具有较强的抗噪性，同时也使其具有极高解决问题数据的能力；而且新的特征可以有效而全面地表征全局与局部的簇结构信息，使得集成学习算法在不同特点的数据集上产生好的效果。公开号为cn107169511a的专利《基于混合聚类集成选择策略的聚类集成方法》将聚类集成选择问题转化为特征选择问题，从多角度生成基础聚类结果,更具多样性，利用特征选择算法进行优化，避免人为因素及冗余度问题，考虑了局部和全局权重，有机结合各聚类结果子集，提升聚类准确性。该方法的步骤包括：输入测试数据集样本矩阵x；对数据集样本矩阵x进行聚类操作，生成基础聚类结果集合；将基础聚类结果集合转换到新特征空间，且基础聚类结果集合中的每一个聚类结果作为新特征空间的每一个特征；使用特征选择技术对特征进行聚类集成选择，得到聚类结果子集；对聚类结果子集使用赋权函数获得最终聚类结果子集；集成最终聚类结果子集，得到最终聚类结果。

由多个聚类成员的集合产生统一集成结果的过程中，一种常用的方法是利用样本在不同聚类成员中出现在同一簇内的频次进行样本间的相似性度量，构建数据集的相似性矩阵，再利用最小分割方法对数据集进行分割，从而获得统一的集成结果。然而，由于聚类集体中的各个聚类成员质量参差不齐，它们对于最终聚类集成结果的影响也不相同，忽略这些影响而单一考虑样本相似性可能导致聚类集成结果有效性降低。为此，本发明提出一种基于加权相似性度量的聚类集成方法，在利用聚类集合计算样本相似度的过程中加强质量较优的聚类成员对聚类集成结果的积极影响，同时限制质量较差成员的不利干扰，使聚类集成结果更具准确性和鲁棒性。

技术实现要素：

本发明要解决的技术问题是：设计一种聚类集成方法，依照聚类成员的质量进行加权相似性度量，在集成过程中加强高质量聚类成员的积极影响，同时抑制低质量聚类成员的不利干扰，以获得更具准确性和鲁棒性的聚类集成结果。该方法首先计算数据集中任意两个样本在每个聚类成员中对符号空间数据描述的一致性，接着计算每个聚类成员对特征空间数据描述的一致性并以此计算每个聚类成员的集成权重，在此基础上计算数据集中任意两个样本的加权相似性，然后构建数据集的加权相似性矩阵从而将聚类集成任务转换为图最小分割问题，通过利用谱聚类方法求解获得聚类集成结果，最终进行结果输出。

本发明提出的方法可用于各类数值型数据集的聚类分析任务，例如：该方法可用于识别基因表达数据中的相似模式以及拥有相同生物意义的基因集和样本集，进而在聚类分析基础上寻找相关的基因、分析基因的功能以及转录调控；该方法也可用于发现复杂网络数据集内部节点之间的结构与功能的关联特征，进行网络社区结构的划分，进而理解复杂网络的功能，探求网络中隐藏的规律并预测复杂网络的行为；该方法还可以用于处理复杂图像数据集，根据视觉特征、凸目标和背景场景等将图像划分为若干个互不重叠的区域，实现图像分割。

本发明所采用的技术方案是：一种基于加权相似性度量的聚类集成方法，对于样本数量为n的数据集在特征空间中x内的第i个样本记为xi；表示一系列在数据集x上生成的聚类成员构成的集合，其中t表示c中聚类成员的数量，表示c中第t个聚类成员，ct,k为ct中的第k个簇，st表示ct中簇的数量；将聚类划分视为对数据集的符号表示，那么聚类集合中每个聚类成员对应一个符号空间中的聚类符号向量，t个聚类符号向量构成的聚类符号向量集合记为其中表示第t个聚类成员ct的聚类符号向量，lt,k表示ct中的第k个簇的标签；表示聚类集成结果，其中c*,s表示c*中第s个簇，s*表示c*中簇的数量。本发明所述内容即利用生成聚类集成结果c*的过程，包括以下步骤：

s10、对数据集进行数据标准化处理，利用高斯核函数对特征空间中的数据集进行映射，使映射后得到的标准化数据集服从高斯分布，其中ψi表示标准化数据集中的第i个样本；

s20、计算数据集中任意两个样本在每个聚类成员中对符号空间数据描述的一致性：首先，计算聚类符号向量集合l关于数据集x的条件信息熵，用于表示利用数据集x对符号空间数据描述的不确定性；接着，计算聚类符号向量集合l关于两个样本在某一个聚类成员中所属簇的条件信息熵，用于表示利用这两个簇对符号空间数据描述的不确定性；再计算聚类符号向量集合l的以上两个条件信息熵的差值作为两个样本在这个聚类成员中对符号空间数据描述的一致性，以此类推计算任意两个样本在每个聚类成员中对符号空间数据描述的一致性；

s30、计算每个聚类成员对特征空间数据描述的一致性：首先，计算标准化数据集ψ关于数据集x的条件信息熵，用于表示利用数据集x对特征空间数据描述的不确定性；接着，计算标准化数据集ψ关于某个聚类成员的条件信息熵，用于表示该聚类成员对特征空间数据描述的不确定性；计算标准化数据集ψ的以上两个条件信息熵的差值作为该聚类成员对特征空间数据描述的一致性，以此类推计算每个聚类成员对特征空间数据描述的一致性；

s40、依据每个聚类成员对特征空间数据描述的一致性计算每个聚类成员的集成权重，分别控制各聚类成员对最终聚类集成结果的影响；

s50、利用步骤s20获得的任意两个样本在每个聚类成员中对符号空间数据描述的一致性以及步骤s40获得的每个聚类成员的集成权重计算数据集中任意两个样本间的加权相似性；

s60、将聚类集成任务转换为图最小分割问题，即使得最终的聚类集成结果中所有不在同一簇中的两个对象间的加权相似性最小；

s70、利用谱聚类方法对聚类集成任务转换得到的图最小分割问题进行求解，获得聚类集成结果c*；

s80、将聚类集成结果c*进行输出。

该方法所述步骤s10中高斯核函数如式(1)所示：

其中，参数α的取值设为||xi-xo||²的标准差，xo为数据集x中的第o个样本(i≠o)，ψo为标准化数据集ψ中的第o个样本。

该方法所述步骤s20包含：

s21、利用式(2)计算聚类符号向量集合l关于数据集x的条件信息熵，用于表示利用数据集x对符号空间数据描述的不确定性：

其中，h(lt|x)为第t个聚类成员ct的聚类符号向量lt关于数据集x的条件信息熵，可由式(3)计算：

式中，p(lt,k|x)表示聚类符号向量lt关于数据集x的条件概率，可由式(4)计算：

式中xi(lt)表示样本xi在第t个聚类符号向量上的取值，即样本xi在第t个聚类成员中对应的簇标签；

s22、对于数据集x中的任意两个样本xi和xj，它们在第t个聚类成员ct中所属的簇分别为和利用式(5)计算聚类符号向量集合l关于这两个簇的条件信息熵，用于表示利用这两个簇对符号空间数据描述的不确定性：

其中，为和构成的集合，为第t个聚类成员ct的聚类符号向量lt关于集合的条件信息熵，可由式(6)计算：

其中，表示聚类符号向量lt关于集合的条件概率，可由式(7)计算：

式中xd(lt)表示样本xd在第t个聚类符号向量上的取值，即样本xd在第t个聚类成员中对应的簇标签；

s23、计算聚类符号向量集合l关于数据集x的条件信息熵与关于的信息熵的差值作为样本xi和xj在聚类成员ct中对符号空间数据描述的一致性，如式(8)所示：

s24、利用步骤s21～s23的方法，计算数据集x中全部两个样本在每个聚类成员中对符号空间数据描述的一致性。

该方法所述步骤s30包含：

s31、利用式(9)计算标准化数据集ψ关于数据集x的条件信息熵，用于表示利用数据集x对特征空间数据描述的不确定性

其中，h(ψ|x)为标准化数据集ψ关于数据集x的条件信息熵，表示标准化数据集ψ的方差，由式(10)进行计算：

其中，μψ为标准化数据集ψ的期望，满足式(11)：

s32、计算标准化数据集ψ关于每个聚类成员的条件信息熵，用于描述各聚类成员对特征空间数据描述的一致性，其中ψ关于第t个聚类成员ct的条件信息熵可由式(12)计算：

其中，h(ψ|ct)为标准化数据集ψ关于第t个聚类成员ct的条件信息熵，表示ct中样本的方差，由式(13)进行计算：

其中，为ct中样本的期望，满足式(14)：

式中，ψe为标准化数据集ψ中的第e个样本，xe为数据集x的第e个样本，xf为数据集x的第f个样本(e≠f)，xg和xh为数据集x中不相同的任意两个样本；

s33、计算标准化数据集ψ的以上两个条件信息熵的差值，作为该聚类成员对特征空间数据描述的一致性，其中第t个聚类成员ct在ψ上的一致性度量由式(15)计算：

i(ψ|ct)＝h(ψ|x)-h(ψ|ct)(15)

其中，i(ψ|ct)表示ct在ψ上的一致性度量；

s34、利用步骤s31～s33的方法，逐个计算每个聚类成员对特征空间数据描述的一致性。

该方法所述步骤s40中依据每个聚类成员对特征空间数据描述的一致性计算每个聚类成员的集成权重的方法如式(16)所示：

其中，ωt表示聚类成员ct的聚类集成权重。

该方法所述步骤s50中计算数据集x中两个样本的加权相似性如式(17)所示：

其中，sim(xi,xj)表示样本xi和xj之间的加权相似性，按照这一方法计算数据集x中任意两个样本的加权相似性。

该方法所述步骤s60包含：

s61、构建数据集x的加权相似性矩阵θ＝[θ(xp,xq)]n×n，其矩阵元素θ(xp,xq)的计算方

法如式(18)所示：

其中参数γ的取值为sim(xi,xj)的标准差；

s62、将聚类集成任务转换为图最小分割问题，构建目标函数如式(19)所示：

该方法所述步骤s70包含：

s71、利用加权相似性矩阵θ每一列上元素之和构建一个n维对角矩阵，记为d，并定义矩阵l＝d-θ；

s72、求出矩阵l按从小到大顺序排列的前s*个特征值以及对应的特征向量

s73、将s*个特征向量排列在一起组成一个n×s*的矩阵，将其中每一行看作s*维空间中的一个向量，并使用k-means算法进行聚类，聚类结果中每一行所属的簇就是数据集x中每个样本数据所属的簇。

本发明针对聚类集体中的各个聚类成员质量参差不齐而对聚类集成产生不利影响的问题，提出了一种基于加权相似性度量的聚类集成方法，首先计算数据集中任意两个样本在每个聚类成员中对符号空间数据描述的一致性，接着计算每个聚类成员对特征空间数据描述的一致性并以此计算每个聚类成员的集成权重，在此基础上计算数据集中任意两个样本的加权相似性，然后构建数据集的加权相似性矩阵从而将聚类集成任务转换为图最小分割问题，通过利用谱聚类方法求解获得聚类集成结果，最终进行结果输出。本发明的主要参数包括：聚类符号向量集合、聚类符号向量集合关于数据集的条件信息熵、聚类符号向量集合关于两个样本在某一个聚类成员中所属簇的条件信息熵、两个样本在某一个聚类成员中对符号空间数据描述的一致性、标准化数据集关于原数据集的条件信息熵、标准化数据集关于某个聚类成员的条件信息熵、聚类成员对特征空间数据描述的一致性、聚类成员的集成权重、两个样本间的加权相似性、加权相似性矩阵。其中，聚类符号向量集合为符号空间中一系列对数据集进行符号描述的聚类符号向量构成的集合；聚类符号向量集合关于数据集的条件信息熵用于表示利用数据集x对符号空间数据描述的不确定性；聚类符号向量集合关于两个样本在某一个聚类成员中所属簇的条件信息熵用于表示利用这两个簇对符号空间数据描述的不确定性；两个样本在某一个聚类成员中对符号空间数据描述的一致性表示聚类符号向量集合关于数据集的条件信息熵以及关于两个样本在某一个聚类成员中所属簇的条件信息熵之间的差值；标准化数据集关于原数据集的条件信息熵用于表示利用数据集对特征空间数据描述的不确定性；标准化数据集关于某个聚类成员的条件信息熵用于该聚类成员对特征空间数据描述的不确定性；聚类成员对特征空间数据描述的一致性表示标准化数据集关于原数据集的条件信息熵与关于这个聚类成员的条件信息熵之间的差值；聚类成员的集成权重用于控制各聚类成员对最终聚类集成结果的影响；两个样本间的加权相似性用于描述两个样本在一系列聚类成员中簇划分的相似性；加权相似性矩阵用于描述数据集内部所有样本间簇划分的相似性情况。

本发明的有益效果在于：利用信息熵对数据描述中的一致性进行度量，以此计算聚类成员的聚类集成权重，利用加权相似性表达两个样本在一系列聚类成员中簇划分的相似性情况，将聚类集成任务转化为图最小分割问题，并通过谱聚类方法求解，该方法在构建数据集相似性矩阵时充分考虑了不同质量的聚类成员对聚类集成结果的影响，能够使最终获得的聚类集成结果更具准确性和鲁棒性。

附图说明

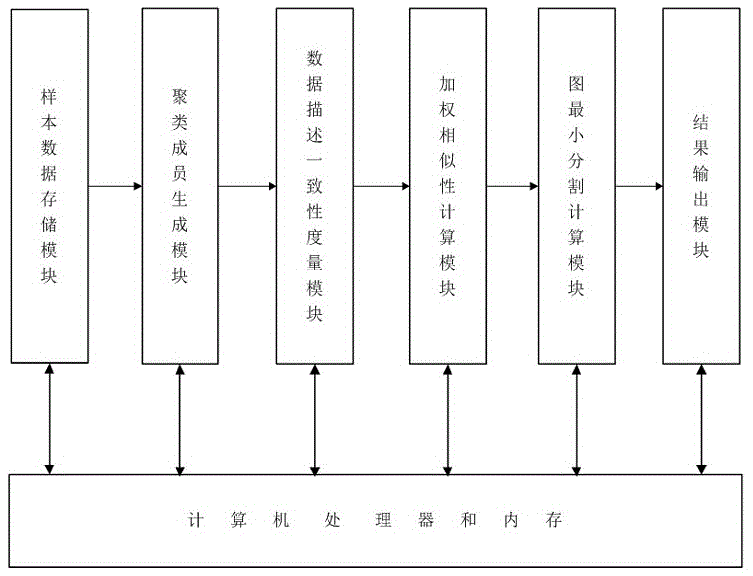
图1为本发明所述基于加权相似性度量的聚类集成方法的计算机实现系统结构图；

图2为本发明所述基于加权相似性度量的聚类集成方法的流程图。

具体实施方式

下面结合附图对本发明的具体实施方式进行详细说明。

本发明所述的基于加权相似性度量的聚类集成方法通过计算机程序实施，图1所示是计算机实现的系统结构图。下面将本发明提出的技术方案用于处理遥感图像数据，对遥感图像进行自动分类，实现地物目标的识别，输入数据为像素点构成的图像数据集，通过聚类集成方法将具有相似光谱特征的像素点归为一类，识别为同一地物目标，最终将识别出的各种地物目标进行输出，具体实施流程如图2所示。将遥感图像中每个像素点的光谱特征作为一个样本，数量为n的样本构成图像数据集在特征空间中x内的第i个样本记为xi；表示一系列在数据集x上生成的聚类成员构成的集合，即一系列像素点划分结果，其中t表示c中聚类成员的数量，表示第t个聚类成员，即对图像数据集的第t个划分结果，ct,k为ct中的第k个簇，即ct中的第个划分类别，st表示ct中簇的数量；将聚类划分视为对数据集的符号表示，那么聚类集合中每个聚类成员对应一个符号空间中的聚类符号向量，t个聚类符号向量构成的集合记为其中表示第t个聚类成员ct的聚类符号向量，lt,k表示ct中的第k个簇的标签；表示聚类集成结果，即最终的集成分割结果，其中c*,s表示c*中第s个簇，s*表示c*中簇的数量。本实施例即利用图像数据集x的一系列像素点划分结果生成一致的地物目标识别结果c*的过程，包括以下关键内容：

步骤1、对数据集进行数据标准化处理，利用式(1)所示的高斯核函数对特征空间中的数据集进行映射，使映射后得到的数据集服从高斯分布，其中ψi表示标准化数据集中的第i个样本；

其中，参数α的取值设为||xi-xo||²的标准差，xo为数据集x中的第o个样本(i≠o)，ψo为标准化数据集ψ中的第o个样本。

步骤2、计算数据集中任意两个样本在每个聚类成员中对符号空间数据描述的一致性：首先，计算聚类符号向量集合l关于数据集x的条件信息熵，用于表示利用数据集x对符号空间数据描述的不确定性；接着，计算聚类符号向量集合l关于两个样本在某一个聚类成员中所属簇的条件信息熵，用于表示利用这两个簇对符号空间数据描述的不确定性；再计算聚类符号向量集合l的以上两个条件信息熵的差值作为两个样本在这个聚类成员中对符号空间数据描述的一致性，以此类推计算任意两个样本在每个聚类成员中对符号空间数据描述的一致性，具体包含以下步骤：

s21、利用式(2)计算聚类符号向量集合l关于数据集x的条件信息熵，用于表示利用数据集x对符号空间数据描述的不确定性：

其中，h(lt|x)为第t个聚类成员ct的聚类符号向量lt关于数据集x的条件信息熵，可由式(3)计算：

其中，p(lt,k|x)表示聚类符号向量lt关于数据集x的条件概率，可由式(4)计算：

式中xi(lt)表示样本xi在第t个聚类符号向量上的取值，即样本xi在第t个聚类成员中对应的簇标签；

s22、对于数据集x中的任意两个样本xi和xj，它们在第t个聚类成员ct中所属的簇分别为和利用式(5)计算聚类符号向量集合l关于这两个簇的条件信息熵，用于表示利用这两个簇对符号空间数据描述的不确定性：

其中，为和构成的集合，为第t个聚类成员ct的聚类符号向量lt关于集合的条件信息熵，可由式(6)计算：

其中，表示聚类符号向量lt关于集合的条件概率，可由式(7)计算：

式中xd(lt)表示样本xd在第t个聚类符号向量上的取值，即样本xd在第t个聚类成员中对应的簇标签；

s23、计算聚类符号向量集合l关于数据集x的条件信息熵与关于的信息熵的差值作为样本xi和xj在聚类成员ct中对符号空间数据描述的一致性，如式(8)所示：

s24、利用步骤s21～s23的方法，计算数据集x中全部两个样本在每个聚类成员中对符号空间数据描述的一致性。

步骤3、计算每个聚类成员对特征空间数据描述的一致性：首先，计算标准化数据集ψ关于数据集x的条件信息熵，用于表示利用数据集x对特征空间数据描述的不确定性；接着，计算数据集ψ关于某个聚类成员的条件信息熵，用于表示该聚类成员对特征空间数据描述的不确定性；计算数据集ψ的以上两个条件信息熵的差值作为该聚类成员对特征空间数据描述的一致性，以此类推计算每个聚类成员对特征空间数据描述的一致性，具体包含以下步骤：

s31、利用式(9)计算标准化数据集ψ关于数据集x的条件信息熵，用于表示利用数据集x对特征空间数据描述的不确定性

其中，h(ψ|x)为标准化数据集ψ关于数据集x的条件信息熵，表示标准化数据集ψ的方差，由式(10)进行计算：

其中，μψ为标准化数据集ψ的期望，满足式(11)：

s32、计算标准化数据集ψ关于每个聚类成员的条件信息熵，用于描述各聚类成员对特征空间数据描述的一致性，其中ψ关于第t个聚类成员ct的条件信息熵可由式(12)计算：

其中，h(ψ|ct)为标准化数据集ψ关于第t个聚类成员ct的条件信息熵，表示ct中样本的方差，由式(13)进行计算：

其中，为ct中样本的期望，满足式(14)：

式中，ψe为标准化数据集ψ中的第e个样本，xe为数据集x的第e个样本，xf为数据集x的第f个样本(e≠f)，xg和xh为数据集x中不相同的任意两个样本；

s33、计算标准化数据集ψ的以上两个条件信息熵的差值，作为该聚类成员对特征空间数据描述的一致性，其中第t个聚类成员ct在ψ上的一致性度量由式(15)计算：

i(ψ|ct)＝h(ψ|x)-h(ψ|ct)(15)

其中，i(ψ|ct)表示ct在ψ上的一致性度量；

s34、利用步骤s31～s33的方法，逐个计算每个聚类成员对特征空间数据描述的一致性。

步骤4、依据每个聚类成员对特征空间数据描述的一致性计算每个聚类成员的集成权重，分别控制各聚类成员对最终聚类集成结果的影响，其中聚类成员ct的聚类集成权重ωt的计算方法如式(16)所示：

步骤5、利用步骤s20获得的任意两个样本在每个聚类成员中对符号空间数据描述的一致性以及步骤s40获得的每个聚类成员的集成权重计算数据集中任意两个样本的加权相似性，其中xi和xj之间的加权相似性sim(xi,xj)的计算方法如式(17)所示：

步骤6、将聚类集成任务转换为图最小分割问题，即使得最终的聚类集成结果中所有不在同一簇中的两个对象间的加权相似性最小，具体包含以下步骤：

s61、构建数据集x的加权相似性矩阵θ＝[θ(xp,xq)]n×n，其矩阵元素θ(xp,xq)的计算方法如式(18)所示：

其中参数γ的取值为sim(xi,xj)的标准差；

s62、将聚类集成任务转换为图最小分割问题，构建目标函数如式(19)所示：

步骤7、利用谱聚类方法对聚类集成任务转换得到的图最小分割问题进行求解，获得聚类集成结果c*，具体包含以下步骤：

s71、利用加权相似性矩阵θ每一列上元素之和构建一个n维对角矩阵，记为d，并定义矩阵l＝d-θ；

s72、求出矩阵l按从小到大顺序排列的前s*个特征值以及对应的特征向量

s73、将s*个特征向量排列在一起组成一个n×s*的矩阵，将其中每一行看作s*维空间中的一个向量，并使用k-means算法进行聚类，聚类结果中每一行所属的簇就是数据集x中每个样本数据所属的簇。

步骤8、将聚类集成结果c*即地物目标识别结果进行输出，结果中的每个簇表示一个识别出的地物目标。