一种基于数独分组的扩展平移拉丁超立方试验设计方法与流程

本发明属于仿真试验设计领域，涉及一种试验样本空间设计方法，具体涉及一种基于数独分组的扩展平移拉丁超立方试验设计方法。

背景技术：

在武器系统对抗条件下，不同的武器系统装备数据和战术方法会影响最终的对抗效果，需要对这些影响因子选取不同的参数组合，进行多次试验，以得出最优的武器系统技术指标和战术途径。然而，进行多次真实场景试验需要大量人力物力，因此常通过大量仿真样本的运行结果来获得对问题的全局理解。虽然计算机硬件能力一直在快速增长，但是多数情况下将仿真场景中所有可能出现的情况全部执行一遍是不现实的。经济与科学地获得影响因子水平采样点，根据样本空间安排试验是仿真试验设计的主要目的，近年来，采用拉丁超立方设计方法进行样本空间设计来安排试验，成为实验设计中较热门的研究领域。

基本的拉丁超立方设计是指任意二维子空间的每行每列都只能有一个样本，试验次数等于水平数，采用随机抽样，其随机性取决于计算机的随机数产生器，具有不稳定的表现。为了优化基本拉丁超立方的正交性与均匀性，发展出通过相关系数表控制非正交性、使用遗传算法迭代优化等方法。最优的拉丁超立方设计搜索复杂度为(n！)^m，十分耗时，扩展平移拉丁超立方通过空间复制平移，能够快速地生成近似最优的拉丁超立方设计。由于扩展平移拉丁超立方只有在6维及以下才有好的效果，因此不适用于维度>6的试验设计问题。

数独矩阵是一种特殊的拉丁超立方，其行数和列数均可表示为m²(m为大于等于2的整数)，每行/列中1,2,...,m²各只出现一次，且分成m²个m×m的子块时，每个子块中填充有数列集{1,2,...,m²}中的数字，并保持行和列的均匀性。

武器系统对抗模型需要综合考虑多个因子(因子数＞＞6)的影响，扩展平移拉丁超立方设计无法取得因子的某些水平，因此试验结果不具备代表性，需要一种能快速生成近似最优拉丁超立方的设计方法，为武器系统对抗仿真试验提供具有代表性的样本空间。

技术实现要素：

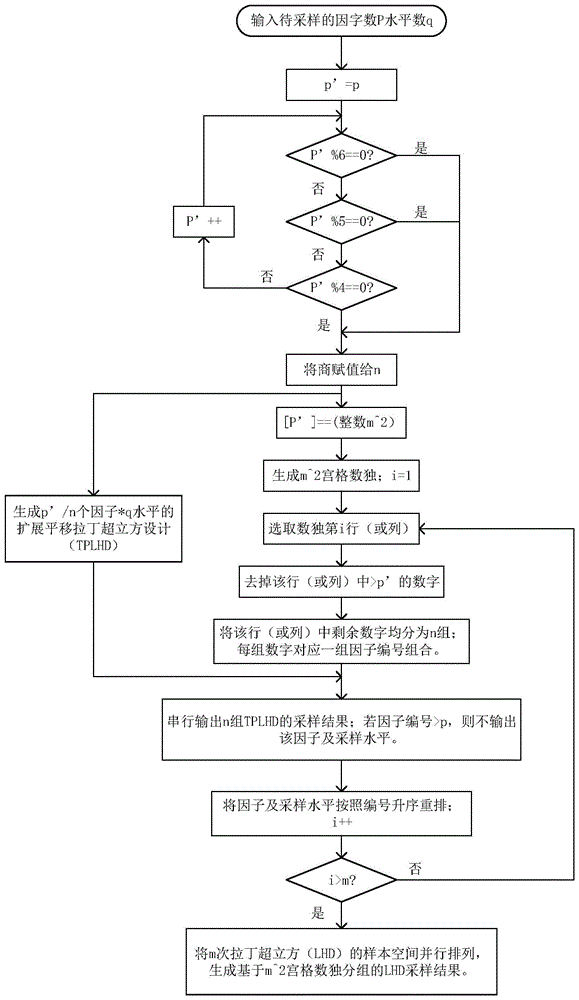
本发明是一种基于仿真试验的试验样本空间设计方法，所述的试验样本空间设计方法，采用扩展平移拉丁超立方试验设计方法，结合数独矩阵的分布均匀性，在维度<6的扩展平移拉丁超立方设计已知的情况下，提出维度>6的多因子扩展平移拉丁超立方设计方法。本发明所述方法首先计算得到因子分组情况；根据每组因子个数生成扩展平移拉丁超立方设计；根据因子数生成数独，数独中数字对应因子编号；删除数独中多余因子编号，取若干行/列进行分组；每组因子根据已生成的拉丁超立方设计输出采样结果，每行/列的各组因子的采样结果按编号升序串行排列，各行/列的采样结果并行排列，组合成最终的基于数独分组的扩展平移拉丁超立方样本空间。

本发明提供的基于数独分组的扩展平移拉丁超立方试验设计方法，具体包括以下几个步骤：

步骤一、针对某多个因子的扩展平移拉丁超立方试验设计，将其因子平均分组。

具体步骤如下：

步骤101、将因子数p赋值给p’。

步骤102、判断p’能否被6整除，如果能，将商赋值给n，进入步骤二；如果不能，进入步骤103。

步骤103、判断p’能否被5整除，如果能，将商赋值给n，进入步骤二；如果不能，进入步骤104。

步骤104、判断p’能否被4整除，如果能，将商赋值给n，进入步骤二；如果不能，将p’加1，进入步骤102。

步骤二、生成单组扩展平移拉丁超立方试验设计。

具体步骤如下：

步骤201、生成p’/n个因子的扩展平移拉丁超立方试验设计。每个因子对应一个采样结果。

步骤三、根据因子数生成对应数独。

具体步骤如下：

步骤301、p’向上取整到最近的整数m的平方数；

步骤302、生成m²宫格数独。

步骤四、数独分组，生成最终的拉丁超立方试验设计。

具体步骤如下：

步骤401、选取数独第一行/列；

步骤402、去除该行/列中大于p’的数字；

步骤403、将该行/列中剩余数字按原来顺序平均分为n组，数字与因子编号相对应，则n组数字对应n个因子组合；

步骤404、根据步骤201中生成的超立方试验设计，分别输出n组因子的采样结果，如果某组中某因子编号>p，则不输出该因子的采样结果；

步骤405、将n组采样结果串行组合，并按因子编号升序重新排列，生成一次拉丁超立方试验设计；

步骤406、取后一行/列，进入步骤402；重复进行m次。

步骤407、将m次拉丁超立方设计并行组合，生成基于m²宫格数独的扩展平移拉丁超立方实验样本空间。

本发明优点在于：

(1)本发明一种基于数独分组的扩展平移拉丁超立方试验设计方法，对于多因子采样空间设计问题，该方法相较于扩展平移拉丁超立方设计，用时短，生成样本点数少，有效减少仿真试验时间。

(2)本发明实现将多因子采样问题划分为若干组因子数<6的拉丁超立方采样问题，相较于扩展平移拉丁超立方设计方法，本发明所得的样本空间更接近最优拉丁超立方设计，样本点分布更均匀，使得仿真试验结果更具备代表性。

(3)本发明一种基于数独分组的扩展平移拉丁超立方试验设计方法，利用数独空间分布均匀性，降低因子之间的相关性，解决因子分组造成的混杂问题。

附图说明

图1是本发明一种基于数独分组的扩展平移拉丁超立方试验设计方法流程图；

图2是本发明随机生成的16宫格数独分组流程；

图3是本发明实施例中基于16宫格数独分组拉丁超立方样本空间中因子排列情况；

图4是本发明生成单弹突防能力样本空间中前10个样本采样点。

具体实施方式

下面结合附图对本发明的具体实施方法进行详细说明。

本发明针对现有扩展平移拉丁超立方试验设计问题，提出了一种基于数独分组的扩展平移拉丁超立方试验设计新方法。所述方法首先将因子平均分组，生成单组扩展平移拉丁超立方试验设计；因子数向上取整到最近的某整数的平方数，生成该整数宫格的数独，数独中数字对应因子编号；选取数独前宫格数行/列，将选取的每一行/列删除多余因子编号，按因子分组数平均分组；将每组因子按照已生成的拉丁超立方设计输出采样结果，每行/列的各组采样结果串行组合并按因子编号升序重新排列；将选取的宫格数行/列对应的采样结果并行组合，生成最终的基于数独分组的扩展平移拉丁超立方样本空间。

本发明提供一种基于数独分组的扩展平移拉丁超立方试验设计方法，针对武器系统对抗条件，本发明对单枚导弹突防能力进行试验样本空间设计。如图1所示流程，图1中运算符号说明：/整除运算符；％取余运算符；[]向上取整运算符；^幂运算符号；*乘法运算符。具体步骤如下：

步骤一、针对某多个因子的扩展平移拉丁超立方试验设计，将其因子平均分组。

单弹突防能力模型中，导弹突防能力的影响因子共13个，依次编号为01～13，每个影响因子可取5个水平，如表1所示：

表1导弹突防能力的影响因子和因子水平

具体包括以下几个步骤：

步骤101、将因子数p赋值给p’。

步骤102、判断p’能否被6整除，如果能，将商赋值给n，进入步骤二；如果不能，进入步骤103。由于本发明中导弹突防能力的影响因子共13个，因此不能被6整除，进入步骤103。

步骤103、判断p’能否被5整除，如果能，将商赋值给n，进入步骤二；如果不能，进入步骤104。

步骤104、判断p’能否被4整除，如果能，将商赋值给n，进入步骤二；如果不能，将p’加1，进入步骤102。

根据导弹突防能力的影响因子共13个，第一次需要加1，还是不能整除，继续加1，数字p’＝15可以被5整除，将n赋值n＝3，进入步骤二。

步骤二、生成单组扩展平移拉丁超立方试验设计。

生成p’/n＝5个因子×5水平的的扩展平移拉丁超立方试验设计。

步骤三、根据因子数生成对应数独。

具体步骤如下：

步骤301、p’＝15在向上取整到最近的整数m＝4的平方数4²＝16；

步骤302、生成m²＝16宫格数独。

步骤四、将16宫格数独分组，生成最终的拉丁超立方试验设计(lhd)。

如图2所示，具体步骤如下：

步骤401、选取数独第一行/列；

步骤402、去除该行/列中大于p’＝15的影响因子；

步骤403、将该行/列中剩余影响因子按原来顺序平均分为n＝3组，影响因子与因子编号相对应，则n组数字对应n个影响因子组合；

步骤404、根据步骤二中生成的超立方试验设计，分别输出n组影响因子的采样结果，如果某组中某影响因子编号>p，p为因字数，则不输出该因子的采样结果；如图2，编号大于13的因子不输出。取下一行，重复上述步骤共4次，最终得到前4行对应的采样结果。

步骤405、将每行中n组采样结果串行排列组合，并按影响因子编号升序重新排列，如图3，生成一次拉丁超立方试验设计；

步骤406、取后一行/列，进入步骤402；重复进行m次。

步骤407、将m次拉丁超立方设计并行组合，生成基于m²宫格数独的扩展平移拉丁超立方试验设计(tplhd)。

将4行对应的采样结果并行排列，作为最终的基于16宫格数独分组对13因子×5水平的采样问题进行扩展平移拉丁超立方试验设计结果；生成的采样空间中共包含116个样本点，其中前10个样本点如图4所示。

基于以上步骤实现了对任意的影响因子数>6的多因子采样问题，计算得到因子分组情况，生成单组扩展平移拉丁超立方设计，生成数独并基于数独分组输出最终的扩展平移拉丁超立方样本空间。

根据此样本空间设计进行单枚导弹突防能力试验，可以有效减少试验样本个数，进而节约计算机仿真试验时间；与原始的扩展平移拉丁超立方样本空间相比，此样本空间中样本点覆盖更均匀，使仿真试验结果更具备可信性。