考虑日周期性影响的光伏功率爬坡事件非精确概率预测方法及系统与流程

本发明涉及光伏功率爬坡事件技术领域，尤其涉及一种考虑日周期性影响的光伏功率爬坡事件非精确概率预测方法及系统。

背景技术：

本部分的陈述仅仅是提供了与本发明相关的背景技术信息，不必然构成在先技术。

近年来可再生能源发电快速发展，在电网中的渗透率不断提高，在有效缓解环境污染与资源危机的同时，因其固有的随机性与波动性，也对电网的安全稳定运行提出了挑战。特别是光伏电站的功率爬坡事件，即输出功率短时间内的大幅度波动，可能导致电网功率平衡的破坏，引发系统频率波动，甚至造成严重的停电事故。为此，提高对光伏发电爬坡事件的预测能力将为电网及时有效地制定调度与控制决策、维持电网稳定运行创造条件，是保证光伏高渗透率电网频率稳定的必备措施。

目前，对于光伏功率爬坡事件的研究尚处于起步阶段，对于其定义也尚未达成共识。现有研究多将光伏爬坡特征量超过设定阈值定义为光伏爬坡事件，该特征量可以是一定时间段内开始与结束时刻的功率之差，也可以是一定时间内光伏输出最大功率与最小功率之差，或是多个时段的累积功率变化量。这些定义方法描述爬坡事件时普遍存在忽视光伏发电日趋势性变化的问题，即没有考虑光伏发电所具有的明显的日周期性。因此，若阈值设定不当，这些爬坡定义方法将有可能导致不必要的连续爬坡警报。

发明人发现，现有的光伏发电爬坡事件预测方法可大致分为间接预测法和直接预测法两类。间接预测法首先进行发电功率的预测，随后在功率序列中利用设定的标准，进行爬坡事件的识别。但是，此类预测方法在进行功率序列预测时，为了降低整体预测误差，往往会忽略极端样本，忽视功率的突变，从而导致爬坡信息的损失，引发爬坡事件的漏报。与之相比，直接预测法则不进行功率预测，而是直接在相关因素与爬坡事件之间建立起映射关系，具有较好的爬坡事件捕捉与识别能力。

从预测原理上看，爬坡事件的研究既可以从机理分析入手，也可以基于数据统计。机理建模抓住了爬坡发生的根本原因，却常忽略实际发电过程中的多种因素的影响，不仅分析过程复杂且结果常与实际不符。将机理建模与数据驱动有效结合将在提供物理依据的同时，提高预测方法的适用性。样本充足(即大数定理成立)的前提下，爬坡事件可以得到可靠的概率分布，以精确概率来预测。而事实上，受气象因素影响的爬坡事件发生几率相对较低，某些气象条件很少发生，导致相关样本较少，不可避免的在概率预测中引入误差。

技术实现要素：

针对现有光伏发电功率爬坡事件预测存在不当警报的问题，本发明提出了一种考虑日周期性影响的光伏功率爬坡事件非精确概率预测方法及系统，可有效避免爬坡事件样本不足而导致的概率预测误差，为电网运行调度提供更为全面的决策信息。

为了实现上述目的，本发明采用如下技术方案：

在一个或多个实施方式中，公开了一种考虑日周期性影响的光伏功率爬坡事件非精确概率预测方法，包括：

获取光伏电站输出功率数据与光伏电站所在位置的气象数据，作为样本数据；

定义光伏功率相对爬坡率，对样本数据进行预处理，构建信度网络节点变量集与各节点变量的状态集；

利用贪婪搜索算法构造样本数据下光伏发电爬坡预测的最优信度网络结构；

统计历史数据中不同爬坡状态的先验概率，利用idm估计各信度网络节点关联的非精确条件概率，构造条件信度集；

进行光伏发电爬坡的信度网络概率推理，得到给定气象条件下的光伏功率爬坡概率的非精确预测结果。

进一步地，构建信度网络节点变量集与各节点变量的状态，具体为：

信度网络的根节点变量为光伏爬坡状态，选取影响光伏功率爬坡的光照幅度爬坡状态、光照幅度、环境温度、气压和相对湿度构成信度网络节点证据变量集；

根据光伏功率相对爬坡率划分光伏爬坡状态，根据光照幅度相对爬坡率划分光照幅度爬坡状态，根据光照幅度值、环境温度值、气压值和相对湿度值分别作为信度网络节点证据变量光照幅度、环境温度、气压和相对湿度的划分依据。

进一步地，所述光伏功率相对爬坡率具体为：

光伏发电功率在相邻时段间的变化幅度与由晴空模型估计得到的光伏发电功率在相邻时段间的变化幅度之差，与相邻时间段的时间间隔的比值。

进一步地，利用贪婪搜索算法构造样本数据下光伏发电爬坡预测的最优信度网络结构，具体为：

设定初始信度网络结构；

搜索算子根据dag原理对当前结构进行局部更新；

以评分函数评估所有候选结构和当前结构；

如果最优候选结构优于当前结构，以最优候选结构替代当前结构，重新对当前结构进行局部更新；否则，输出当前结构为最优结构。

进一步地，利用idm估计各爬坡证据节点关联的非精确条件概率，具体为：

采用先验概率密度函数的集合来进行估计，该集合由给定s条件下所有的dirichlet分布构成，即在固定s值后，使r遍历整个[0,1]区间；

根据贝叶斯原理，将θ的先验概率密度函数集合更新为后验概率密度函数集合，从而，获得概率θ的取值区间。

进一步地，概率θ的取值区间具体为：

其中，s为设定参数表征为对新信息的慎重程度，r为超参数，θ为随机变量；m＝{m1,m2,…,mn}为样本观测；mi表示随机变量状态i的出现次数；m＝m1+m2+…+mn为样本总数；s为设定参数表征为对新信息的慎重程度。

进一步地，进行光伏发电爬坡的信度网络概率推理，得到给定气象条件下的光伏功率爬坡概率的非精确预测结果，具体为：

对于具有n个节点的光伏爬坡信度网络，x＝(x1,x2,…,xn)是n维随机变量x＝{x1,x2,…,xn}的一组状态；利用贝叶斯网络推理手段，遍历信度集顶点组合成的联合概率质量函数完成对信度网络的精确推理；计算根节点变量r的状态ri在气象证据变量e的观察值xe下出现概率p(ri|xe)的最大、最小边界值。

进一步地，根节点变量r的状态ri在气象证据变量e的观察值xe下出现概率p(ri|xe)的最大、最小边界值，具体为：

其中，k(x)为条件信度集；p(x)∈ext[k(x)]表明p(x)应从随机变量条件信度集顶点对应的概率质量函数上取值；xm1为节点变量集合x\{r,e}；xm2为节点变量集合x\e；∑xm表示对节点变量集合xm的全概率运算，pj(xi|πi)为条件质量函数集。

在一个或多个实施方式中公开的一种考虑日周期性影响的光伏功率爬坡事件非精确概率预测系统，包括服务器，所述服务器包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现权利要求1-8任一项所述的方法。

在一个或多个实施方式中公开的一种计算机可读存储介质，其上存储有计算机程序，该程序被处理器执行时执行上述的方法。

与现有技术相比，本发明的有益效果是：

采用新提出的光伏发电功率爬坡特征量，完成对由于受到特殊气象变动影响而造成的意外功率变动的有效捕捉，同时充分考虑光伏发电爬坡事件预测时可能存在的样本不足问题，提出了基于信度网络和非精确狄利克雷模型的光伏发电爬坡事件的非精确概率预测方法。从而，利用所构建的模型，依据数值天气预报，可实现对光伏发电爬坡事件发生概率的区间预测。仿真分析表明，本发明方法可有效避免爬坡事件样本不足而导致的概率预测误差，为电网运行调度提供更为全面的决策信息。

附图说明

构成本申请的一部分的说明书附图用来提供对本申请的进一步理解，本申请的示意性实施例及其说明用于解释本申请，并不构成对本申请的不当限定。

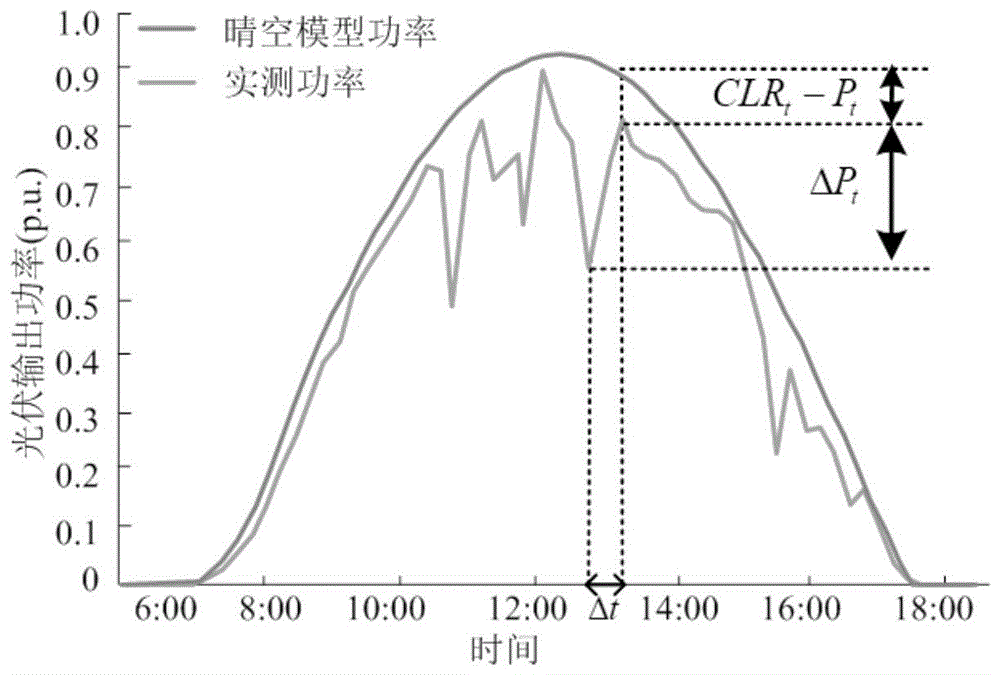
图1为实施例一中相对爬坡率示意图；

图2为实施例一中简单三点信度网络结构示意图；

图3为实施例一中贪婪搜索算法结构学习流程图；

图4为实施例一中光伏功率爬坡概率估计信度网络示意图；

图5为实施例一中在6种不同气象条件下光伏爬坡事件非精确概率；

图6为实施例一中连续时段光伏功率下爬坡事件非精确/单值概率。

具体实施方式

应该指出，以下详细说明都是示例性的，旨在对本申请提供进一步的说明。除非另有指明，本发明使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。

需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。

实施例一

在一个或多个实施方式中公开了一种考虑日周期性影响的光伏功率爬坡事件非精确概率预测方法，包括：

获取样本数据；样本数据包括：待测光伏电站输出功率数据与光伏电站所在位置的气象数据(温度、太阳辐射度、湿度、气压等)；

定义光伏功率相对爬坡率，对样本数据进行预处理，构建信度网络节点变量集与各节点变量的状态集；

利用贪婪搜索算法构造样本数据下光伏发电爬坡预测的最优信度网络结构；

统计历史数据中不同爬坡状态的先验概率，利用idm估计各爬坡证据节点关联的非精确条件概率，构造条件信度集；

进行光伏发电爬坡的信度网络概率推理，得到给定气象条件下的光伏功率爬坡概率的非精确预测结果。

下面对上述方法进行进一步说明：

1电网光伏发电功率爬坡特征量及其分析

光伏发电功率变化与两类因素有关，一类是由地球自转公转引发的规律性昼夜波动；另一类是由气象条件的突然变动(如云团移动等)导致的光伏发电的非规律性变动。现有光伏爬坡事件定义中常采用的光伏爬坡特征量有时段内功率变化量δp、时段内功率最大值与最小值之差时段内功率变化率rate还有对功率进行预处理后的滤波信号pt^f，分别如式(1)-式(4)所示。

δp(t)＝p(t+δt)-p(t)(1)

pt^f＝mean(pt+h-pt+h-n),h＝1,2,...,n(4)

式中，p(t)为t时刻输出功率；p[t,t+δt]为时段内功率集；h为滤波信号时间窗宽；pt^f为功率滤波信号。

采用以上特征量的光伏爬坡事件定义不仅存在无法识别时间段内功率变化过程、不易区分爬坡方向等缺陷，更重要的，这些定义均不加区分地将两类功率变动影响因素视为一体，这将在爬坡阈值设置不当时引发不必要的持续爬坡报警。

为此，提出一种新的光伏发电爬坡特征量，即相对爬坡率(rrr)指标：

式中，pt为t时刻光伏发电的实测功率；clrt为晴空模型计算得到的t时刻的光伏发电功率；δt为间隔时长。

这其中，晴空模型是一种常用的光伏发电的估计方法，其结合了晴空指数与光伏发电系统的数学模型，以经纬度、时间、平均linke浊度系数和光伏电站装机容量作为模型的输入[14,^15]，对标准温度和气压及晴空(即无遮挡)条件下光伏的发电功率进行预测。图1为相对爬坡率示意图。由图可见，晴空模型的功率曲线相对平滑，反映的是未考虑气象突变的日趋势性功率变动。

根据式(5)，容易得到相对爬坡率的另一种表达形式，即：

式中，δpt＝pt-pt-1是光伏发电功率在相邻时段间的变化幅度；δclrt＝clrt-clrt-1为由晴空模型估计得到的光伏发电功率在相邻时段间的变化幅度。

在光伏日周期性对功率变动影响较大的时间段(即临近日出或日落的数小时内)，设定统一爬坡阈值，按照式(1)-式(4)所示的光伏爬坡事件定义方法识别出的爬坡事件具有明显的时间分布特征：即上爬坡事件将集中在上午时段，下爬坡事件集中发生在下午时段。比较而言，采用相对爬坡率进行爬坡识别具有以下优势。

(1)降低了光伏发电爬坡事件的误报率：将晴空模型预测功率序列作为光伏电站发电计划，式(1)-式(4)所示爬坡特征量识别出的多数爬坡事件是意料之中的(如图1中8:00-10：00时段)，因此产生的爬坡事件警报多为无效警报，即爬坡误报。而采用相对爬坡率进行识别时，由日周期性引起的功率变动将不会被识别爬坡事件。

(2)降低了光伏发电爬坡事件的漏报率：如图1中10:15-10:30时段，光伏电站输出功率值变动不大却与计划发电曲线有较大偏离，依据现有光伏爬坡事件定义将被视为无爬坡事件发生，由此引发爬坡漏报。而相对爬坡率则能将其识别为偏离了计划曲线的下爬坡事件。可见，相对爬坡率提高了爬坡识别的敏锐度。

(3)便于与电网调度决策进行配合：发电计划制定一般以晴空模型功率作为基准，相对爬坡率的提出，有利于对应系统功率调节手段进行爬坡阈值分级设定，以此实现光伏发电爬坡的分级预警，即满足不同电网的差异化需求，同时又能为电网调度提供更精细化的信息。

综上，通过将晴空模型加入分析，相对爬坡率这一特征量能够有效地剔除光伏发电功率中的日趋势性变动，从而捕捉到由非规律性气象变动而导致的功率突变，提高了对光伏发电爬坡有效识别的能力。显然，与晴空模型所得理想包络线突然的大幅偏离是电网运行调度人员所更加关心的。

2非精确关联条件概率的建立

光伏发电爬坡与多种气象因素相关，某些特殊气象条件，历史上发生的次数不多，因此在对这些气象条件与光伏发电爬坡事件进行关联性估计时，可用样本不足，难以获得精确的单值概率统计结果。要实现对于这类多项式分布数据的客观统计推理，相较于对样本容量要求较高的中心极限定理(clt)，非精确狄利克雷模型通过采用先验概率密度函数集合，可得到小样本条件下的非精确概率，已成功用于输电线路故障诊断、机组组合优化等场景。

idm是确定性dirichlet模型的扩展。设服从多项式分布的随机变量具有n种可能出现的状态，其各状态发生的概率以θ＝(θ1,θ2,…,θn)表示。确定性dirichlet模型借助贝叶斯统计原理，视未知参数θ为随机变量，采用dirichlet分布作为其先验概率密度函数。进而，在获取到样本观测值m的条件下，经贝叶斯过程更新形成后验dirichlet概率密度函数，如式(7)所示。

式中：γ(·)表示gamma函数；ri为超参数，满足0≤ri≤1及和为1约束，其代表了θi的均值；s为设定参数表征为对新信息的慎重程度，通常在[1,2]之间取值。m＝{m1,m2,…,mn}为样本观测；mi表示随机变量状态i的出现次数；m＝m1+m2+…+mn为样本总数。然而，确定性dirichlet概率估计方法对小样本事件存在受先验分布影响显著的弊端，当先验信息设置不合理时，易得到不可靠的估计结果。

为了避免这一弊端，idm采用先验概率密度函数的集合而非单一概率密度函数来进行估计，该集合由给定s条件下所有的dirichlet分布构成，即在固定s值后，使r遍历整个[0,1]区间。进而，可以根据贝叶斯原理，将θ的先验概率密度函数集合更新为后验概率密度函数集合，从而，获得概率θ的取值区间，如式(8)所示。

由此，可以根据小样本数据，方便地估计得到给定条件下随机变量状态出现的概率区间。易见，idm统计方法消除了在小样本条件下，先验设置不合理对事件发生概率估计的不利影响。显然，式(8)符合非精确概率的表达形式，即式(9)。

式中：pim(a)表示事件a发生的非精确概率；p(a)为非精确概率下界；为非精确概率上界，显然，p(a)与满足约束。

可以看出，对于式(9)所示的非精确概率，若则非精确概率将退化为精确的单值概率，这说明事件a发生的概率将是精确的。另一方面，若p(a)＝0，则代表该概率可能为由0至1区间内的任意值，说明事件a可用历史信息缺乏，通过现有信息难以给出有价值的概率统计结果。由此可见，非精确概率对各类气象因素下光伏发电功率爬坡事件发生的可能性具有更加全面、灵活的表达能力。

3基于信度网络的光伏爬坡事件预测

信度网络作为经典贝叶斯网络的拓展，是一种表达不确定性知识和进行因果推理的非精确概率图模型，其结构如图2所示。图中，若变量a为根节点，则节点b、c为a节点的证据变量。信度网络的节点与弧不一定需要具有精确的概率表达，而是可以具有非精确概率测度的表达形式。若信度网络中每个节点变量在给定其父节点条件下独立于它的非子孙、非父节点，则称该网络满足强马尔科夫条件，多数推理问题包括本发明所述的光伏功率爬坡事件概率的估计问题所对应的信度网络满足强马尔科夫条件。

光伏功率爬坡事件的发生与所处地区的天气状况密切相关，本发明选取影响光伏功率爬坡的光照幅度、环境温度、气压、相对湿度四类气象因素构成信度网络节点证据变量集e＝{ri,i,t,p,h}，信度网络的根节点变量为光伏爬坡状态r，各变量符号含义如表1所示。e中各节点证据变量按无监督准则中常用的等频原则划分为3个状态。根节点变量r则依据爬坡状态划分为爬坡状态集ri＝{r1,r2,r3}，其中，下爬坡为r1，不爬坡为r2，上爬坡为r3。

表1节点变量集

需要说明的是，光照幅度相对爬坡率采用与光伏功率相对爬坡率相同原则计算。

信度网络需进行结构学习，方可寻找出样本数据下的最优网络结构，以抽象表达各气象要素间的潜在依赖关系，最优结构的搜索过程如图3。本发明采用贪婪搜索算法对光伏功率爬坡概率预测的信度网络进行结构学习

寻得最优网络结构后，即可进行信度网络的结构推理。对于具有n个节点的光伏爬坡信度网络，x＝(x1,x2,…,xn)是n维随机变量x＝{x1,x2,…,xn}的一组状态。利用常规贝叶斯网络推理手段，遍历信度集顶点组合成的联合概率质量函数可以完成对信度网络的精确推理，计算根节点变量r的状态ri在气象证据变量e的观察值xe下出现概率p(ri|xe)的最大、最小边界值，如式(10)、(11)所示。

式中：k(x)为条件信度集；p(x)∈ext[k(x)]表明p(x)应从随机变量条件信度集顶点对应的概率质量函数上取值；xm1为节点变量集合x\{r,e}；xm2为节点变量集合x\e；∑xm表示对节点变量集合xm的全概率运算。

4算例分析

以新疆某光伏电站数据为例验证所提方法。选用2015-2017年电站实际运行功率数据，时间分辨率为15min，该光伏电站装机容量为90mw。经过合理性检验与筛选后，将数据划分为训练集、验证集，按照步骤(1)构造节点变量集{r,e}与变量状态集{ri,xe}，其中，xe＝{rim,in,ta,pb,hc}，i,m,n,a,b,c∈{1,2,3}。

4.1新特征量的有效性分析

本发明提出了新的爬坡特征量，现以训练集数据为例验证其对光伏爬坡事件的识别能力。以光伏电站装机容量的5％作为爬坡阈值，分别依据本发明提出的rrr以及前述和rate两类特征量，以气象变动引发的光伏发电爬坡事件为识别对象，对样本数据进行爬坡识别，三类方法下爬坡事件识别结果的统计见表2。

表2光伏发电爬坡事件识别结果

上表中，1为识别所得上爬坡与下爬坡事件件数之和；2为误报爬坡事件件数与识别所得爬坡总件数之比；3为漏报爬坡事件件数与实际气象引发的爬坡总件数之比。

从表2可以看出，采用相对爬坡率识别结果中爬坡事件数远少于其他两类爬坡特征量。并且针对最受关注的由气象变动引发的爬坡事件，其他两类特征量漏报率和误报率均较高，即对有价值的爬坡信息捕获准确率较低。而本发明提出的相对爬坡率则能够准确有效的识别目标爬坡事件，减少不必要的爬坡警报。

4.2信度网络构建与推理

光伏功率爬坡信度网络中各节点变量确定后，按照步骤(2)运用贪婪搜索算法不断对信度网络进行局部更新。本发明采用贝叶斯信息准则来评价网络结构的质量，该准则利用似然函数来描述结构与数据之间的拟合程度，惩罚结构的复杂性，避免过拟合。最终在172类网络结构中寻得最优信度网络结构如图4所示。

由构建的信度网络结构可知，光伏功率爬坡事件与光照幅度、湿度、温度以及光照幅度相对爬坡率直接相关。需要注意的是，图4中证据变量i、h由多个父节点共同影响，因此，在步骤(3)求取条件信度集时，需计及其所有父节点不同状态出现的情况，以光伏功率的长期统计爬坡概率替代各爬坡状态的先验概率。

依据步骤(3)得到各节点的概率关联后，按步骤(4)求解即可得到给定气象条件下各光伏功率爬坡状态rl(l∈{1,2,3})非精确条件概率pim(rl|ee)，即

4.3非精确概率估计结果

中心极限定理(clt)是一种常用的估计均值分布的统计方法，常作为非精确概率估计的对照方法。选取6个不同的气象场景，采用本发明方法和中心极限定理(90％置信区间)对不同气象状态组合下的各爬坡状态的发生概率进行估计，概率估计情况如图5所示。

图5中可以看到，在气象条件e1、e2、e3下，本发明方法和clt都可以有效的覆盖真实概率，但比较而言，clt模型估计所得的概率区间较本发明方法更宽，敏锐度较弱；在气象条件e4、e5下光伏功率爬坡样本数量较少，不同爬坡状态在训练集与验证集中的发生概率存在差异，此时不满足clt对样本数据大容量的要求，因此clt模型估计得到的概率区间无法准确的覆盖真实概率，但本发明方法仍可以用较为狭窄的概率区间实现对真实概率的覆盖；在气象条件e6下，训练样本中没有爬坡事件发生，这种情况下clt模型输出不爬坡概率为1而上/下爬坡概率为0，引发估计错误，而本发明提出的方法在这些条件下仍可以较好实现对光伏功率爬坡状态的概率估计，并能实现对真实概率的覆盖。

对于验证集中所有可能存在的气象状态组合的非精确估计结果进行统计，以整体分析clt模型与本发明方法在可靠性与敏锐性两方面的表现，两种方法在验证集中的对真实概率的覆盖率与平均概率区间宽度如表3所示。

表3验证集概率区间精度分析

为了进一步预测该光伏电站可能的功率爬坡情况，本发明在连续时间段内进行了非精确条件概率估计。未来5小时内，该光伏电站所在位置气象条件的变化情况如表a2所示，采用本发明方法预测未来时段光伏功率发生下爬坡事件的概率变化情况如图6所示。

表a2未来5小时气象条件的变化情况

由图6可见，在连续时段内该光伏电站的下爬坡概率不是固定值，其在不同预估时段的下爬坡概率区间不同体现了光伏电站功率稳定水平随气象条件变化而时变的特点。图中下爬坡概率区间的上界线为对光伏功率爬坡较为保守的估计，而下界线则对应较为乐观的估计。同时，利用经典贝叶斯网络精确单值条件概率估计的结果被包含在信度网络推理所得的概率区间内，证明了非精确概率对光伏功率爬坡事件具有更全面的描述特点，能够为电力系统运行决策提供更加全面的概率信息。

5结论

随着可再生能源的大量介入，配网调度运行人员需要得到更为全面的可再生能源的预测结果，依据其可能产生的影响进而制定有效的控制策略。在光伏功率爬坡事件样本有限的条件下，非精确概率方法可以充分考虑概率估计过程中可能出现的不确定性，所得结果为指定时刻的光伏功率爬坡事件发生的概率区间，覆盖了较为全面的预测信息。本发明提出的相对爬坡率有效剔除了规律性光伏功率变动的影响，运用信度网络学习算法构建了由气象因素引起的光伏功率爬坡事件与相关气象因素之间的映射关系，依据信度网络概率推来结合idm实现了对各爬坡状态发生的非精确概率推断。通过算例分析验证了方法的有效性，算例结果体现了因样本有限性导致的估计结果的不确定性，从而可为电力系统运行决策提供更为全面的光伏出力信息。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。