一种基于蒙特卡罗模拟法的GO法中的不确定性分析方法与流程

本发明属于乏燃料后处理设施的概率安全评价技术领域，具体涉及一种基于蒙特卡罗模拟法的go法中的不确定性分析方法。

背景技术：

go法是一种有效的系统可靠度分析方法。go法的基本原理是以操作符代表单元，以信号流代表单元之间的连接，将系统图转换成go图。go法的定量计算是从输入操作符开始，沿信号流序列，按操作符运算规则，逐步计算信号流的状态概率，直至代表系统的最终输出信号。go法在本世纪初不断发展，逐渐有了go法定量计算的新算法；并有了系统中共有信号的计算方法和传递规则，在多数情况下可以直接计算所有信号流的状态概率；进而发展了有共有信号的go法精确定量算法和可修系统中的go法算法，使go法的系统定量计算更为直接和简便。

go法也是概率安全评价(probabilisticsafetyassessment，简称psa)中一个重要的演绎类的系统分析方法。一般情况下，概率安全评级中所采用的各种模型(可靠性模型)中，参数不能够准确地得到，因此需要描述全部可能的输入输出结果，即进行不确定性分析。不确定性分析的目标分两类，在一般工程研究中，得到分布的方差即可；在psa中期望得到的结果显然不限于方差，而更期望得到完整的分布或足够多的、有代表性的离散点，以便给出各种置信区间。

不确定性分析的方法通常有矩法和积分法，后者包括解析积分法、数值积分法(离散函数分布法)、蒙特卡罗模拟法(montecarlomethod，简称mc)。解析积分法只有在函数形式简单、变量个数少且相互独立的情况下，操作比较现实可行；矩法和数值积分法也有类似的缺点。mc模拟法亦称统计模拟方法，利用随机数进行数值模拟，本质上属于积分法，靠大量随机事件概率累加，一般由试验模型(函数关系式)、抽样、对抽样结果进行统计分析三部分组成。

本发明中的不确定性分析专指部件的可靠性参数引起的不确定性分析，而不包括对构模精确程度的不确定性分析。目前，国外对go法的不确定性分析方面的研究工作较少，国内在此方面的工作基本属于空白，尚未见任何文献报道。

因此，有必要提供一种基于蒙特卡罗模拟法的go法中的不确定性分析方法以解决上述问题。

技术实现要素：

针对现有技术中存在的缺陷，本发明的目的是提供一种基于蒙特卡罗模拟法的go法中的不确定性分析方法，改善了概率安全评价中基于go法的不确定性分析，能为后续研究提供参考依据。

为达到以上目的，本发明采用的技术方案是：

一种基于蒙特卡罗模拟法的go法中的不确定性分析方法，所述方法包括：(1)部件的可靠性参数均取点估计值进行重要度分析；

(2)得出各部件抽样概率psample；

(3)对部件的可靠性参数进行抽样；

(4)不确定性分析结果可信评价。

进一步的，所述步骤(1)中所述点估计值获取方式包括：

直接采用，即原始点估计值；

数学期望，即通过部件可靠性参数的概率密度函数获取。

进一步的，所述步骤(1)中所述重要度为fv重要度和raw重要度。

进一步的，所述步骤(2)所述抽样概率psample计算公式为：

psample,i＝itype,i/itype,max

其中，psample,i为部件i的抽样概率；itype,i为部件i的type类型的重要度，type＝fv或raw；itype,max为所有部件type类型重要度的最大值。

进一步的，步骤(3)中包括：

当部件的可靠性参数为原始点估计值时，无需抽样；

当部件的可靠性参数为概率密度函数时，采用俄国轮盘赌的方法，比较psample,i与本次随机模拟开始时生成的随机数a的大小，若psample,i≥a，则进行抽样，否则不抽样，直接采用点估计值。

进一步的，在步骤(3)之后，步骤(4)之前还包括：

计算可靠性结果的相对误差r；

其中，r＝可靠性结果的方差/可靠性结果。

进一步的，步骤(4)具体包括：

根据可靠性结果的相对误差r评价不确定性分析结果的可信程度，当0.5<r<1时，为垃圾；当0.2<r≤0.5时，为不可信；当0.1<r≤0.2时，为可疑的；当0.05<r≤0.1时，为不可信；当r≤0.05时，为比较可信。

步骤(4)之后还包括步骤(5)：根据中心极限定律印证不确定性的分析结果：

当不确定性分析的结果的表达为：对数正态分布曲线(数据图形式)或者相应的对数正态分布参数(概率密度函数形式)时，则基本印证基于蒙特卡罗模拟法的go法中的不确定性分析是可靠的。

本发明的效果在于，本发明所述的方法，改善了概率安全评价中基于go法的不确定性分析，能为后续研究提供参考依据。

附图说明

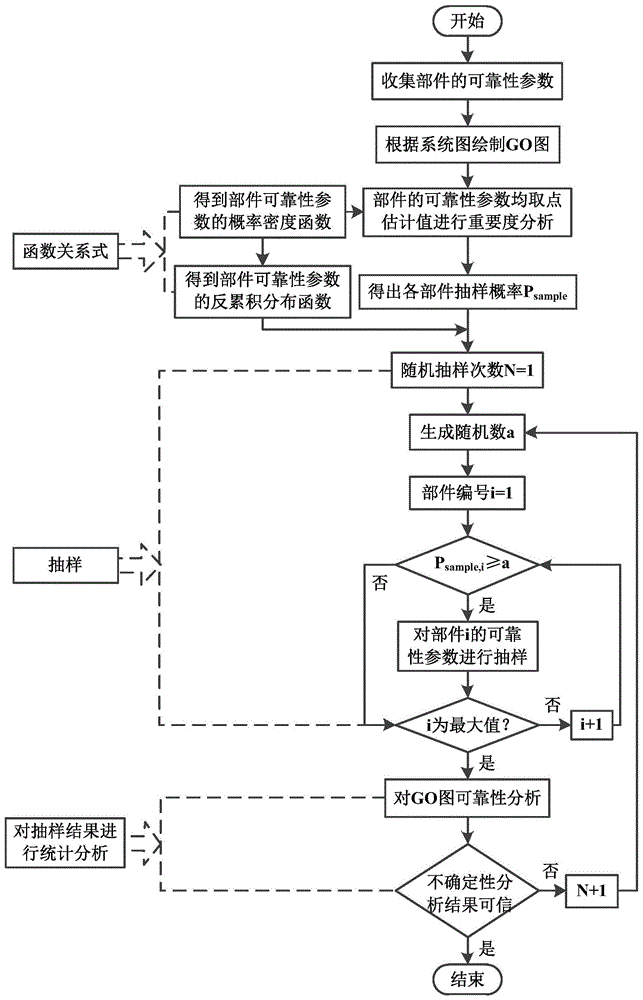
图1为基于mc模拟法的go法中的不确定性分析流程图；

图2为某供电系统的go图。

具体实施方式

为使本发明解决的技术问题、采用的技术方案和达到的技术效果更加清楚，下面将结合附图对本发明实施例的技术方案作进一步的详细描述。显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，均属于本发明保护的范围。

参阅图1，图1是本发明所述基于mc模拟法的go法中的不确定性分析流程图。

一种基于蒙特卡罗模拟法的go法中的不确定性分析方法，包括以下步骤：

步骤101：部件的可靠性参数均取点估计值进行重要度分析。

go法中部件的典型可靠性参数模型见表1。常见的可靠性参数有：频率事件、请求失效事件、不可修部件、非定期测试的可修部件以及定期测试的可修部件等等。

表1部件的典型可靠性参数模型

由于可靠性试验总是有损的并且收集到的数据是有限的，所以部件的可靠性参数一般都是缺乏的。在本发明中部件的可靠性参数取的点估计值有两种获取方式。

一是，直接采用原始点估计值。为了可靠性分析时计算简便，只考虑部件的可靠性参数为原始点估计值的情况。

二是，部件的可靠性参数(表1中第三列所示需要的参数)，可以由概率密度函数描述。比如，通常情况下，频率事件的发生次数服从泊松分布，请求失效型事件的需求失效次数服从二项分布，(不)可修部件的失效率λ服从γ分布。

当收集完部件的可靠性参数后，还需要根据系统图绘制go图。这种参数的不确定性将通过go图结构传播至最终的可靠性分析结果，例如图2所示的某供电系统的go图中，所有部件的可靠性参数的随机性都将影响供电输出的可靠性结果。

最后还需要得到各部件的重要度，主要是割集重要度(fussell-vesely，简称fv)和致险价值重要度(riskachievementworth，简称raw)，因为fv重要度和raw重要度是美国核管会(nrc)的psa导则中要求计算的重要度。

步骤102：得出各部件抽样概率psample。

抽样概率计算公式为：

psample,i＝itype,i/itype,max

其中，psample,i为部件i的抽样概率；itype,i为部件i的type类型的重要度，type＝fv或raw；itype,max为所有部件type类型重要度的最大值。

即根据各部件的重要度决定本次随机模拟是否需要抽样时，可根据这两个重要度中的任何一个。通过这样设置，可减少整体的计算工作量。

步骤103：对部件的可靠性参数进行抽样。

此处的抽样仅对可靠性参数来源于概率密度函数描述的部件而言，如果部件的可靠性参数仅以原始点估计值表示，则直接采用该值，无需抽样。具体的，根据psample,i决定本次随机模拟是否需要抽样，就是采用俄国轮盘赌的方法，比较psample,i与本次随机模拟开始时生成的随机数a的大小，若psample,i≥a，则进行抽样，否则不抽样，直接采用点估计值。

步骤104：不确定性分析结果可信评价。

在不确定性分析的同时，还需计算可靠性结果的相对误差r，r＝可靠性结果的方差/可靠性结果。根据r的范围可以知道不确定性分析结果的可信程度。具体的，当0.5<r<1时，为垃圾；当0.2<r≤0.5时，为不可信；当0.1<r≤0.2时，为可疑的；当0.05<r≤0.1时，为不可信；当r≤0.05时，为比较可信。

步骤104之后还包括步骤105：根据中心极限定律印证不确定性的分析结果：

由中心极限定理可知，大量独立、同分布的变量之积构成的新变量服从对数正态分布。因此，go图中最终输出事件发生概率的分布近似为对数正态分布。这可以用于印证mc模拟法对go图不确定性分析的结果。当不确定性分析的结果的表达为：对数正态分布曲线(数据图形式)或者相应的对数正态分布参数(概率密度函数形式)时，则基本印证基于蒙特卡罗模拟法的go法中的不确定性分析是可靠的。

区别于现有技术，本发明提供的一种基于蒙特卡罗模拟法的go法中的不确定性分析方法，改善了概率安全评价中基于go法的不确定性分析，能为后续研究提供参考依据。

本领域技术人员应该明白，本发明所述的方法并不限于具体实施方式中所述的实施例，上面的具体描述只是为了解释本发明的目的，并非用于限制本发明。本领域技术人员根据本发明的技术方案得出其他的实施方式，同样属于本发明的技术创新范围，本发明的保护范围由权利要求及其等同物限定。