一种陶瓷基复合材料在应力氧化环境下质量变化预测方法与流程

本发明属于材料质量变化预测
技术领域：
，特别涉及一种陶瓷基复合材料在应力氧化环境下质量变化预测方法。
背景技术：
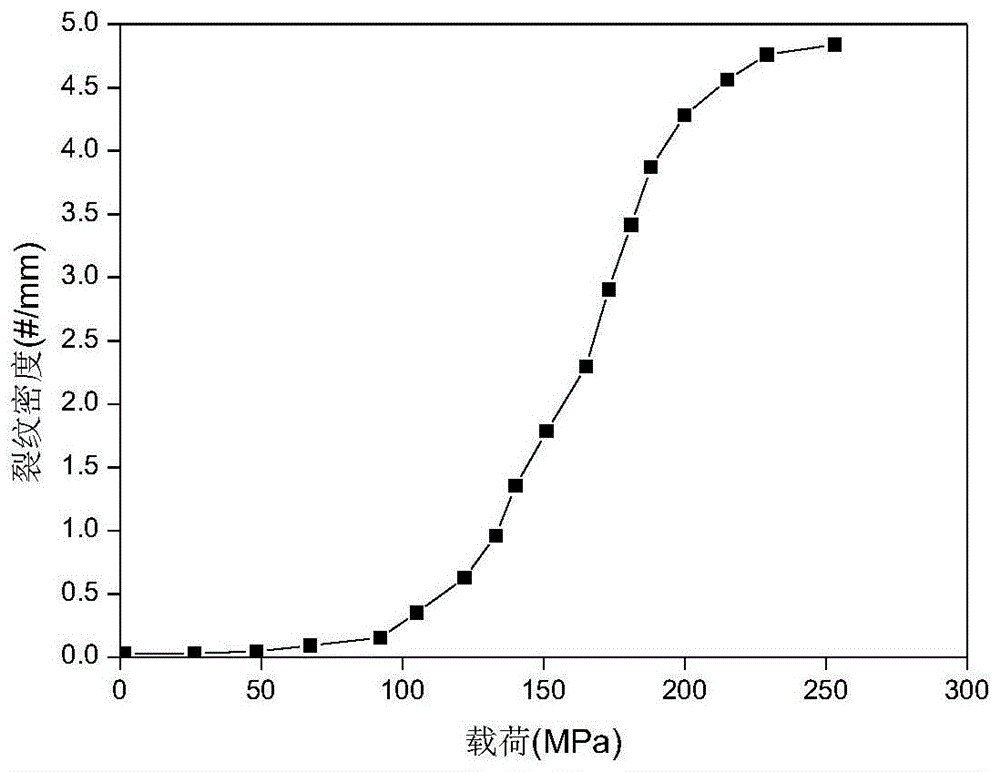
：碳化硅纤维增韧碳化硅陶瓷基复合材料(continuoussiliconcarbidefiberreinforcedsiliconcarbidecomposites，以下简称sic/sic)的耐高温、低密度、高比强、高比模等优异性能，使其成为航空航天领域不可替代的新型高温结构材料之一，广泛应用于航空、航天发动机热端部件、航空航天往返防热系统、高速刹车、燃气轮机热端部件、高温气体过滤和热交换器等。在sic/sic材料服役过程中，其不仅受到氧化性气体(如氧气)的高温腐蚀，同时要承受一定的载荷。在载荷的作用下，sic基体会出现许多裂纹，该裂纹会成为氧气进入材料内部的通道。在高温(>900℃)环境下,氧气的进入会造成界面、纤维、基体等组分材料的氧化损伤，进而引起材料的形貌及质量发生改变。快速有效的计算出单向sic/sic材料在应力氧化环境下的质量变化，能够为材料服役过程中的损伤检测、寿命评估提供重要的理论依据，并为材料在应力氧化环境下的可靠性设计提供必备的技术支持。目前，对于确定单向sic/sic材料在应力氧化环境下质量变化的技术主要有以下两种：专利cn105631148a“应力氧化环境下单向陶瓷基复合材料力学性能分析方法”基于裂纹个数、宽度随应力的变化规律和单向c/sic材料在400-900℃环境下的氧化机理，确定了应力氧化环境下单向c/sic材料的质量失重率。但是由于sic/sic材料和c/sic材料的氧化机理存在明显差异，该方法不能适用于sic/sic材料体系。另外，由于sic组分在900℃以上会开始发生氧化，该方法不适用于900℃以上的质量变化预测。因此，该方法无法准确预测单向sic/sic材料在高温(>900℃)环境下的质量变化。文献“oxidationmechanismsandkineticsof1d-sic/c/siccompositematerials:ii,modeling.j.am.cream.soc,1994.77(2):p.467-480.”公开了一种通过理论模拟单向sic/sic材料在无应力氧化环境下质量变化的测试方法，该方法基于热解碳与sic纤维、基体在高温(>900℃)环境下的化学反应方程，和传质学的二元扩散理论，对氧化不同时间后的材料形貌和质量变化进行了预测。但该方法仅适用于无应力氧化环境下的质量变化预测，不能用于应力氧化环境下sic/sic材料的质量变化预测。此外，该方法只考虑垂直纤维方向横截面处的氧化，不考虑基体裂纹的存在对组分氧化的影响。因此，该方法无法准确预测单向sic/sic材料在应力氧化环境下的质量变化。综上所述，有必要提供一种简单有效、能够准确预测单向sic/sic材料在应力氧化环境下的质量变化预测方法。技术实现要素：本发明针对上述现有技术的不足，提供了一种陶瓷基复合材料在应力氧化环境下质量变化预测方法，以解决现有技术中对单向sic/sic材料质量变化的分析未考虑应力和高温(>900℃)氧化的共同作用的问题。为实现上述目的，本发明采用的技术方案为：一种陶瓷基复合材料在应力氧化环境下质量变化预测方法，包括以下步骤：步骤一：确定材料在应力和高温作用下的基体裂纹数量的变化规律；步骤二：确定材料在应力和高温作用下的基体裂纹宽度的变化规律；步骤三：基于传质学的二元扩散理论，确定氧气在裂纹通道内的扩散系数；步骤四：基于c界面、sic纤维、基体在高温氧气环境下的氧化机理，分别确定各组分的氧化速率；步骤五：基于反应前后物质变化，确定sic纤维、基体反应前后的体积变化；步骤六：基于步骤三、四的结果，确定单向sic/sic材料在应力、高温氧化环境下的氧化动力学模型；步骤七：基于步骤二、六的结果，确定裂纹扩散阶段和界面层扩展阶段的氧化动力学模型，进而确定氧化层变化规律和界面消耗规律；步骤八：基于步骤一、五、七的结果，确定应力、高温环境下的单向sic/sic材料的质量变化规律。进一步的，所述步骤一包括以下步骤：根据蒙特卡罗法，假设基体的失效概率服从泊松分布，在单轴拉伸应力作用下，长度ls的复合材料上产生n条裂纹的概率p为：p(ξ＝σ,η＝ls)＝1-exp{-m(a)},n(a)≥1式中，ξ为应力值，η为基体长度值，σ为施加的轴向应力，ls为复合材料的基体长度，m(a)为泊松参数，n(a)表征应力作用下产生的裂纹条数，m为威布尔参数，也叫形状参数；σr、δr分别为特征应力和对应的特征界面滑移长度，σth表征复合材料中的热残余应力，σmc为基体的初始开裂应力；为消除基体总长度的影响，选用裂纹密度ρcrack作为轴向应力的函数对基体表面的裂纹进行表征：式中：n为裂纹数目，由蒙特卡洛计算方法得到。进一步的，所述步骤二包括以下步骤：基体在应力和高温条件下分别受到轴向拉应力σm和热残余应力σth：式中，em、ef分别为基体和纤维的弹性模量，αm、αf分别为基体和纤维的热膨胀系数，vm、vf分别为基体和纤维的体积分数，δt表征制备温度和当前温度的温差；在不考虑外加应力时，得到基体裂纹宽度与温度的关系为：式中，t为环境温度，t0为材料的制备温度，e为裂纹在温度t下的宽度，e0为常温时的裂纹宽度；得到基体裂纹宽度与热残余应力的关系：在考虑外加轴向应力时，以总应力项σm+σth代替上式热残余应力，得到裂纹宽度与应力、温度的关系：其中：δt表征制备温度和当前温度的温差。进一步的，所述步骤三包括以下步骤：根据传质学的二元扩散理论，在假设氧化气体产物为co的前提下，得到氧气在裂纹中的扩散通量为：式中，y为沿裂纹深度方向的坐标值，nco表示氧气o2和一氧化碳co相对于固定坐标y轴的扩散通量，c0为该体系中总的物质的量浓度；表示氧气在裂纹通道中的扩散系数；表示o2的摩尔分数，其物理意义为o2的物质的量浓度和总物质的量浓度之比，即由于基体裂纹的尺寸与分子的大小关系，氧气在裂纹通道内的扩散属于过渡扩散，即包括分子扩散和knudsen扩散，得到扩散系数的表达式：式中，dab为分子扩散系数，dka为o2在特征尺寸为e的缺陷中扩散的knudsen扩散系数，e由步骤二确定，其计算公式如下给出：式中，pair为环境压强，(σv)co分别为o2、co的扩散体积，为混合气体的摩尔质量，mco分别为o2、co的摩尔质量，r为理想气体常数，π为圆周率。进一步的，所述步骤四包括以下步骤：根据c的氧化机理，得到c界面的氧化速率rc：式中，kc为c的反应速率常数，k0为表征反应速率的常数，ec为该反应的c的活化能，为o2的物质的量浓度；根据sic的氧化机理，由deal-grove模型和亨利定律，得到sic基体、纤维的氧化速率：式中，k为亨利常数，是仅为温度相关的函数，为外界氧分压，n1则是指形成单位体积sio2所需要的氧化剂分子数；sic基体、纤维的氧化速率b的值常由试验确定，根据其随温度的变化规律，得到b随氧气浓度变化的修正公式：式中，b*和c*分别表示100kpa纯氧环境下的sic基体、纤维的氧化速率和氧气浓度，p为反应指数。进一步的，所述步骤五包括以下步骤：根据sic反应前后的质量变化和密度关系，得到sic反应前后的体积变化：式中，νf、νm分别为纤维和基体的体积变化比例，为生成的sio2的体积，vsic为发生反应的sic的体积，msic分别为sio2、sic的摩尔质量，ρsic分别为sio2、sic的密度。进一步的，所述步骤六包括以下步骤：根据质量守恒定律，得到扩散通量与氧气消耗量的关系：式中，s为气体流通横截面积，s＝l*e，l为裂纹长度，e由步骤二确定；由步骤三确定，为单位长度内y处消耗氧气的量；由步骤四，得到氧化层sio2的厚度与氧气浓度和环境温度的关系式：式中，为y处生成的sio2厚度；结合sic氧化方程式的比例关系，得到位置y处每秒消耗氧气的量：式中，g为产生1molsio2所需氧气的物质的量；进而得到材料内部任意时间下的氧化动力学方程：式中，α为裂纹通道内的co和o2的摩尔通量的比例关系。进一步的，所述步骤七包括以下步骤：结合基体环形裂纹扩散阶段和界面消退扩展两个阶段，根据步骤六的结果，得到各自的氧化动力学方程及边界条件：式中，rt为基体表面到纤维圆心的距离，hm(y,t)为y处t时刻的sio2层相对于壁面突出的厚度，d为裂纹宽度e的一半，d1表示基体环形裂纹扩散阶段氧气在裂纹通道中的扩散系数，gm为sic基体产生1molsio2所需氧气的物质的量,bm*为100kpa纯氧环境下的sic基体的氧化速率，pm为基体反应级数，表示基体环形裂纹扩散阶段基体处生成的sio2厚度；以及界面层扩展阶段的氧化动力学方程：式中，z为沿界面层方向的坐标值，d2表示界面层扩展阶段氧气在裂纹通道中的扩散系数，rm为基体与界面交界处到纤维圆心的距离，rf为纤维的半径，其随时间而变化；gf为sic纤维产生1molsio2所需氧气的物质的量,bf*为100kpa纯氧环境下的sic纤维的氧化速率，pf为纤维反应级数，表示界面消退扩展阶段基体处生成的sio2厚度,界面消退扩展阶段纤维处生成的sio2厚度；且有表示界面消退扩展阶段起始位置处基体生成的sio2厚度,，表示基体环形裂纹扩散阶段终了位置处纤维生成的sio2厚度；结合裂纹顶端(y＝0)、界面氧化处(z＝lr)、裂纹底端(y＝l,z＝0)的边界条件其中：l为裂纹深度，lr为任一时刻下c界面氧化长度；式中，pc为c相反应指数；基于四阶龙格库塔法对两阶段的氧化动力学模型进行求解，得到任一时刻下c界面氧化长度lr、裂纹通道内任一位置的sio2厚度以及界面通道任一位置的sio2厚度进一步的，所述步骤八包括以下步骤：结合步骤一得到的裂纹数目，步骤三得到的体积变化，和步骤六得到的基体、纤维氧化层厚度变化和界面的消耗情况，得到单向sic/sic复合材料的质量变化规律：mtotal＝vfρf+vmρm+vcρc式中，δm为材料总的质量变化，mtotal为材料初始质量，δmsurf为模型表面sic基体的氧化增重，δm1为c界面的氧化失重，δm2为模型内部基体的氧化增重，δm3为纤维的氧化增重，模型内部基体上氧化层的体积，纤维表面生成的氧化层的体积，表示模型表面基体上氧化层的体积，ρf、ρm、ρc分别表示纤维、基体、界面的密度。与现有技术相比，本发明具有以下有益效果：(1)本发明方法考虑了应力与高温氧化对单向sic/sic复合材料的氧化机理的共同作用，为陶瓷基复合材料在应力氧化环境(>900℃)下的力学性能分析提供了相关理论支持；(2)本发明方法考虑了氧气从裂纹通道进入向内扩散，以及沿界面通道扩散的两个阶段，可以准确预测氧化一定时间后材料的形貌变化和质量变化；(3)采用本发明方法预测的单向sic/sic复合材料在应力氧化环境(>900℃)下质量变化值与试验值吻合度较高；(4)计算过程简洁有效，省去了实验方法的时间和人力成本。附图说明图1是基体裂纹密度随外加载荷的变化曲线；图2是基体裂纹宽度随温度和应力的变化曲线；图3是单向sic/sic复合材料内部氧化过程示意图图4(a)是单向sic/sic复合材料模型；图4(b)是sic/sic复合材料氧化模型侧视图；图5是材料裂纹处几何形貌；图6是材料界面散通道处几何形貌；图7(a)是900-1200℃时，80mpa加载条件下，单向sic/sic复合材料裂纹顶端处基体上氧化层厚度随时间和温度的变化曲线；图7(b)是900-1200℃时，200mpa加载条件下，单向sic/sic复合材料裂纹顶端处基体上氧化层厚度随时间和温度的变化曲线；图8(a)是900-1200℃时，80mpa加载条件下，单向sic/sic复合材料界面处纤维上氧化层厚度随时间和温度的变化曲线；图8(b)是900-1200℃时，200mpa加载条件下，单向sic/sic复合材料界面处纤维上氧化层厚度随时间和温度的变化曲线；图9(a)是900-1200℃时，80mpa加载条件下，单向sic/sic复合材料界面消耗长度随时间和温度的变化曲线；图9(b)是900-1200℃时，200mpa加载条件下，单向sic/sic复合材料界面消耗长度随时间和温度的变化曲线；图10是900℃时，单向sic/sic复合材料界面消耗长度随时间和加载应力的变化曲线；图11(a)是900-1200℃时，80mpa加载条件下，单向sic/sic复合材料质量变化率随时间和温度的变化曲线；图11(b)是900-1200℃时，200mpa加载条件下，单向sic/sic复合材料质量变化率随时间和温度的变化曲线；图12是900℃时，单向sic/sic复合材料质量变化率随时间和加载应力的变化曲线；图13是1200℃时，单向sic/sic质量变化率模拟值与试验值的数据对比。具体实施方式下面结合实施例对本发明作更进一步的说明。对本发明方法预测单向sic/sic复合材料在应力氧化环境(900-1200℃)下的质量变化做进一步说明：具体实施步骤中，环境为纯氧环境，sic纤维采用日本碳公司的nicalon系列，其材料参数如表1所示：表1nicalon系列纤维参数本实施例中选用nicalon型号(表1第一列)的sic纤维，考虑其元素组成，表示为sixcyoz(x：y：z＝1；1.35；0.375)。步骤一：确定材料在应力和高温作用下的基体裂纹数量的变化规律；根据蒙特卡罗法，假设基体的失效概率服从泊松分布，在单轴拉伸应力σ的作用下，长度ls的复合材料上产生n条裂纹的概率p为：p(ξ＝σ,η＝ls)＝1-exp{-m(a)}，n(a)≥1(1)式(1)中，ξ为应力值，η为基体长度值，ls为复合材料的基体长度，σ为外加轴向应力(取值80～200mpa)，m(a)为泊松参数，n(a)表示该应力作用下产生的裂纹条数。式(2)为泊松参数的表达式，m为威布尔参数，也叫形状参数(取值为3.5～4，本例中取4)；σr、δr分别为特征应力和对应的特征界面滑移长度，σth表征复合材料中的热残余应力，σmc为基体的初始开裂应力。为消除基体总长度的影响，选用裂纹密度ρcrack作为轴向应力的函数对基体表面的裂纹进行表征：式(3)中n为裂纹数目，由蒙特卡洛计算方法得到。得到在外加轴向应力σ下的裂纹密度随拉伸应力变化曲线，如附图1所示。步骤二：确定材料在应力和高温作用下的基体裂纹宽度的变化规律；在外加轴向应力σ(80-200mpa)和高温(1173-1473k)的作用下，sic基体分别受到轴向拉应力σm和热残余应力σth：式中，em、ef分别为基体和纤维的弹性模量，αm、αf分别为基体和纤维的热膨胀系数，vm、vf分别为基体和纤维的体积分数，δt表征制备温度和当前温度的温差。在不考虑外加应力时，得到基体裂纹宽度与温度的关系为：式中，t为环境温度(取开氏温度，t＝1173-1473k)，t0为材料的制备温度，e为裂纹在温度t下的宽度，e0为常温时的裂纹宽度。得到基体裂纹宽度与热残余应力的关系：在考虑外加轴向应力时，以总应力项σm+σth代替上式热残余应力，得到裂纹宽度与应力、温度的关系：裂纹宽度相关参数如表2所示，得到的基体裂纹宽度随温度和应力变化曲线如图2所示。表2裂纹宽度相关参数步骤三：基于传质学的二元扩散理论，确定氧气在裂纹通道内的扩散系数；根据传质学的二元扩散理论，在假设氧化气体产物为co的前提下，得到氧气在裂纹中的扩散通量为：式(9)中，y为沿裂纹深度方向的坐标值，表示氧气在裂纹通道中的扩散系数，nco表示氧气(o2)和一氧化碳(co)相对于固定坐标y轴的扩散通量；c0为该体系中总的物质的量浓度；表示o2的摩尔分数，其物理意义为o2的物质的量浓度和总物质的量浓度之比由于基体裂纹的尺寸与分子的大小关系，氧气在裂纹通道内的扩散属于过渡扩散，即包括分子扩散和knudsen扩散，得到扩散系数的表达式：式中，dab为分子扩散系数，dka为o2在特征尺寸为e的缺陷中扩散的knudsen扩散系数，e由步骤二确定。其计算公式如下给出：式中，pair为环境压强(pair＝100kpa)，(σv)co分别为o2、co的扩散体积((σv)o2＝16.6、(σv)co＝18.9)，m为混合气体的摩尔质量，mco分别为o2、co的摩尔质量(mco＝28[g/mol])，r为理想气体常数(r＝8.314j/[mol·k])，π为圆周率(π＝3.14)。步骤四：基于c界面、sic纤维、基体在高温氧气环境下的氧化机理，分别确定各组分的氧化速率；由于氧气在裂纹中的扩散速率小于其与c的反应速率，因此c界面的氧化受氧气扩散控制，产物以co为主。c界面的反应速率为：式(14)中，kc为c的反应速率常数，k0为c界面的反应速率常数(k0＝0.49)，ec为该反应的活化能(ec＝104433[j/mol])，为反应位置处的氧气浓度。在标准大气压下，sic发生被动氧化，产物为co和sio2，根据deal-grove模型和亨利定律，sic基体、纤维的氧化速率为：b值由试验测得，根据试验数据拟合得到修正关系，将上式改写为：式(16)中，b*和c*分别表示100kpa纯氧环境下的sic基体、纤维的氧化速率和氧气浓度(c*＝45[mol/m3])，p为反应指数。其相关参数如表3所示，其中下标m代指基体，f代指纤维。表3nicalon纤维和sic基体高温氧化参数步骤五：基于反应前后物质变化，确定sic纤维、基体反应前后的体积变化；sic材料因氧化而在其表面生成氧化层，会导致材料的体积发生变化，得到其基体、纤维的体积变化关系：式中，为生成的sio2的体积，vsic、分别为反应消耗的基体和纤维的体积，为sio2的摩尔质量，msic、为基体和纤维的摩尔质量，为sio2的密度，ρsic、为基体和纤维的密度。材料组分的基本参数如表4所示：表4材料组分基本参数步骤六：基于步骤三、四的结果，确定单向sic/sic材料在应力、高温氧化环境下的氧化动力学模型；根据质量守恒定律，得到扩散通量与氧气消耗量的关系：其中s为气体流通横截面积，s＝l*e，l为裂纹长度，e为裂纹宽度，由步骤二确定；其中由步骤三确定，为单位长度内y处消耗氧气的量由步骤四，得到氧化层sio2的厚度与氧气浓度和环境温度的关系式：式(19)中，为y处生成的sio2厚度。结合sic氧化方程式的比例关系，得到位置y处每秒消耗氧气的量：式(20)中，g为产生1molsio2所需氧气的物质的量(g＝1.5)。进而得到材料内部任意时间下的氧化动力学方程：式(21)中，c0为该体系中总的物质的量浓度，此处为纯氧环境，表示初始时的氧气浓度(c0＝p/rt＝101×103/8.314/t[mol/m3])，式中，α为裂纹通道内的co和o2的摩尔通量的比例关系。(α＝2)。单向sic/sic复合材料在高温环境下的氧化过程如图3所示，氧化模型如图4所示。步骤七：基于步骤二、六的结果，确定裂纹扩散阶段和界面层扩展阶段的氧化动力学模型，进而确定氧化层变化规律和界面消耗规律；根据步骤六得到的氧气在裂纹通道内的氧化动力学方程，结合基体环形裂纹扩散阶段和界面消退扩展阶段，得到各自的氧化动力学方程及边界条件：裂纹扩散阶段的氧化动力学方程为：式(22)中，2d为步骤四得到的裂纹宽度e，rt为基体表面到纤维圆心的距离，hm为y处sio2层相对于壁面突出的厚度，d1表示基体环形裂纹扩散阶段氧气在裂纹通道中的扩散系数，由步骤三求得。gm为sic基体产生1molsio2所需氧气的物质的量,bm*为100kpa纯氧环境下的sic基体的氧化速率,pm为基体反应级数，表示基体环形裂纹扩散阶段基体处生成的sio2厚度。该阶段的氧化几何形貌如图5所示。界面层扩展阶段的氧化动力学方程为：式(23)中，rm为基体与界面交界处到纤维圆心的距离，rf为纤维的半径，其随时间而变化，d2表示界面层扩展阶段氧气在裂纹通道中的扩散系数，由步骤三求得。gf为纤维产生1molsio2所需氧气的物质的量,bf*为100kpa纯氧环境下的纤维的氧化速率,pf为纤维反应级数，表示界面消退扩展阶段基体处生成的sio2厚度,界面消退扩展阶段纤维处生成的sio2厚度。且有该阶段的氧化几何形貌如图6所示。裂纹顶端(y＝0)、界面氧化处(z＝lr)、裂纹底端(y＝l,z＝0)的边界条件(l为裂纹深度,lr为任一时刻下c界面氧化长度)：式(25)中，pc为c相反应指数(pc＝0.3)。与两阶段氧化动力学方程相关的初始几何参数如表5所示。表5模型初始几何参数参数数值纤维初始半径：rf0[μm]7基体表面到纤维圆心的距离：rt[μm]10基体与界面交界处到纤维圆心的初始距离：rm0[μm]7.1基于四阶龙格库塔法对两阶段的氧化动力学方程进行求解，得到任一时刻下裂纹顶端处基体上的sio2厚度其结果如图7所示。由图可知：随氧化时间的增加，基体上的氧化层厚度呈抛物线规律增长，且温度越高，增长速率越快，氧化终止时间越短，终止时的氧化层厚度也越小。其原因在于sic与o2的反应速率随温度升高而增加，而裂纹宽度随温度升高而减小，裂纹闭合后氧化终止。此外，应力对氧化层厚度的影响也是由于对裂纹宽度的作用产生，而不影响氧化速率，故200mpa下的氧化终止时间比80mpa下的更长。同时得到任一时刻下界面通道内纤维上的sio2厚度其结果如图8所示。由图可知：在相同的外加载荷(80-200mpa)、相同温度(900-1200℃)下，纤维上的氧化层厚度随时间、温度的变化规律与裂纹顶端处基体上的氧化层厚度变化规律一致，且氧化终止时间相当。其原因在于在此条件下，两者的氧化终止时刻都发生在裂纹处的通道闭合时。同时得到任一时刻下c界面氧化长度(lr)，其结果如图9所示。以及在不同应力加载下，900℃时界面消耗长度的变化曲线，如图10所示。由图9可知：随氧化时间的增加，c界面的消耗长度增加，氧化速率下降程度比基体和纤维的氧化更快，其原因在于氧气抵达界面反应处的难度随时间而增加。此外，温度越高，氧化速率下降越快，其原因也是由于sio2氧化层的加速增加导致氧气扩散更有难度。由图10可知：载荷的增加(80-200mpa)仅增加氧化终止时间，对氧化速率等均无影响，其原因也可由载荷仅对裂纹产生影响进行解释。步骤八：基于步骤一、五、七的结果，确定应力、高温环境下的单向sic/sic材料的质量变化规律；结合步骤一得到的裂纹数目，步骤三得到的体积变化，和步骤六得到的氧化层厚度变化与c界面氧化长度变化，确定单向sic/sic复合材料的质量变化规律：上述式中，δm为材料总的质量变化，mtotal为材料初始质量，δmsurf为模型表面sic基体的氧化增重，δm1为c界面的氧化失重，δm2为模型内部基体的氧化增重，δm3为纤维的氧化增重，模型内部基体上氧化层的体积，纤维表面生成的氧化层的体积，表示模型表面基体上氧化层的体积。单向sic/sic复合材料的质量变化率的变化关系如图11所示。由图可知，随氧化时间的增加，sic/sic材料的质量变化率先降低后升高，且随温度升高，曲线拐点出现的时间越早。拐点的出现是裂纹闭合的结果，拐点之前c界面对的消耗导致质量下降占主导，裂纹闭合之后，仅有基体的氧化增重。900℃时单向sic/sic复合材料的质量变化率在不同外加应力的情况下随时间的变化关系如图12所示。由图可知，随外加应力的增加，拐点出现的越晚。这是由于外加应力增加导致的裂纹宽度增大和裂纹密度增大，使得封填裂纹所需时间增加的缘故。在氧化发生的前300min内，sic/sic复合材料的质量变化率一直小于0，这表明这段时间内，基体和纤维的氧化增重仍不足以抵消c界面的消耗。比较本发明方法得到的1200℃时的质量变化率与试验值数据，如图13所示，发现本发明方法得到的预测值与试验结果一致性较高，说明该方法具有合理性。以上所述仅是本发明的优选实施方式，应当指出：对于本
技术领域：
的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。当前第1页12