一种旋转环状周期结构的弹性振动计算方法与流程

本发明涉及弹性振动计算领域，尤其涉及一种受三轴空间旋转运动作用的环状周期结构的弹性振动计算方法。

背景技术：

环状周期结构广泛应用于各工程领域，例如：行星齿轮传动的齿圈、旋转电机的环形定转子、叶盘结构、滚动轴承的内外圈以及陀螺仪等微器件中的环形构件。在工程实际中，该类结构将出现显著的振动、噪声以及稳定性问题。由于现有动力稳定性分析技术的适用范围的有限性，特别需要提出一种既考虑复杂的实际工况，又高效、准确的分析技术。

文献(esmaeilim,duralim,jalilin.ringmicrogyroscopemodelingandperformanceevaluation.journalofvibrationandcontrol,2006,12(5):537-553)以陀螺仪为研究对象，建立了复杂的动力学模型，研究了基础运动对动力学行为的影响机理。但是，该文献忽略了基础运动对动力稳定性的影响。

文献(yoonsw,leesw,najafik.vibrationsensitivityanalysisofmemsvibratoryringgyroscopes.sensorsandactuators:physical,2011,171:163-177)采用拉格朗日方法建立了计入面内弯曲振动和刚体振动的多维动力学模型，分析了振动对输出特性的影响，还探讨了制造误差和对称性与振动模态的关系及其对陀螺仪误差的影响。但是，该文献仅研究了基础的定轴转动情形。

此外，现有技术还通常采用数值方法预测动力稳定性，该方法的计算效率较低，且不能揭示普适规律。

技术实现要素：

本发明提供了一种旋转环状周期结构的弹性振动计算方法，本发明解决了现有弹性振动分析技术仅限于静止或定轴转动结构的不足，从而使得计算结果更好地满足工程需求，详见下文描述：

一种旋转环状周期结构的弹性振动计算方法，所述方法包括以下步骤：

在随动坐标系下建立动力学模型；求解光滑圆环的特征值；

根据摄动法求解环状周期结构的一阶摄动特征值；

借助三角函数的运算性质，判断振动波数与离散支撑个数之间的组合关系，然后分类计算环状周期结构的特征值；

根据得到的环状周期结构的特征值判断模态特性和动力稳定性；

求解环状周期结构的耦合系数，揭示组合的不稳定规律。

其中，所述动力学模型具体为：

式中，g⁽⁰⁾为陀螺算子，d⁽⁰⁾为向心刚度算子，k⁽⁰⁾和k⁽¹⁾表示由圆环弯曲及支撑产生的刚度算子，ε为无量纲小参数。

进一步地，所述光滑圆环的特征值具体为：

式中，ωvx、ωvy、ωvz分别为圆环绕x、y和z轴转动的无量纲转速，ku和kv分别为切向和径向刚度；n为波数。

其中，所述一阶摄动特征值具体为：

式中，bm和cm分别为：

bm＝2rn0-in4ωvz

式中，ks为倾斜支撑的刚度；β为倾斜支撑与环状周期结构径向的夹角；an为幅值，“～”表示共轭；n为离散倾斜支撑的个数。

进一步地，所述借助三角函数的运算性质，判断振动波数与离散支撑个数之间的组合关系，然后分类计算环状周期结构的特征值具体为：

当rn0为纯虚数和不为纯虚数时，分别获取后行波余弦、后行波正弦的特征值、前行波余弦、前行波正弦的特征值。

本发明提供的技术方案的有益效果是：

1、本发明首先借助随动坐标系建立动力学方程，然后通过求解光滑圆环的特征值，根据摄动方法求出相应周期结构的特征值，并根据周期结构的特征值预测固有频率分裂和稳定性规律；并且根据耦合系数，揭示波数、转速对组合不稳定的影响规律；

2、本发明采用解析法给出了环状周期结构的特征值，根据特征值判断系统的固有频率分裂规律和动力稳定性；

3、与现有技术相比，本发明具有高效、准确和普适特征，根据该技术可揭示参数与模态特性及动力稳定性之间的关系，实现在设计阶段预估振动状况，尤其是确定各阶振动的不稳定域，从而指导旋转对称机械的动力学设计，提高运行稳定性和可靠性。

附图说明

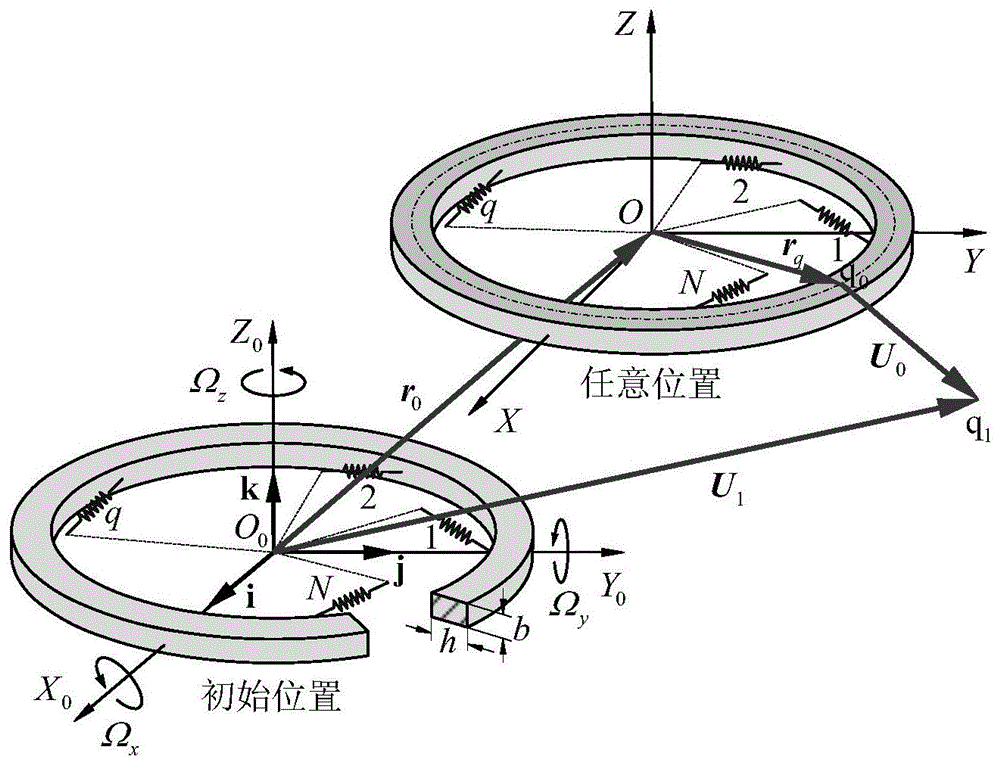
图1为本发明提供的旋转环状周期结构及坐标系的示意图；

图2为根据本发明提供的技术获得的光滑圆环不稳定域随转速和支撑刚度的变化规律的示意图；

图3为当参数满足2n/n是整数时，根据本发明提供的技术获得的特征值实虚部随转速的变化规律的示意图；

图4为当参数满足2n/n不是整数时，根据本发明提供的技术获得的特征值实虚部随转速的变化规律的示意图；

图5为当参数n是零时，根据本发明提供的技术获得的特征值实虚部随转速的变化规律的示意图；

图6为根据本发明提供的技术获得的耦合系数随波数的变化规律的示意图；

图7为当参数满足(n+m)/n≠整数且(n-m)/n＝整数时，根据本发明提供的技术获得的耦合系数随转速的变化规律的示意图；

图8为当参数满足(n+m)/n＝整数且(n-m)/n≠整数时，根据本发明提供的技术获得的耦合系数随转速的变化规律的示意图；

图9为当参数满足(n+m)/n＝整数且(n-m)/n＝整数时，根据本发明提供的技术获得的耦合系数随转速的变化规律的示意图。

其中，图中btwc表示后行波余弦，btws表示后行波正弦，ftwc表示前行波余弦，ftws前行波正弦。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面对本发明实施方式作进一步地详细描述。

本发明实施例提出了一种适用性较强的专门针对环状周期结构的弹性振动分析技术，本发明实施例首先借助随动坐标系建立环状周期结构的动力学模型，然后采用摄动法计算环状周期结构的特征值，从而预测模态特性和动力稳定性。

本发明实施例可适用于行星齿轮传动的齿圈、旋转电机的定转子、滚动轴承的内外圈、以及微器件中的环形构件等典型空间运动旋转对称构件的弹性振动特性的预测。

本发明实施例的技术方案如下：一种受空间多个旋转作用的环状周期结构的弹性振动分析技术，所述技术同时考虑了圆环的基础运动、切向(u)及径向(v)弹性振动产生的动力稳定性。

所述旋转环状周期结构由薄圆环、离散倾斜支撑和连续径向及切向支撑组成；所述结构受三个沿正交方向的旋转作用；所述弹性振动分析技术的基本特征在于：采用随动坐标系实现空间运动环状周期结构的动力稳定性解析预测，具体步骤为：

(a1)借助随动坐标系，根据hamilton原理建立所述环状周期结构的动力学模型：

式中，g⁽⁰⁾为陀螺算子，d⁽⁰⁾为向心刚度算子，k⁽⁰⁾和k⁽¹⁾表示由圆环弯曲及支撑产生的刚度算子，ε为无量纲小参数。

图1为环状周期结构及坐标系，其中x0y0z0为惯性坐标系，xyz为随动坐标系，二者的三个坐标轴分别平行，i、j和k均为单位矢量。随动坐标系以角速度ω绕惯性系旋转,ωvx、ωvy、ωvz分别为圆环绕x、y和z轴转动的无量纲转速，θ为位置角，δ(θ-θq)为狄拉克函数，δ′(θ-θq)为狄拉克函数的导数。o0和o表示几何形心位置。该结构的径向厚度、轴向高度、密度、杨氏模量、截面惯性矩和中性圆半径分别依次用h、b、ρ、e、i和r表示。

该环状周期结构内侧设置由n个离散的倾斜支撑，假定各倾斜支撑的刚度均为ks，各倾斜支撑与该环状周期结构径向的夹角均为β。同时假定第一个倾斜支撑位于极轴，则θq(θq＝2π(q-1)/n，q＝1，2，3，…，n)为第q个支撑的位置角。环状周期结构的外侧设置均匀支撑(未示出)，其切向和径向刚度分别为ku和kv。i(i＝bh³/12)为圆环的截面惯性矩。

(a2)求解光滑圆环的特征值，假设中间变量：

式中，为虚数单位，rn0为光滑圆环固有频率，an为幅值，“～”表示共轭，n为波数。定义内积如下：

然后将该假设公式(6)和公式(7)代入步骤(a1)的动力学方程中，并依据公式(8)与e^inθ作内积，可得圆环的固有频率如下：

(a3)根据摄动法求解环状周期结构的一阶摄动特征值，为此假设：

rn＝rn0+εrn1(10)

式中，rn1为一阶摄动。将该假设代入步骤(a1)的动力学方程中，然后与e^inθ作内积，化简可得环状周期结构的一阶摄动特征值：

式中，bm和cm分别为：

bm＝2rn0-in4ωvz(13)

(a4)根据三角函数的运算特性，有：

据此可分析波数及支撑个数对特征值的影响，揭示参数与模态特性及动力稳定性的映射关系。

(a5)求解环状周期结构的特征值，将步骤(a2、a3)中的rn0及rn1代入rn＝rn0+εrn1，运用(a4)的三角函数性质，进行分类讨论，得出固有频率分裂及稳定性规律，具体包括：

(a)当rn0为纯虚数时，有：

假设中间变量：

根据传播方向和振动模式可得两种情形，即：后行波(im(rn0)＝2nωvz+an)和前行波(im(rn0)＝2nωvz-an)。已知响应的余弦振幅为而正弦振幅为

后行波余弦的特征值为：

后行波正弦的特征值为：

前行波余弦的特征值为：

前行波正弦的特征值为：

(b)当rn0不为纯虚数时，有：

假设：

根据传播方向和振动模式，可分为后行(re(rn0)＝2nωvz+bni)和前行(re(rn0)＝2nωvz-bni)的典型情况。余弦和正弦振幅分别为：和

后行波余弦特征值为：

后行波正弦特征值为：

前行波余弦的特征值为：

前行波正弦的特征值为：

(a6)求解环状周期结构的耦合系数，得出组合不稳定规律，为此假设中间变量：

un＝un0+εun1(28)

式中，un0为光滑圆环的切向变形量，un1为环状周期结构的一阶摄动变形量，cnm为耦合系数，m为波数，将该假设代入步骤(a1)的动力学方程中，然后与e^imθ作内积，化简可得耦合系数：

式中，

ct＝2πam(fn+fmn+fm)(33)

为了更好地分析环状周期结构的组合不稳定规律，根据参数的变化，对耦合系数进行分类。cnmas、cnmac分别表示当参数满足条件(a)时，正、余弦模态的耦合系数。同理，cnmbs,c、cnmcs,c和cnmds,c表示当参数分别满足条件(b)、(c)和(d)时，正、余弦模态的耦合系数。

(a)当(n+m)/n≠整数及(n-m)/n≠整数时，有：

cnmac,s＝0(37)

(b)当(n+m)/n≠整数及(n-m)/n＝整数时，有：

(c)当(n+m)/n＝整数及(n-m)/n≠整数时，有：

(d)当(n+m)/n＝整数及(n-m)/n＝整数时，有：

基于所述式(1)的数学模型可分析其它旋转对称结构的动力学特性。例如：行星齿轮传动的齿圈、旋转电机的定转子以及滚动轴承的内外圈等典型构件的模态特性和动力稳定性。

针对上述振动方程的特征，本发明实施例提出了一种弹性振动分析技术，该技术可以得到解析形式的特征值和耦合系数，并据此预测动力稳定性，具体过程如下：

(b1)在随动坐标系下建立动力学模型；

(b2)求解光滑圆环的特征值；

(b3)根据摄动法求解环状周期结构的一阶摄动特征值；

(b4)借助三角函数的运算性质，判断振动波数与离散支撑个数之间的组合关系，然后分类计算环状周期结构的一阶摄动特征值；

(b5)根据得到的环状周期结构的特征值判断模态特性和动力稳定性；

(b6)求解环状周期结构的耦合系数，揭示组合的不稳定规律。

考虑圆环无延展变形的弹性振动解析分析技术的具体步骤如下：

(c1)借助随动坐标系，建立系统的动力学方程；

(c2)求解光滑圆环的特征值。

假设步骤(c1)中的动力学方程的响应为上述公式(6)和公式(7)，内积为公式(8)，将该假设代入步骤(a1)的动力学方程，然后与e^inθ作内积，可得光滑圆环的特征值公式(9)。

根据摄动法求解环状周期结构的一阶摄动特征值，求解步骤参见公式(10)-(14)，根据三角函数的运算特性，参见公式(15)，据此可分析波数和离散支撑个数等基本参数对特征值的影响规律，进而揭示参数与模态特性及稳定性的映射关系。

(c3)以表1中的环状周期结构参数为例，采用数值方法计算特征值和耦合系数。

表1环状周期结构基本参数

(c4)根据步骤(c2)所求光滑圆环的特征值，可得转速对不稳定域的影响规律，具体结果如附图2所示。

(c5)根据步骤(c3)所求的特征值，可预测特征值分裂规律和动力稳定性，具体结果如附图3～5所示。

(c6)根据步骤(c3)所求的耦合系数，可分析m阶波数对组合不稳定的影响，具体结果如附图6所示。

(c7)根据步骤(c3)所求的耦合系数，可分析转速对组合不稳定的影响，具体结果如附图7～9所示。

综上所述，本发明提供了一种预测环状周期结构的模态特性及动力稳定性的解析技术。该技术运用随动坐标系，采用解析方法得到系统的特征值，提高了准确性、计算效率及普适性，更好地满足了工程实际的需求。

本领域技术人员可以理解附图只是一个优选实施例的示意图，上述本发明实施例序号仅仅为了描述，不代表实施例的优劣。

以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。