临近空间高超声速飞行器AHW的弹道预测方法与流程

本发明属于飞行器弹道预测技术领域，具体涉及一种临近空间高超声速飞行器ahw的弹道预测方法。

背景技术：

临近空间高超声速飞行器ahw(advancedhypersonicweapon，ahw)计划的目标是要发展一种能飞行35min、打击6000km处目标的导弹，且落点打击精度在10m以内。ahw助推器为三级，助推到预定高度后，高超声速滑翔体(hgb)与助推器分离，继续攻击预定目标，末段攻击速度可能达马赫数4。采用了更为常见的锥+裙+十字翼的布局，在临近空间远程滑翔和机动飞行能力较强。

目前针对临近空间飞行器ahw的弹道预测是使用singer模型通过卡尔曼滤波进行飞行器状态估计，得到飞行器位置、速度以及加速度的信息，且假设临近空间高超声速飞行器ahw保持姿态角恒定进行后续的弹道预测。但是该种现有方法在临近空间高超声速飞行器ahw有机动时，对飞行器弹道预测结果的误差较大，且误差将以指数形式迅速发散。因此，国内外目前尚没有针对临近空间ahw飞行器有效的弹道预测的方法。

技术实现要素：

本发明的目的是为解决在临近空间高超声速飞行器ahw有机动时，采用现有方法对飞行器弹道的预测结果误差大的问题。

本发明为解决上述技术问题采取的技术方案是：临近空间高超声速飞行器ahw的弹道预测方法，该方法包括以下步骤：

步骤一、建立临近空间高超声速飞行器ahw的状态方程；

步骤二、设计用于临近空间高超声速飞行器ahw状态跟踪的卡尔曼滤波器，利用设计的卡尔曼滤波器实时跟踪高超声速飞行器ahw的状态信息；

步骤三、根据步骤二设计的卡尔曼滤波器获得跟踪结束kt时刻的高超声速飞行器ahw的状态信息，并根据跟踪结束kt时刻的状态信息获得跟踪结束kt时刻的高超声速飞行器ahw的状态估计值；

其中，k为大于0的整数，t为计算周期，一般可取t＝0.01s；将跟踪结束kt时刻的高超声速飞行器ahw的状态估计值作为弹道预测的初值；

步骤四、利用弹道预测的初值求解(k+1)t时刻高超声速飞行器ahw的位置和速度的预测值，并继续利用(k+1)t时刻的位置和速度的预测值来求解(k+2)t时刻高超声速飞行器ahw的位置和速度的预测值；

步骤五、不断重复步骤四的过程，直至获得每个时刻高超声速飞行器ahw的位置和速度的预测值，完成临近空间高超声速飞行器ahw的弹道预测。

本发明的有益效果是：本发明提供了一种临近空间高超声速飞行器ahw的弹道预测方法，本发明针对临近空间高超声速飞行器ahw，考虑目标受气动力等复杂情况的影响，在飞行器质量、参考面积，气动力参数等敌方飞行器参数未知的情况下，基于当前时刻对于位置和速度的预测，通过求解微分方程，对下一时刻的位置及速度进行预测，直至完成弹道预测。相比于传统方法，本发明方法提高了弹道预测精度，减小了弹道预测误差。

采用本发明方法可以使终端位置预报误差小于10km。

附图说明

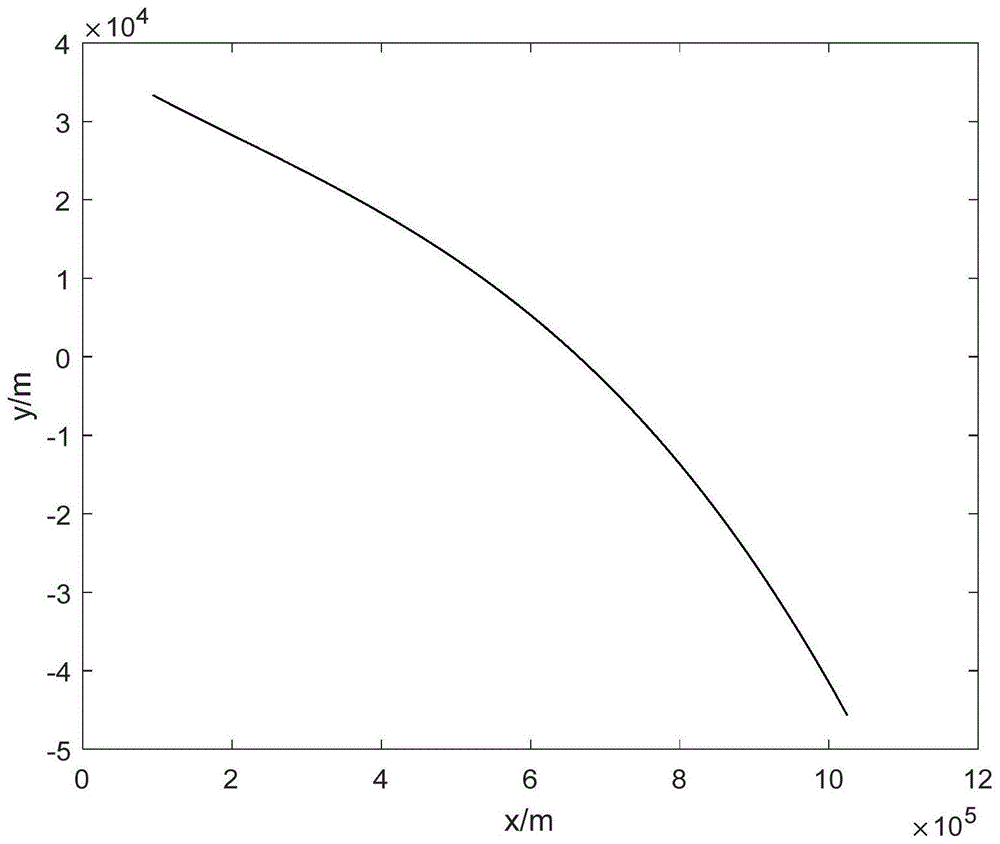
图1为仿真实验中高超声速飞行器ahw在观测惯性坐标系中纵向平面飞行弹道图；

图2为仿真实验中高超声速飞行器ahw在观测惯性坐标系中侧向平面飞行弹道图；

图3为仿真实验中高超声速飞行器ahw的x轴的加速度估计误差图；

图中：t代表时间，axerror代表x轴的加速度估计误差；

图4为仿真实验中高超声速飞行器ahw的y轴的加速度估计误差图；

ayerror代表y轴的加速度估计误差；

图5为仿真实验中高超声速飞行器ahw的z轴的加速度估计误差图；

azerror代表z轴的加速度估计误差；

图6为仿真实验中高超声速飞行器ahw的x轴的速度估计误差图；

vxerror代表x轴的速度估计误差；

图7为仿真实验中高超声速飞行器ahw的y轴的速度估计误差图；

vyerror代表y轴的速度估计误差；

图8为仿真实验中高超声速飞行器ahw的z轴的速度估计误差图；

vzerror代表z轴的速度估计误差；

图9为仿真实验中高超声速飞行器ahw在观测坐标系的x轴向位置估计误差图；

xerror代表x轴的位置估计误差；

图10为仿真实验中高超声速飞行器ahw在观测坐标系的y轴向位置估计误差图；

yerror代表y轴的位置估计误差；

图11为仿真实验中高超声速飞行器ahw在观测坐标系的z轴向位置估计误差图；

zerror代表z轴的位置估计误差；

图12为仿真实验中高超声速飞行器ahw在观测坐标系的x轴向加速度估计、预报与实际值对比图；

图13为仿真实验中高超声速飞行器ahw在观测坐标系的y轴向加速度估计、预报与实际值对比图；

图14为仿真实验中高超声速飞行器ahw在观测坐标系的z轴向加速度估计、预报与实际值对比图；

图15为仿真实验中高超声速飞行器ahw在观测坐标系的x轴向速度估计、预报与实际值对比图；

图16为仿真实验中高超声速飞行器ahw在观测坐标系的y轴向速度估计、预报与实际值对比图；

图17为仿真实验中高超声速飞行器ahw在观测坐标系的z轴向速度估计、预报与实际值对比图；

图18为仿真实验中高超声速飞行器ahw在观测坐标系的x轴向位置估计、预报与实际值对比图；

图19为仿真实验中高超声速飞行器ahw在观测坐标系的y轴向位置估计、预报与实际值对比图；

图20为仿真实验中高超声速飞行器ahw在观测坐标系的z轴向位置估计、预报与实际值对比图；

图21为仿真实验中高超声速飞行器ahw的位置估计、预报与实际值的误差曲线图；

rerror代表估计、预报与实际值的位置误差；

图22为仿真实验中高超声速飞行器ahw终端位置预报误差统计结果图；

rperror代表终端位置预报误差；

图23为飞行器可能落点范围及飞行走廊的示意图。

具体实施方式

具体实施方式一：本实施方式所述的临近空间高超声速飞行器ahw的弹道预测方法，该方法包括以下步骤：

步骤一、建立临近空间高超声速飞行器ahw的状态方程；

步骤二、设计用于临近空间高超声速飞行器ahw状态跟踪的卡尔曼滤波器，利用设计的卡尔曼滤波器实时跟踪高超声速飞行器ahw的状态信息；

步骤三、根据步骤二设计的卡尔曼滤波器获得跟踪结束kt时刻的高超声速飞行器ahw的状态信息，并根据跟踪结束kt时刻的状态信息获得跟踪结束kt时刻的高超声速飞行器ahw的状态估计值；

其中，k为大于0的整数，t为计算周期，一般可取t＝0.01s；将跟踪结束kt时刻的高超声速飞行器ahw的状态估计值作为弹道预测的初值；

步骤四、利用弹道预测的初值求解(k+1)t时刻高超声速飞行器ahw的位置和速度的预测值，并继续利用(k+1)t时刻的位置和速度的预测值来求解(k+2)t时刻高超声速飞行器ahw的位置和速度的预测值；

步骤五、不断重复步骤四的过程，直至获得每个时刻高超声速飞行器ahw的位置和速度的预测值，完成临近空间高超声速飞行器ahw的弹道预测。

具体实施方式二：本实施方式与具体实施方式一不同的是：所述步骤一的具体过程为：

引入3个状态变量zx、zy和zz，且状态变量zx、zy和zz的表达式分别为：

其中：cx0、cy0和cz0分别代表高超声速飞行器ahw在速度坐标系下的x0轴、y0轴和z0轴向的空气动力系数；mt为高超声速飞行器ahw的质量；s为高超声速飞行器ahw的等效参考面积；

选取状态变量x为：

x＝[xyzvxvyvzzxzyzz]^t(2)

其中：x、y和z分别为高超声速飞行器ahw在观测惯性坐标系下x轴、y轴和z轴向的位置坐标；vx、vy和vz分别为高超声速飞行器ahw在观测惯性坐标系下x轴、y轴和z轴向的速度；

则建立临近空间高超声速飞行器ahw的状态方程为：

所述临近空间高超声速飞行器ahw的状态方程包含加速度计算方程、速度计算方程、位置计算方程；

其中：为x的一阶导数，为y的一阶导数，为z的一阶导数，为vx的一阶导数，为vy的一阶导数，为vz的一阶导数，为zx的一阶导数，为zy的一阶导数，为zz的一阶导数；ax、ay和az分别为高超声速飞行器ahw在观测惯性坐标系下x轴、y轴和z轴向的加速度；w1、w2和w3均为高斯白噪声，代表了慢时变的随机游走过程。

具体实施方式三：本实施方式与具体实施方式二不同的是：所述中间变量atx、aty和atz组成的中间变量矩阵以及中间变量gx、gy和gz组成的中间变量矩阵的表达式如下：

其中：ρ为空气密度；代表高超声速飞行器ahw的速度大小；利用弹道坐标系对速度坐标系进行替换，则为由弹道坐标系到观测惯性坐标系的变换矩阵(为由速度坐标系到观测惯性坐标系的变换矩阵，对于轴对称式飞行器，侧向机动一般由偏航通道通过侧滑角进行控制，实际飞行过程中飞行器滚转角一般较小，因而速度坐标系可以用弹道坐标系进行替换，所以，代表由弹道坐标系到观测惯性坐标系的变换矩阵)；μ为引力系数；re为地球半径；

弹道坐标系到观测惯性坐标系的变换矩阵的表达式为：

其中：

具体实施方式四：本实施方式与具体实施方式三不同的是：所述步骤二的具体过程为：所述用于临近空间高超声速飞行器ahw状态跟踪的卡尔曼滤波器的预报方程为：

其中，为卡尔曼滤波器对状态变量x的估计值，表示使用状态变量的估计值下的高超声速飞行器ahw系统状态方程；q为高超声速飞行器ahw系统状态模型误差协方差矩阵；rn为测量误差协方差矩阵；上标^-1代表矩阵求逆运算；上标^t代表矩阵转置运算；h为卡尔曼滤波器的测量矩阵；p为卡尔曼滤波器的协方差矩阵，为p对时间的一阶导数；f为雅克比矩阵；

采用龙格库塔法求解公式(8)，得到中间变量和p(k+1/k)的值；

所述用于临近空间高超声速飞行器ahw状态跟踪的卡尔曼滤波器的测量修正方程为：

其中：i代表单位矩阵，k(k+1)代表卡尔曼滤波器第k+1步的滤波增益矩阵，η(k+1)代表卡尔曼滤波器第k+1步的测量信息，为卡尔曼滤波器第k+1步的估计值，p(k+1)为卡尔曼滤波器第k+1步的协方差矩阵的值；

η(k+1)＝hx+rn(12)

综合公式(8)和公式(11)，获得用于临近空间高超声速飞行器ahw状态跟踪的卡尔曼滤波器，利用设计的卡尔曼滤波器实时跟踪高超声速飞行器ahw的状态信息。

具体实施方式五：本实施方式与具体实施方式四不同的是：所述步骤三的具体过程为：

根据步骤二设计的卡尔曼滤波器获得跟踪结束kt时刻的高超声速飞行器ahw的状态信息，并根据跟踪结束kt时刻的状态信息获得跟踪结束kt时刻的高超声速飞行器ahw的状态估计值如下：

其中：xp(kt)、yp(kt)和zp(kt)为跟踪结束kt时刻的高超声速飞行器ahw在观测惯性坐标系下x轴、y轴和z轴向的位置，vxp(kt)、vyp(kt)和vzp(kt)分别为跟踪结束kt时刻的高超声速飞行器ahw在观测惯性坐标系下x轴、y轴和z轴向的速度；和分别为跟踪结束kt时刻对zx、zy和zz估计值；

由于临近空间飞行器末段的飞行特性，在弹道预测过程中，将状态变量zx、zy和zz作为恒定常值，所以，将状态变量zx、zy和zz分别取为常值和

将xp(kt)、yp(kt)、zp(kt)、vxp(kt)、vyp(kt)、vzp(kt)、和作为弹道预测的初值。

由式(3)至式(5)可知，对于临近空间高超声速飞行器ahw，其在飞行末段的加速度由空气动力和地球引力产生，在高超声速飞行器ahw进入最后下压之前，由于飞行器的姿态角通常变化不大；飞行器高速飞行状态下，速度对空气动力系数的影响较小，因而空气动力系数cx、cy、cz变化不大。

由式(1)可知zx、zy、zz变化较小。因而可以在弹道预测过程中将zx、zy、zz取为常值，该值由跟踪结束时刻的估计值确定。

式(4)中ρ、v、和地球引力对加速度变化影响较大，空气密度ρ只与ahw所在高度有关，而ahw的高度与地球引力大小仅与状态量x、y、z有关，速度v及坐标变换矩阵cvⁱ只与状态vx、vy、vz有关。

即由kt时刻观测惯性坐标系下x轴、y轴和z轴向的位置和速度的预测值就可以获得(k+1)t时刻加速度的预测值，而由(k+1)t时刻加速度的预测值，根据式(3)又可以获得(k+1)t时刻的观测惯性坐标系下x轴、y轴和z轴向的速度和位置的预测值，从而实现迭代计算，进行全程的预测。该过程是一个含有6个参数的微分方程，可使用龙格库塔法求解此微分方程。

具体实施方式六：本实施方式与具体实施方式五不同的是：所述步骤四的具体过程为：

综合公式(3)至公式(7)获得如下的微分方程：

根据xp(kt)、yp(kt)、zp(kt)、vxp(kt)、vyp(kt)、vzp(kt)、和采用龙格库塔法求解微分方程(14)，得到(k+1)t时刻高超声速飞行器ahw的位置和速度在观测惯性坐标系下的预测值；其中：xp((k+1)t)、yp((k+1)t)和zp((k+1)t)代表(k+1)t时刻高超声速飞行器ahw的位置在观测惯性坐标系下x轴、y轴和z轴向的预测值，vxp((k+1)t)、vyp((k+1)t)和vzp((k+1)t)代表(k+1)t时刻高超声速飞行器ahw的速度在观测惯性坐标系下x轴、y轴和z轴向的预测值；

同理，根据xp((k+1)t)、yp((k+1)t)、zp((k+1)t)、vxp((k+1)t)、vyp((k+1)t)、vzp((k+1)t)、和采用龙格库塔法求解微分方程(14)，得到(k+2)t时刻高超声速飞行器ahw的位置和速度在观测惯性坐标系下x轴、y轴和z轴向的预测值。

仿真部分

本次仿真共进行200s，0～60s时刻对临近空间飞行器ahw进行状态估计；

如图1至图23所示，对于攻击方来讲，本发明所设计的临近空间飞行器在攻击目标点时会有末速度和攻击角度的要求，通常要求末速度和攻击角度达到某一最小值。仿真结果表明，若要求末速度大于2mach，攻击角度大于70°的情况下，在进入最终下压点时速度需要在2800m/s左右。在这种实际情况的制约下，临近空间高超声速飞行器ahw在末段的机动能力已经受到了约束限制。若在距目标点1000km处飞行器速度大小及方向已知的情况下，飞行器可能的落点范围约为以此目标点为圆心半径50km的圆形区域。在此情况下，若飞行器最终落点确定，则末段飞行走廊宽度为仅为20km左右(z轴正负方向各10km左右)。飞行器可能落点范围、飞行走廊宽度等关系如图23所示。

在本发明的仿真中，直接将飞行器最终攻击点定为了观测坐标系(即观测惯性坐标系)的原点，因此飞行器最大横向机动范围为20km左右。若飞行器攻击点在可能落点范围内任意取值而与观测坐标系原点不重合，并不会对状态估计与预测的结果产生影响。此外，对于临近空间飞行器的弹道预测，知道该飞行器的大致目标点是必要的，雷达等探测装置通常部署在防御目标附近。同时，进行弹道预测的目的是对临近空间飞行器进行后续的拦截做准备，而只有预测出下压点之前的弹道才具有拦截的意义。如果敌方飞行器的大致攻击范围不确定，飞行器随时可能进入下压段进行攻击，这种情况是难以预测拦截的。由图23可知，在飞行器可能攻击范围限定为50km半径的圆后，最终下压点横向取值范围约为120km，本发明研究的意义在于经过60s时间的状态估计，可通过弹道预测将200s时刻下压点之前120km宽度的走廊范围缩小到小于10km的范围。

在上述条件下，经过100次monte-carlo仿真得到的临近空间高超声速飞行器ahw最终位置预报误差的统计结果如图22所示，统计计算得出终端位置预报误差均小于10km。

本发明的上述算例仅为详细地说明本发明的计算模型和计算流程，而并非是对本发明的实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动，这里无法对所有的实施方式予以穷举，凡是属于本发明的技术方案所引伸出的显而易见的变化或变动仍处于本发明的保护范围之列。