一种长大隧道车速分布的环境因素水平智能优化方法与流程

本发明属于道路工程与交通信息工程技术邻域，尤其涉及一种长大隧道车速分布的环境因素水平智能优化方法。

背景技术：

长大隧道内的车流速度分布具有较强的时空差异性，此差异性具体表现在85％位车速、平均车速以及车速标准差这三项指标上。在时间上，随着隧道运营时间的推移，车速分布会发生变化，且在每日的不同时段内，车速分布亦会表现出显著的差异性。在空间上，长大隧道的进、出口具有黑白洞效应，故车速低、离散度小，而长大隧道的中部路段车速高、离散度大。隧道的通行效率以及安全水平与车流速度和离散度密切相关，车流速度低时易形成“瓶颈”降低通行效率，车流离散度大时追尾事故风险大，安全水平低。而车速分布受到诸多环境因素的影响，改变环境因素的水平势必能影响车速分布，但当前尚无一种有效的模型可以建立环境因素与车速分布之间复杂的非线性关系，并利用此关系求得管理者期望车速分布下的各项环境因素最佳水平。

为了实现大样本数据的非线性回归，目前多采用人工神经网络来进行监督学习。极限学习机是一类基于前馈神经网络的机器学习算法，其主要特点是隐含层节点参数可以是随机的或认为给定的，且不需要调整，学习过程仅需计算权重，具有学习效率高和泛化能力强的特点。为了求得期望车速分布下各环境因素的水平，即求解多元非线性函数极值，当前常采用启发式算法，其中粒子群算法就是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的简化模型，能利用群体中的个体对信息的共享，使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

综上所述，本发明提出了一种影响长大隧道车速分布的环境因素水平人工智能计算方法，以环境因素和车速的历史观测数据为学习样本，通过极限学习机神经网络构建环境因素与车速分布之间的非线性映射关系，并利用粒子算法求解期望车速分布下的各项环境因素最佳水平。

技术实现要素：

本发明根据环境因素与车速分布之间具有非线性映射关系作为理论基础，结合人工智能算法，提出了一种长大隧道车速分布的环境因素水平智能优化方法，通过极限学习机来构建环境因素与车速分布之间的非线性映射关系，再利用粒子群算法求解管理者期望车速分布下的各环境因素的最佳水平，即可获得实现管理者期望车速分布所需的各项环境因素水平。

本发明的技术方案为一种长大隧道车速分布的环境因素水平智能优化方法，具体包括以下步骤：

步骤1：将历史采集的连续多天的环境因素和车速分布数据作为学习样本；

步骤2：根据历史连续多天采集得到的环境因素与车速分布历史数据构建极限学习机神经网络；

步骤3：粒子群算法求解管理者期望车速分布下的各项环境因素最佳水平。

作为优选，步骤1中所述将历史采集的连续多天的环境因素和车速分布数据作为学习样本为：

采用单隐含层的极限学习机神经网络，输入层有n个神经元，对应n个环境因素输入变量；隐含层有l个神经元；输出层有m个神经元，分别对应m个输出变量；

将一天24h划分为s个时段(s为正整数)，在每个时段末采集环境因素和车速分布指标的数据，每个时段采集的数据可构成一个学习样本，n项环境因素对应n个输入，m项车速分布指标对应m个输出；

输入样本ips,i,q表示第s(s＝1,2,3,…,s)个时段上采集的第i(i＝1,2,3,...,n)项环境因素在第q(q＝1,2,3,…,q)天中的水平；ops,j,q表示第s(s＝1,2,3,…,s)个时段内采集的第j(j＝1,2,3,...,m)项车速分布指标在第q(q＝1,2,3,…,q)天的值，作为输出样本；

作为优选，步骤2中所述构建极限学习机神经网络具体如下：

第s(s＝1,2,3,…,s)个时段的学习样本共有q个，对于第s时段的神经网络映射fs:x→y的构建方法如下：

第s时段具有q个样本的训练集输入矩阵xs和输出矩阵ys分别为：

其中，xs,i,q表示历史数据中第s(s＝1,2,3,…,s)个时段上第i(i＝1,2,…,n)个输入在第q(q＝1,2,…,q)个学习样本中的值；

ys,j,q表示历史数据中第s(s＝1,2,3,…,s)个时段上第j(j＝1,2,…,m)个输出在第q(q＝1,2,…,q)个学习样本中的值；

xs,i,q与ipq,s,i、ys,j,q与opq,s,j具有如下关系

xs,i,q＝ips,i,q，ys,j,q＝ops,j,q

第s时段的输入层与隐含层之间的连接权值为ws，隐含层与输出层之间的连接权值为βs，隐含层神经元的阈值为bs：

其中，ws,e,i表示历史数据中第s时段上第e(e＝1,2,…,l)个隐含层神经元与第i(i＝1,2,…,n)个输入层神经元之间的连接权值；βs,e,j表示历史数据中第s时段上第e个隐含层神经元与第j(j＝1,2,…,m)个输出层神经元之间的连接权值；bs,e表示第s时段上第e个隐含层神经元的偏移值；

第s时段的隐含层神经元激活函数为gs(x)，输出为ts，ts,q为(m×1)列向量，表示第s时段上第q个输入样本在网络中的计算输出值：

t＝[t1,t2,...,tq]m×q

式中，tj,q表示第q个输入样本在第j(j＝1,2,…,m)个输出层神经元的计算输出值；ws,e＝[ws,e,1,ws,e,2,…ws,e,n]1×n为行向量，xs,q＝[xs,1,q,xs,2,q,…,xs,n,q]^t为列向量，其余参数定义同上；

网络输入与输出的关系可由下式表示：

化简为：

式中为矩阵βs的转置，ts^t为矩阵ts的转置，矩阵[bs]l×q＝bs×[1,1,…1]1×q，[ηs]q×l为第s时段的隐含层输出矩阵，hs＝[gs(wsxs+bs)]^t具体形式如下：

当隐含层神经元个数与训练样本数相等时，即l＝q时，对于q个不同的训练样本集

其中xs,q＝[xs,1,q,xs,2,q,…xs,n,q]^t∈rⁿ，ys,q＝[ys,1,q,ys,2,q,…,ys,m,q]^t∈r^m，若激活函数gs:r→r满足在任意区间上无限可微，那么对于任意在rⁿ和r空间的任何区间内根据任意连续的概率分布随机生成ws,e和bs,e，则其隐含层输出矩阵hs以概率1可逆，且有||ηsβs-ts^t||＝0以概率1成立。那么对于任意的ws和bs，此神经网络均可零误差逼近训练样本，即：

当训练样本q比较大时，为减少计算量，隐含层神经元个数l的取值通常小于q，给定一个任意小的正数ε＞0和任意q个不同的训练样本集其中xs,q＝[xs,1,q,xs,2,q,…xs,n,q]^t∈rⁿ，ys,q＝[ys,1,q,ys,2,q,…,ys,m,q]^t∈r^m，若激活函数gs:r→r满足在任意区间上无限可微，那么对于任意在rⁿ和r空间的任何区间内根据任意连续的概率分布随机生成ws,e和bs,e，存在一个含有l(l≤q)个隐含层神经元的前馈神经网络，使得||ηsβs-ts^t||＜ε以概率1成立。此神经网络的训练误差可以逼近一个任意的ε＞0，即：

隐含层的激活函数gs(x)采用在区间上无限可微的sigmoid函数

因此，当激活函数gs(x)无限可微时，ws和bs在训练前可随机选取，且在训练过程中保持不变，而隐含层与输出层之间的连接权值βs，可通过求解如下极小范数方程的最小二乘解获得：

其解为：

式中，ηs⁺为隐含层输出矩阵ηs的moore-penrose增广逆，通常采用正交法计算ηs⁺：

当ηs^tηs为非奇异矩阵时，ηs⁺＝ηs^-1[(ηs^tηs)^-1-ηs^t]；

当ηsηs^t为非奇异矩阵时，ηs+＝ηs^t(ηsηs^t)^-1；

由上述方式单隐含层的极限学习机神经网络，此网络能拟合得到第s时段输入向量xs,q和输出向量ys,q之间的非线性映射关系fs:xs,q→ys,q；

对于任意输入向量xs,q，将此网络的计算输出向量ts,q记作ts,q＝fs(xs,q)；

作为优选，步骤3中所述粒子群算法求解管理者期望车速分布下的各项环境因素最佳水平为：

若在该路段的第s时段内，管理者期望的车速分布为[es]m×1，建立目标函数，通过调节第s时段的环境因素水平[is]n×1使路段上的实际车速分布[os]m×1逼近期望车速分布es，第s时段的目标函数表示如下

minfs(os)＝||es-os||

根据映射关系fs:is→os求解目标函数可得环境因素的最佳水平is^*。

在第s时段内影响车速的n个环境因素中，其水平为is＝[ds,1,ds,2,…,ds,n]^t，ds,i(i＝1,2,…,n)为第s时段的第i项环境因素水平；is的区间取值上限为[ucls]n×1＝[ucls,1,ucls,2,…,ucls,n]^t，ucls,i为第s时段第i(i＝1,2,…,n)个因素水平的上限；is的区间取值下限为[lcls]n×1＝[lcls,1,lcls,2,…,lcls,n]^t，lcls,i为第s时段第i个因素水平的取值下限，可作为求解目标函数的约束条件之一

lcls,i≤ds,i≤ucls,i

通过粒子群算法求解上述目标函数极值。

步骤3.1：在n维搜索空间出初始化n个粒子，形成初代(进化代数r＝0)种群其中第k(k＝1,2,…,n)个粒子表示第s时段的一个n维向量ds,k,i为初代种群中第s时段上第k个粒子在第i维搜索空间中的位置，向量可表示一个潜在解；

步骤3.2：根据第s时段神经网络的映射关系fs:is→os计算第r代第k个粒子在网络的输出进而可算得其目标函数值

由于此问题为最小值问题，而个体适应度为效益型指标，故可令第s时段的适应度函数gs(x)＝-fs(x)，则第s时段的个体适应度

比较第s时段内该代种群中所有粒子的适应度函数值，得适应度函数值最大的为第e(e＝1,2,…,n)个粒子，其位置为is,e^r，则第s时段内第r代的个体极值位置为ps^r＝is,e^r，种群极值位置为zs^r计算方法为：若r＝0，则zs^r＝is,e^r；若r≥1，则种群极值位置zs^r取值为zs^r-1和ps^r两位置上适应度函数值较大者；

步骤3.3：进化代数更新r＝r+1，若代数r超过最大进化代数mg，即r＞mg，则转至步骤3.4；否则继续执行以下操作。

根据上一代中极值个体的位置更新种群内其他粒子的位置

其中，α为惯性权重；c1为向个体极值移动的加速度因子，取非负常数；c2为向种群极值移动的加速度因子，取非负常数；λ1为区间[0,1]内服从均匀分布的随机数，λ2为区间[0,1]内服从均匀分布的随机数；为第s时段内第r代中第k个粒子的速度向量，vs,k,i为第s时段内第k个粒子在第i维空间中的搜索速度；速度的区间上限为[lvs]1×n＝[lvs,1,lvs,2,…,lvs,n]^t，lvs,i为第s时段内第i维空间中搜索速度的上限；速度的区间下限为[uvs]1×n＝[uvs,1,uvs,2,…,uvs,n]^t，uvs,i为第s时段内第i维空间中搜索速度的下限；为第s时段内第(r-1)代种群中第k个粒子的位置向量，为第s时段内第r代种群中第k个粒子的位置向量；位置向量的取值区间上限为[ucls]n×1＝[ucls,1,ucls,2,…,ucls,n]^t，ucls,i为第s时段第i个因素水平的上限；位置向量的取值下限为[lcls]n×1＝[lcls,1,lcls,2,…,lcls,n]^t，lcls,i为第s时段第i个因素水平的取值下限

转至步骤3.2；

步骤3.4：由第s时段上神经网络的映射关系fs:is→os计算末代(r＝mg)第k个粒子在网络的输出进而可算得目标函数值个体适应度为

比较末代r＝mg种群中所有粒子的适应度函数值，得第s时段上适应度函数值最大的为第e(e＝1,2,…,n)个粒子，其位置为则末代种群的个体极值位置种群极值位置zs^r取值为zs^r-1和ps^r两位置上适应度函数值较大者。

由粒子群算法求解得到第s时段上各环境因素最佳水平is^*。

本发明提出了一种影响长大隧道车速分布的环境因素水平人工智能计算方法，可以通过神经网络建立环境因素与车速分布之间的非线性关系，并用粒子群算法求解管理者期望车速分布下各环境因素所需达到的水平。

附图说明

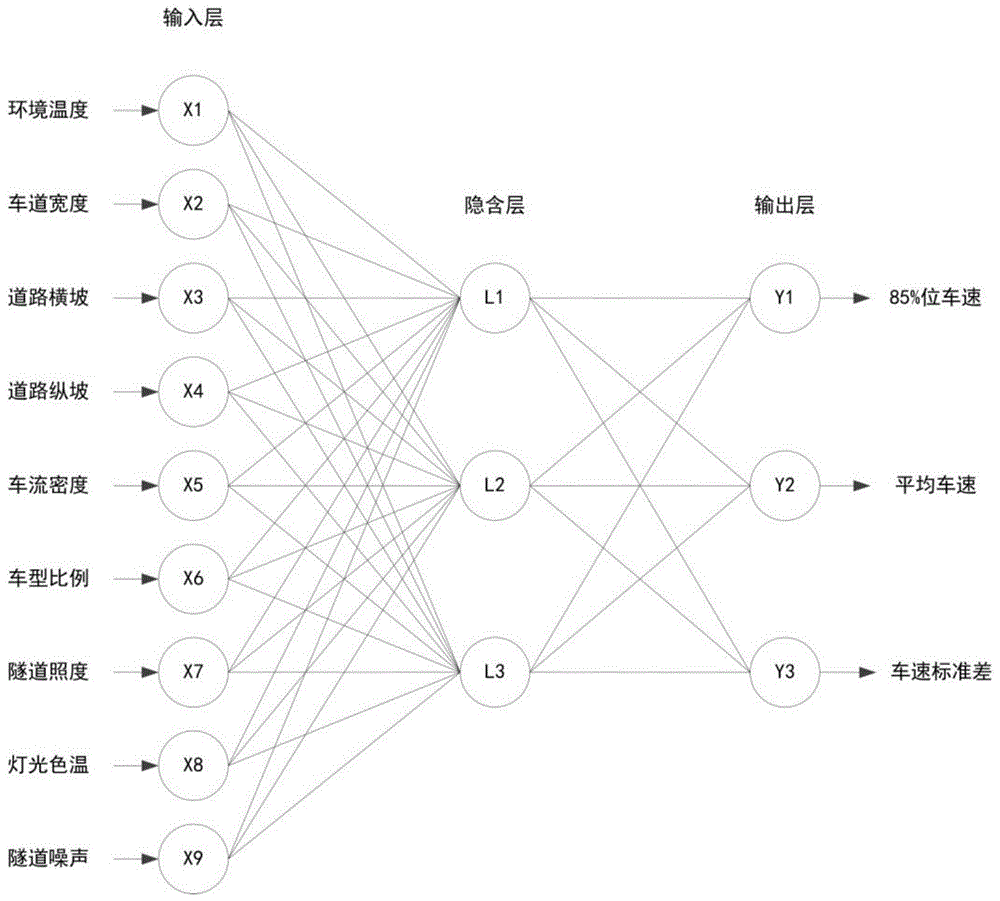
图1：极限学习机神经网络结构；

图2：粒子群算法求解流程图；

图3：方法流程图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

下面结合图1至图2介绍本发明的具体实施方式为一种长大隧道车速分布的环境因素水平智能优化方法，包括以下步骤：

步骤1：将历史采集的连续多天的环境因素和车速分布数据作为学习样本；

步骤1中所述将历史采集的连续多天的环境因素和车速分布数据作为学习样本为：

采用单隐含层的极限学习机神经网络，输入层有9个神经元，对应9个环境因素输入变量，即环境温度、车道宽度、道路横坡、道路纵坡、车流密度、车型比例、隧道照明、灯光色温和隧道噪声的观测值；隐含层有3个神经元；输出层有3个神经元，分别对应3个输出变量，即85％位车速、平均车速和车速标准差；

将一天24h划分为12个时段，在每个时段末采集环境因素和车速分布指标的数据，每个时段采集的数据可构成一个学习样本，9项环境因素对应9个输入，3项车速分布指标对应3个输出；

输入样本ips,i,q表示第s(s＝1,2,3,…,12)个时段上采集的第i(i＝1,2,3,...,9)项环境因素在第q(q＝1,2,3,…,365)天中的水平；ops,j,q表示第s(s＝1,2,3,…,12)个时段内采集的第j(j＝1,2,3)项车速分布指标在第q(q＝1,2,3,…,365)天的值，作为输出样本；

步骤2：根据历史连续365天采集得到的环境因素与车速分布历史数据构建极限学习机神经网络；

步骤2中所述构建极限学习机神经网络具体如下：

第s(s＝1,2,3,…,12)个时段的学习样本共有365个，对于第s时段的神经网络映射fs:x→y的构建方法如下：

第s时段具有365个样本的训练集输入矩阵xs和输出矩阵ys分别为：

其中，xs,i,q表示历史数据中第s(s＝1,2,3,…,12)个时段上第i(i＝1,2,…,9)个输入在第q(q＝1,2,…,365)个学习样本中的值；

ys,j,q表示历史数据中第s(s＝1,2,3,…,12)个时段上第j(j＝1,2,3)个输出在第q(q＝1,2,…,365)个学习样本中的值；

xs,i,q与ipq,s,i、ys,j,q与opq,s,j具有如下关系：

xs,i,q＝ips,i,q，ys,j,q＝ops,j,q

第s时段的输入层与隐含层之间的连接权值为ws，隐含层与输出层之间的连接权值为βs，隐含层神经元的阈值为bs：

其中，ws,e,i表示历史数据中第s时段上第e(e＝1,2，3)个隐含层神经元与第i(i＝1,2,…,9)个输入层神经元之间的连接权值；βs,e,j表示历史数据中第s时段上第e个隐含层神经元与第j(j＝1,2,3)个输出层神经元之间的连接权值；bs,e表示第s时段上第e个隐含层神经元的偏移值；

第s时段的隐含层神经元激活函数为gs(x)，输出为ts，ts,q为(3×1)列向量，表示第s时段上第q个输入样本在网络中的计算输出值：

t＝[t1,t2,...,t365]3×365

式中，tj,q表示第q个输入样本在第j(j＝1,2,3)个输出层神经元的计算输出值；ws,e＝[ws,e,1,ws,e,2,…,ws,e,9]1×9为行向量，xs,q＝[xs,1,q,xs,2,q,…,xs,9,q]^t为列向量，其余参数定义同上；

网络输入与输出的关系可由下式表示：

化简为：

ηsβs＝ts^t

式中βs^t为矩阵βs的转置，ts^t为矩阵ts的转置，有[bs]3×365＝bs×[1,1,…1]1×365，[ηs]365×3为第s时段的隐含层输出矩阵，hs＝[gs(wsxs+bs)]^t具体形式如下：

当隐含层神经元个数与训练样本数相等时，即l＝q＝365时，对于365个不同的训练样本集

其中，xs,q＝[xs,1,q,xs,2,q,…xs,9,q]^t∈r⁹，ys,q＝[ys,1,q,ys,2,q,ys,3,q]^t∈r³，若激活函数gs:r→r满足在任意区间上无限可微，那么对于任意在r⁹和r空间的任何区间内根据任意连续的概率分布随机生成ws,e和bs,e，则其隐含层输出矩阵hs以概率1可逆，且有||ηsβs-τs^t||＝0以概率1成立。那么对于任意的ws和bs，此神经网络均可零误差逼近训练样本，即：

当训练样本q比较大时，为减少计算量，隐含层神经元个数l的取值通常小于q，给定一个任意小的正数ε(ε＝0.001)和任意q(q＝365)个不同的训练样本集xs,q＝[xs,1,q,xs,2,q,…xs,9,q]^t∈r⁹，ys,q＝[ys,1,q,ys,2,q,ys,3,q]^t∈r³，若激活函数gs:r→r满足在任意区间上无限可微，那么对于任意在r⁹和r空间的任何区间内根据任意连续的概率分布随机生成ws,e和bs,e，存在一个含有l(l≤q)个隐含层神经元的前馈神经网络，使得||ηsβs-ts^t||＜ε以概率1成立。此神经网络的训练误差可以逼近一个任意的ε＞0，即：

隐含层的激活函数gs(x)采用在区间上无限可微的sigmoid函数

因此，当激活函数gs(x)无限可微时，ws和bs在训练前可随机选取，且在训练过程中保持不变，而隐含层与输出层之间的连接权值βs，可通过求解如下极小范数方程的最小二乘解获得：

其解为：

式中，ηs⁺为隐含层输出矩阵ηs的moore-penrose增广逆，通常采用正交法计算ηs⁺：

当ηs^tηs为非奇异矩阵时，ηs⁺＝ηs^-1[(ηs^tηs)^-1-ηs^t]；

当ηsηs^t为非奇异矩阵时，ηs⁺＝ηs^t(ηsηs^t)^-1；

由上述方式单隐含层的极限学习机神经网络，此网络能拟合得到第s时段输入向量xs,q和输出向量ys,q之间的非线性映射关系fs:xs,q→ys,q；

对于任意输入向量xs,q，将此网络的计算输出向量ts,q记作ts,q＝fs(xs,q)；

步骤3：粒子群算法求解管理者期望车速分布下的各项环境因素最佳水平。

步骤3中所述粒子群算法求解管理者期望车速分布下的各项环境因素最佳水平为：

若在该路段的第s时段内，管理者期望的车速分布为[es]3×1，建立目标函数，通过调节第s时段的环境因素水平[is]9×1使路段上的实际车速分布[os]3×1逼近期望车速分布es，第s时段的目标函数表示如下

minfs(os)＝||es-os||

根据映射关系fs:is→os求解目标函数可得环境因素的最佳水平is^*。

在第s时段内影响车速的9个环境因素中，其水平为is＝[ds,1,ds,2,…,ds,9]^t，ds,i为第s时段的第i(i＝1,2,…,9)项环境因素水平；is的区间取值上限为[ucls]9×1＝[ucls,1,ucls,2,…,ucls,9]^t，ucls,i为第s时段第i(i＝1,2,…,9)个因素水平的上限；is的区间取值下限为[lcls]9×1＝[lcls,1,lcls,2,…,lcls,9]^t，lcls,i为第s时段第i个因素水平的取值下限，可作为求解目标函数的约束条件之一

lcls,i≤ds,i≤ucls,i

通过粒子群算法求解上述目标函数极值。

步骤3.1：在9维搜索空间出初始化n(n＝200)个粒子，形成初代(进化代数r＝0)种群其中第k(k＝1,2,…,200)个粒子表示第s时段的一个9维向量ds,k,i为初代种群中第s时段上第k个粒子在第i维搜索空间中的位置，向量可表示一个潜在解；

步骤3.2：根据第s时段神经网络的映射关系fs:is→os计算第r代第k个粒子在网络的输出进而可算得其目标函数值

由于此问题为最小值问题，而个体适应度为效益型指标，故可令第s时段的适应度函数gs(x)＝-fs(x)，则第s时段的个体适应度

比较第s时段内该代种群中所有粒子的适应度函数值，得适应度函数值最大的为第e(e＝1,2,…,200)个粒子，其位置为则第s时段内第r代的个体极值位置为种群极值位置为zs^r计算方法为：若r＝0，则若r≥1，则种群极值位置zs^r取值为zs^r-1和ps^r两位置上适应度函数值较大者；

步骤3.3：进化代数更新r＝r+1，若代数r超过最大进化代数mg，即r＞mg，则转至步骤3.4；否则继续执行以下操作。

根据上一代中极值个体的位置更新种群内其他粒子的位置

其中，α为惯性权重；c1为向个体极值移动的加速度因子，取非负常数；c2为向种群极值移动的加速度因子，取非负常数；λ1为区间[0,1]内服从均匀分布的随机数，λ2为区间[0,1]内服从均匀分布的随机数；为第s时段内第r代中第k个粒子的速度向量，vs,k,i为第s时段内第k个粒子在第i维空间中的搜索速度；速度的区间上限为[lvs]1×9＝[lvs,1,lvs,2,…,lvs,9]^t，lvs,i为第s时段内第i维空间中搜索速度的上限；速度的区间下限为

[uvs]1×9＝[uvs,1,uvs,2,…,uvs,9]^t，uvs,i为第s时段内第i维空间中搜索速度的下限；为第s时段内第(r-1)代种群中第k个粒子的位置向量，为第s时段内第r代种群中第k个粒子的位置向量；位置向量的取值区间上限为[ucls]9×1＝[ucls,1,ucls,2,…,ucls,9]^t，ucls,i为第s时段第i个因素水平的上限；位置向量的取值下限为[lcls]9×1＝[lcls,1,lcls,2,…,lcls,9]^t，lcls,i为第s时段第i个因素水平的取值下限

转至步骤3.2；

步骤3.4：由第s时段上神经网络的映射关系fs:is→os计算末代(r＝mg)第k个粒子在网络的输出进而可算得目标函数值个体适应度为

比较末代r＝mg种群中所有粒子的适应度函数值，得第s时段上适应度函数值最大的为第e(e＝1,2,…,200)个粒子，其位置为则末代种群的个体极值位置种群极值位置zs^r取值为zs^r-1和ps^r两位置上适应度函数值较大者。

由粒子群算法求解得到第s时段上各环境因素最佳水平is^*。

应当理解的是，上述针对较佳实施例的描述较为详细，并不能因此而认为是对本发明专利保护范围的限制，本领域的普通技术人员在本发明的启示下，在不脱离本发明权利要求所保护的范围情况下，还可以做出替换或变形，均落入本发明的保护范围之内，本发明的请求保护范围应以所附权利要求为准。