一种面向磁共振扩散加权图像的非局部均值平滑方法与流程

本发明涉及磁共振扩散加权图像处理技术领域，尤其涉及一种面向磁共振扩散加权图像的非局部均值平滑方法。

背景技术：

磁共振扩散成像是目前唯一能够在活体上测量组织内水分子扩散运动与成像的无创方法，它通过测量和量化组织中水分子的扩散信息来探测组织的微观结构。水分子沿不同方向的扩散信息包含在一组不同扩散梯度方向的扩散加权图像(diffusionweightedimage，dwi)中，通过对扩散函数进行建模可以解析出每个体素内的纤维结构信息(主要是纤维的走向)。根据每个体素内的纤维走向，利用纤维束追踪技术可重建出组织纤维束的整体三维结构，并可从中提取有效的临床统计特征，从而用于医疗诊断及相关研究等。

扩散张量成像(diffusiontensorimaging，dti)是最早提出的一种扩散模型，目前已被广泛用于临床和医学研究中。这种建模方法虽然简单、稳定，但所采用的二阶对称张量仅能描述体素内的单一平均纤维走向，而无法用于描述存在纤维交叉、分叉等体素内复杂纤维结构。

目前，已有一些方法能够通过更复杂的模型来估计体素内的多个纤维走向，从而解决扩散张量成像方法的限制。这些方法主要包括：多张量模型、高阶扩散张量、q-ball成像、扩散谱成像、球面反卷积(sphericaldeconvolution，sd)、独立分量分析、混合扩散成像等。其中，基于sd的方法由于具备不需指定纤维分布的数量、计算效率高且能够在低角分辨率成像条件下估计体素内纤维走向分布等优点，得到了较广泛的应用，但是基于sd的方法对噪声非常敏感。

技术实现要素：

本发明提供了一种面向磁共振扩散加权图像的非局部均值平滑方法，可以解决现有sd方法直接用于体素内纤维结构估计时易受噪声影响导致估计结果准确性差的问题。

一种面向磁共振扩散加权图像的非局部均值平滑方法，包括以下步骤：

s1，选取滤波参数h，邻域范围rv，rn，对于每个体素pi的每个扩散加权梯度方向gj的磁共振扩散加权信号s(pi，gj)进行s2和s3的平滑操作；h的取值范围是1-20，rv的取值范围是8-15，rn的取值范围是3-7；

s2，对于体素pi的rv×rv×rv邻域vpi中的每个体素pk，按方程(1)计算pk的不同扩散加权梯度方向gl的扩散加权信号对s(pi，gj)的权重ω(pi，gj，pk，gl)；

方程(1)中，npi和npk分别为体素pi和pk的rn×rn×rn邻域，zd为归一化常数，距离dis按方程(2)计算：

方程(2)中，nd为邻域npi中体素的数量，其值等于邻域npk中体素的数量，qm和rm分别为邻域npi和npk中的第m个体素，距离δ按方程(3)计算：

s3，按方程(4)计算对s(pi，gj)进行非局部均值平滑；

方程(4)中，g为所有扩散加权梯度方向的集合。

本发明提供一种面向磁共振扩散加权图像的非局部均值平滑方法，本发明方法与sd方法结合使用可以有效克服现有sd方法直接用于体素内纤维结构估计时易受噪声影响导致估计结果准确性差的问题；能够有效的提高体素内纤维结构估计结果的准确性。本发明方法与sd方法结合使用估计得到的体素内纤维结构与直接采用sd方法相比准确性提高了约200％；与采用经典的非局部均值法(nlm)对扩散加权图像平滑后再采用sd方法(nlm+sd)估计得到体素内纤维结构相比准确性提高了约36％。

附图说明

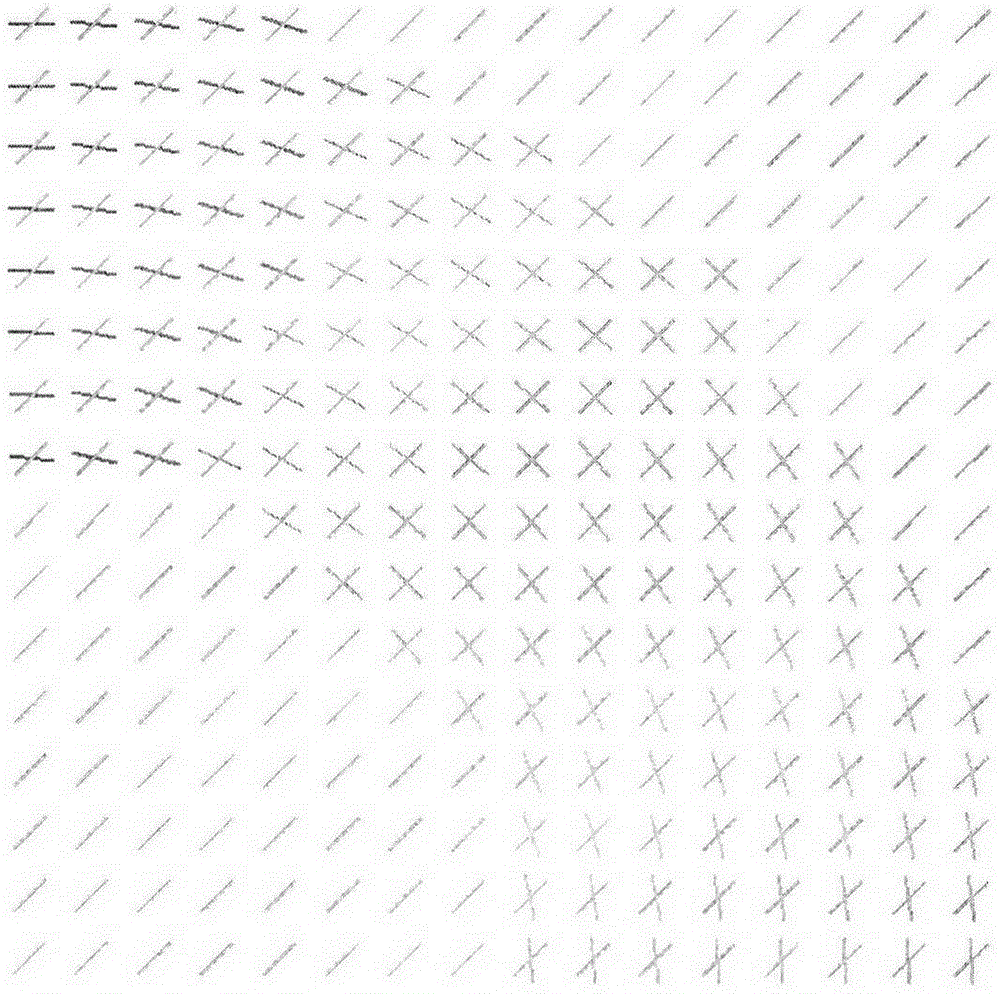
图1为本发明实施例所提供仿真数据的实际体素内纤维结构示意图；

图2为直接采用sd方法得到的体素内纤维结构示意图；

图3为采用nlm+sd方法得到的体素内纤维结构示意图；

图4为采用本发明方法结合sd方法得到的体素内纤维结构示意图。

具体实施方式

下面结合附图，对本发明的一个具体实施方式进行详细描述，但应当理解本发明的保护范围并不受具体实施方式的限制。

本实施例中采用高斯混合模型法模拟生存一组分辨率为16×16的磁共振扩散加权图像仿真数据，该组数据包含30个不同扩散加权梯度方向的磁共振扩散加权图像，扩散敏感因子b值为1000，其各个体素的实际纤维走向如图1所示，图中的每个线段表示其所在体素中纤维的一个走向。在生成的仿真数据中加入一定强度的莱斯噪声，得到一组信噪比25的仿真磁共振扩散加权图像数据。使用本发明面向磁共振扩散加权图像的非局部均值平滑方法对该组含噪数据进行处理的步骤如下：

s1，选取滤波参数h，邻域范围rv，rn，对于每个体素pi的每个扩散加权梯度方向gj的磁共振扩散加权信号s(pi，gj)进行步骤s2和步骤s3的平滑操作；在本实施例中，h取值为7，rv取值为10，rn取值为5。

s2，对于体素pi的rv×rv×rv邻域vpi中的每个体素pk，按方程(1)计算pk的不同扩散加权梯度方向gl的扩散加权信号对s(pi，gj)的权重ω(pi，gj，pk，gl)；

方程(1)中，npi和npk分别为体素pi和pk的rn×rn×rn邻域，zd为归一化常数，距离dis按方程(2)计算，

方程(2)中，nd为邻域npi中体素的数量，其值等于邻域npk中体素的数量，qm和rm分别为邻域npi和npk中的第m个体素，距离δ按方程(3)计算；

s3，按方程(4)计算对s(pi，gj)进行非局部均值平滑；

方程(4)中，g为所有扩散加权梯度方向的集合。

s4，根据经上述步骤平滑后的磁共振扩散加权数据，使用sd方法进行体素内纤维结构估计。

直接采用sd方法得到的体素内纤维结构如图2所示，采用经典的非局部均值法(nlm)对扩散加权图像平滑后再采用sd方法(nlm+sd)得到的体素内纤维结构如图3所示，采用本发明方法结合使用sd方法得到的体素内纤维结构如图4所示。图2、图3和图4所示结果的平均角度误差分别为14.8度、7.5度和4.8度。本发明方法结合使用sd方法与直接使用sd方法和nlm+sd方法相比，精度分别提高了约200％和36％。

以上公开的仅为本发明的几个具体实施例，但是，本发明实施例并非局限于此，任何本领域的技术人员能思之的变化都应落入本发明的保护范围。