一种软组织监督变形算法的制作方法

本发明涉及一种软组织监督变形算法，具体涉及与机器学习相结合的软组织变形算法。

背景技术：

近年来，随着虚拟现实技术的不断发展，通过虚拟现实平台模拟手术训练得到可能。虚拟手术给予医护人员极大的便利，他们可以使用该技术进行反复的模拟练习，提升自己的技术。目前的虚拟手术通过建模、渲染、计算将模拟手术的过程呈现在平台上。软组织的变形模型分为运动模型与物理模型两大类，其中物理模型从物体的受力情况出发，通过调整质点的位置使系统达到平衡，并得到该状态下的最终变性结果，更真实地反映了软组织受力后的形变情况，但仿真速度较慢。物理模型又包括弹簧质点模型、有限元模型、无限元模型等，其中弹簧质点模型适用于对时间要求严格而对精度要求不高的场合，有限元模型适用于对计算精度要求严格而对时间要求不高的场合。然而，目前的弹簧质点模型计算速度与精度均不大理想，阻碍了平台模拟手术训练的发展。

技术实现要素：

发明目的：本发明的目的是为了解决以上问题，本发明提出一种软组织监督变形算法，该方法通过将软组织变形算法与机器学习相结合，通过构造目标函数的形式大大减少了计算量，且在数据搜索后细化网格，提高精度。

技术方案：为了实现以上目的，本发明所述的一种软组织监督变形算法，包括步骤：

第一步：第一次数据检索并复制，采用广度优先搜索算法采集软组织的数据信息，并基于弹簧质点模型建立软组织的物理模型；

第二步：局部细化网格，采用全局最长边平分法对物理模型进行网格细化，找出网格数据中的所有边，判断每条边是否满足平分条件，将所有需要被平分的边加入集合s，对s中的边按照长度的大小进行排序，依次取出s中最长的边并在其中点处插入新的节点，同时按照插入点剖分相应的三角面片，循环计算直到s为空，每次剖分结束后均需要判断新生成的边是否满足剖分条件，若满足则按照长度大小插入s中，保持s有序；需要剖分的边满足条件为：

其中，qij为连接知的边的长度，f函数为网格节点密度需要满足的条件，为质点i的空间坐标，为质点j的空间坐标；

第三步：第二次数据搜索并修正，对细化后的网格进行第二次搜索，将细化后位于物理模型外部的网格数据剔除；

第四步：网格变形，依据步骤三所述的物理模型，对其中的各个质点进行初始化，构建模型的初始状态，该模型中每个质点与相连质点ni和nj间的内力为：

其中，是质点ni与质点nj之间的内力，kij是连接质点ni和质点nj的弹簧的弹性系数，是弹簧当前长度减弹簧不受力时的静止长度，其中lij表示弹簧当前长度，表示连接质点ni和质点nj的弹簧不受力时的静止长度，是从质点ni指向质点nj的单位向量；

其中，l′ij为调整后的弹簧长度，参数b用来调控kij随弹簧长度变化而变化的速度，lij为弹簧当前长度，lmin为网格中长度最小的边，lmax为弹簧中长度最大的边，e为弹簧的弹性模量，参数d用来避免长度接近lmin的边的弹性系数过大；

包含n个质点的弹簧质点模型在任意时刻t包含n个偏微分方程，每个方程描述一个质点的运动状态：

其中，mi是质点ni的质量，是质点ni的加速度矢量，ci是质点ni的阻尼系数，是质点ni的速度矢量，σ(i)代表系统中所有与ni邻接的质点的符号，是质点ni的空间坐标，是质点nj的空间坐标，是该质点ni受到的重力，是重力加速度矢量，是作用在ni上的所有外力的矢量和；

弹簧质点模型采用准静态仿真方法计算，

其中，与分别表示质点ni与质点nj的位置坐标；

设s为所有非控制点的符号集合，δ为常数时间间隔，在每个时刻t＝kδ，k＝1，2，...，通过准静态方程求得所有非控制点的位置信息，在时间间隔δ内，重复下述步骤(1)、(2)，实现网格变形：

获得所有控制点的数据信息，对每个i∈s，有：

其中，为每个节点上的残余力，为新得到的质点位置坐标，为当前质点位置坐标，α为缩放因子，记录时间间隔δ中的每个质点的初始位置、最终位置、内力

步骤4.1：建立目标函数

使用前述数据进行监督学习，有：

其中，hθ(η)表示前述准静态方程求解得到的质点的最终位置，η表示自变量θ0，θ1，θ2为三个待定的参数，表示质点的初始位置，表示内力表示重力

步骤4.2：最小二乘法

最小化的损失函数为：

其中，minθj(θ)表示最小化的损失函数，θ表示系数θ0，θ1，θ2向量化构成的向量，η⁽ⁱ⁾与y⁽ⁱ⁾分别表示第i个样本中的变量与质点的最终位置；

步骤4.3：梯度下降算法

上述步骤4.2的第i个梯度分量为：

其中，表示对系数构成的向量θ中的第i个分量求偏导数，ηi表示变量矩阵中的第i个分量；

batch梯度下降算法伪代码：

循环变量i从0到n：

其中，θi表示第i个θ，即θ0，θ1与θ2，n为特征数(变量个数)，β为步长；

设置全局的表示是否学习的布尔变量，得到目标函数的最优参数后，将该布尔变量标记为true，此后，每次受力时，如果已经学习，则直接通过目标函数得到质点受力的最终位置；如果尚未学习，则通过准静态方法求解得到质点的最终位置完成变形；

所述步骤4.1的方程可写作：

其中，θ表示系数θ0，θ1，θ2向量化构成的向量，表示变量向量化构成的向量，t表示转置；

所述图的广度优先搜索算法具体为：以图中的某个顶点为控制点v0出发，访问v0后对与v0邻接的未曾被访问过的顶点w1，w2，...，wk逐次进行访问，然后依次从w1，w2，...，wk出发访问其各自未被访问过的邻接点，如此反复直到图中所有的点都被访问过；控制点所在的三角面片称为碰撞面；

(1)若控制点在某个三角面片的内部，则逐次访问碰撞面的三个顶点后从这三个顶点开始向外搜索；

(2)若控制点在网格结构的某条边上，则从包含该边的所有三角面片的顶点开始逐次向外搜索；

在网格的顶点结构和面结构中设置布尔类型的访问标志初始化为false，表示已访问与否；

将与碰撞点相关的三角形顶点加入队列，并将顶点和碰撞面的访问标志赋值为true，这些数据都是需要复制的数据；

依次从队列中取出头部数据，并计算得到所有通过该顶点的三角面片，如果三角面片的到达标志位false，将其访问标志赋值为true后判断该三角面片是否满足设定的范围条件(是否在受力范围中)；若满足则将该三角面片的所有尚未到达的顶点加入队列尾部，并将访问标志赋值为true；如此循环直到队列为空。

有益效果：本发明所述的一种软组织监督变形算法，与现有技术相比，具有以下优点：

1.本发明提供的方法中的求解状态方程步骤与机器学习相结合，通过构造目标函数，得到最优参数，以带入目标函数的形式代替循环求解，大大减少了计算量。

2.本发明使用了最小二乘法以及梯度下降算法，得到最小化的损失函数和模型参数值，提高了精确度。

3.本发明通过二次数据搜索、细化网格，提高了软组织变形的真实度，提高了精度；该方法提出的软组织变形方法具有较强的鲁棒性，适用于绝大多数虚拟手术。

附图说明

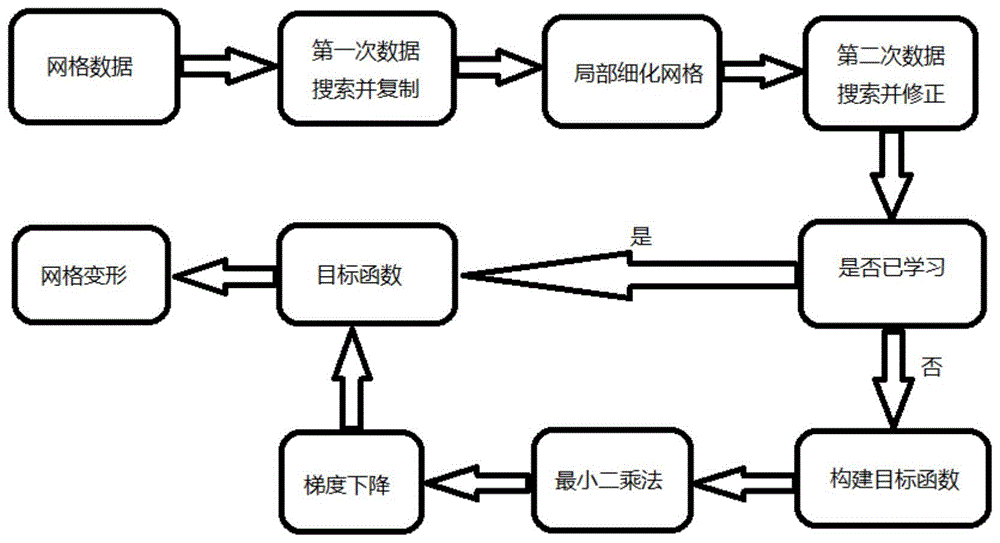
图1为软组织监督变形算法流程图；

图2为图的广度优先搜索图；

图3为最长边平分法图。

具体实施方式

下面结合附图，进一步阐明本发明。

实施例1

如图1-3所示的一种软组织监督变形算法，具体包括如下步骤：

第一步：第一次数据检索并复制，采用广度优先搜索算法采集软组织的数据信息，并基于弹簧质点模型建立软组织的物理模型；

即以图中的某个顶点为控制点v0出发，访问v0后对与v0邻接的未曾被访问过的顶点w1，w2，...，wk逐次进行访问，然后依次从w1，w2，...，wk出发访问其各自未被访问过的邻接点，如此反复直到图中所有的点都被访问过；控制点所在的三角面片称为碰撞面，

(1)若控制点在某个三角面片的内部，则逐次访问碰撞面的三个顶点后从这三个顶点开始向外搜索；

(2)若控制点在网格结构的某条边上，则从包含该边的所有三角面片的顶点开始逐次向外搜索；

在网格的顶点结构和面结构中设置布尔类型的访问标志初始化为false，表示已访问与否；

将与碰撞点相关的三角形顶点加入队列，并将顶点和碰撞面的访问标志赋值为true，这些数据都是需要复制的数据；

依次从队列中取出头部数据，并计算得到所有通过该顶点的三角面片，如果三角面片的到达标志位false，将其访问标志赋值为true后判断该三角面片是否满足设定的范围条件(是否在受力范围中)；若满足则将该三角面片的所有尚未到达的顶点加入队列尾部，并将访问标志赋值为true；如此循环直到队列为空；

第二步：局部细化网格，采用全局最长边平分法对物理模型进行网格细化，找出网格数据中的所有边，判断每条边是否满足平分条件，将所有需要被平分的边加入集合s，对s中的边按照长度的大小进行排序，依次取出s中最长的边并在其中点处插入新的节点，同时按照插入点剖分相应的三角面片，循环计算直到s为空，每次剖分结束后均需要判断新生成的边是否满足剖分条件，若满足则按照长度大小插入s中，保持s有序；需要剖分的边满足条件为：

其中，qij为连接知的边的长度，f函数为网格节点密度需要满足的条件，为质点i的空间坐标，为质点j的空间坐标；

第三步：第二次数据搜索并修正，对细化后的网格进行第二次搜索，将细化后位于物理模型外部的网格数据剔除；

第四步：网格变形，依据步骤三所述的物理模型，对其中的各个质点进行初始化，构建模型的初始状态，该模型中每个质点ni与相连质点nj间的内力为：

其中，是质点ni与质点nj之间的内力，kij是连接质点ni和质点nj的弹簧的弹性系数，是弹簧当前长度减弹簧不受力时的静止长度，其中lij表示弹簧当前长度，表示连接质点ni和质点nj的弹簧不受力时的静止长度，是从质点ni指向质点nj的单位向量；

其中，l′ij为调整后的弹簧长度，参数b用来调控kij随弹簧长度变化而变化的速度，lij为弹簧当前长度，lmin为网格中长度最小的边，lmax为弹簧中长度最大的边，e为弹簧的弹性模量，参数d用来避免长度接近lmin的边的弹性系数过大；

包含n个质点的弹簧质点模型在任意时刻t包含n个偏微分方程，每个方程描述一个质点的运动状态：

其中，mi是质点ni的质量，是质点ni的加速度矢量，ci是质点ni的阻尼系数，是质点ni的速度矢量，σ(i)代表系统中所有与ni邻接的质点的符号，是质点ni的空间坐标，是质点nj的空间坐标，是该质点ni受到的重力，是重力加速度矢量，是作用在ni上的所有外力的矢量和；

弹簧质点模型采用准静态仿真方法计算，

其中，与分别表示质点ni与质点nj的位置；

设s为所有非控制点的符号集合，δ为常数时间间隔，在每个时刻t＝kδ，k＝1，2，...，通过准静态方程求得所有非控制点的位置信息，在时间间隔δ内，重复下述步骤(1)、(2)，实现网格变形：

获得所有控制点的数据信息，对每个i∈s，有：

其中，为每个节点上的残余力，为新得到的质点位置坐标，为当前质点位置坐标，α为缩放因子，记录时间间隔δ中的每个质点的初始位置、最终位置、内力

步骤4.1：建立目标函数

使用前述数据进行监督学习，有：

其中，hθ(η)表示前述准静态方程求解得到的质点的最终位置，η表示自变量θ0，θ1，θ2为三个待定的参数，表示质点的初始位置，表示内力表示重力

步骤4.2：最小二乘法

最小化的损失函数为：

其中，minθj(θ)表示最小化的损失函数，θ表示系数θ0，θ1，θ2向量化构成的向量，hθ等同于h，下标θ表示待优化的系数，η⁽ⁱ⁾与y⁽ⁱ⁾分别表示第i个样本中的变量与质点的最终位置；

步骤4.3：梯度下降算法

上述步骤4.2的第i个梯度分量为：

其中，表示对系数构成的向量θ中的第i个分量求偏导数，ηi表示变量矩阵中的第i个分量；

batch梯度下降算法伪代码：

循环变量i从0到n：

其中，θi表示第i个θ，即θ0，θ1与θ2，n为特征数(变量个数)，β为步长；

设置全局的表示是否学习的布尔变量，得到目标函数的最优参数后，将该布尔变量标记为true，此后，每次受力时，如果已经学习，则直接通过目标函数得到质点受力的最终位置；如果尚未学习，则通过准静态方法求解得到质点的最终位置完成变形。