原位倾斜煤层主渗透率张量卸瓦斯压力响应行为表征方法与流程

本发明属于煤层渗透率定量表征技术领域，具体涉及一种定量表征原位倾斜煤层主渗透率张量在卸瓦斯压力过程中响应行为的方法。

背景技术：

煤层渗透率是影响瓦斯抽采的重要影响因素，其准确表征将影响瓦斯抽采效果，进而影响煤与瓦斯突出预防和矿井安全生产。煤层裂隙网络通常由多组开度、密度、连通性等性质各异的裂隙组成，导致煤渗透率具有各向异性。数学层面上，煤渗透率各向异性可由主渗透率张量表征。主渗透率张量是对角张量，其三个对角线元素即为主渗透率。煤层气开采和瓦斯抽采是卸瓦斯压力过程，此过程中原位煤层处于单轴应变边界条件中，即在卸瓦斯压力过程中上覆岩层产生恒定的竖直应力，煤层在水平方向无变形。现有的数学模型或方法在描述煤层主渗透率卸瓦斯压力响应行为时通常假设主渗透率方向与边界条件正交。对于原位水平煤层，主渗透率方向为水平和垂直方向，此时这种描述方法和可行的。但对于原位倾斜煤层，主渗透率方向不再是水平或垂直的，此时这种描述方法就不可行了，需要寻找新的定量表征原位倾斜煤层主渗透率再卸瓦斯压力过程中响应行为的方法。

技术实现要素：

本发明的目的在于定量表征原位倾斜煤层主渗透率再卸瓦斯压力过程中的响应行为。

为实现上述目的，本发明采用的技术方案如下：

由上述本发明提供的技术方案可以看出，本发明实施方式提供的原位倾斜煤层主渗透率张量卸瓦斯压力响应行为定量表征方法，由于考虑了煤层倾角和节理俯仰角对有效应力对主渗透率响应行为的影响，提高了煤层主渗透率张量预测的精度。

附图说明

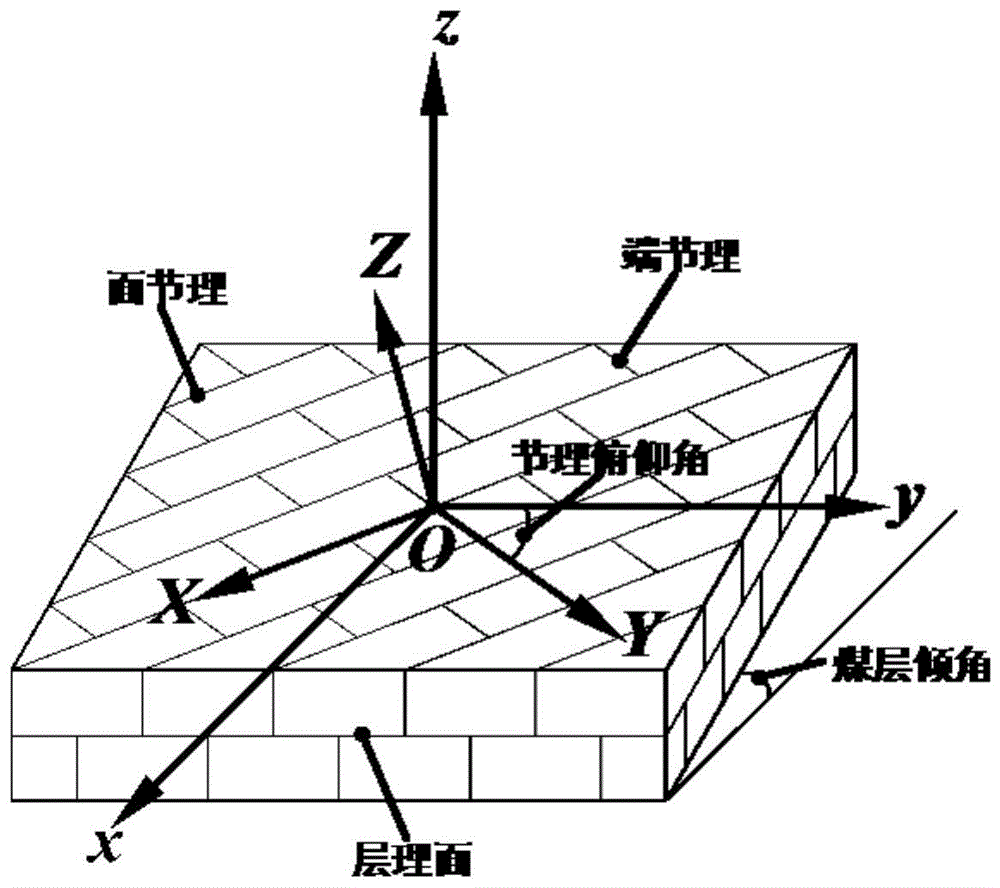
图1是节理坐标系和单轴应变坐标系示意图，图中小写字母x、y和z表示单轴应变坐标系的坐标轴，大写字母x、y和z表示节理坐标系的坐标轴。

图2是单轴应标坐标系旋转过程示意图，图中左侧第一个小图是两个坐标系未旋转时的情形；中间的小图是单轴应变坐标系绕y轴逆时针旋转后的情形；右侧第一个小图是单轴应变坐标系进一步绕z轴旋转后的情形。

具体实施方式

下面结合附图对本发明的实施方式作进一步描述

本实施方案是在如下假设的基础上提出的：

(1)煤层倾斜且平整；

(2)煤层位于单轴应变边界条件内；

(3)煤层包含三组互相正交的节理，即面节理、端节理和层理面。

由于面节理、端节理和层理面互相正交，可以据此构建一个直角坐标系，这个坐标系称为‘节理坐标系’，如图1所示。位于节理坐标系中的各物理量用大写字母‘x’，‘y’和‘z’进行标注。在节理坐标系中，x轴和面节理与层理面的交线平行，y轴和端节理与层理面的交线平行，z轴和面节理与端节理的交线平行。

单轴应变边界条件假设上覆岩层产生恒定的竖直应力，煤层在水平方向无变形。根据此条件构建另一个直角坐标系，称为‘单轴坐标系’，如图1所示。直角坐标系中的物理量用小写字母‘x’、‘y’和‘z’进行标注。在单轴坐标系中，x轴与煤层倾向线在水平面上的投影平行，y轴与煤层的走向线平行，z轴与竖直方向平行。

节理坐标系和单轴坐标系的空间关系可以由两个结构地质学中的参数进行联系：一个是煤层的倾角，另一个是节理的俯仰角。在图2中，煤层的倾角即为煤层层理面(节理坐标系中的oxy平面)和水平面(单轴坐标系中的oxy平面)的锐夹角。节理的俯仰角是端节理平面与煤层走向线或面节理平面与煤层倾向线之间的锐夹角。需要说明的是，煤层倾角(以下简称‘倾角’)和节理俯仰角(一下简称‘俯仰角’)的变化范围是0°到90°。

煤渗透率的卸瓦斯压力响应行为受多种因素影响，如节理孔隙率、弹性参数、吸附参数和有效应力。这些参数中有一些也是各向异性参数因此需要用张量表示。由于张量的表达式取决于与其共轴的坐标系，因此各各向异性参数的张量在节理坐标系中和单轴坐标系中具有不同的表达式。表1列举了各个各向异性参上的张量在两个坐标系中的表达式。煤层参数的张量，如渗透率、节理孔隙率、弹性模量、langmuir吸附常数，在节理坐标系中是只有三个对角线元素的主张量。这些参数在单轴坐标系中的张量有六个元素，其中三个对角线元素和三个非对角线元素。有效应力在节理坐标系和单轴坐标系中的张量均具有六个元素。

表1煤渗透率的卸瓦斯压力响应行为的各向异性影响参数在节理坐标系和单轴坐标系中的张量表达式

表1中，kc是节理坐标系中的渗透率张量；kx、ky和kz是节理坐标系中的正渗透率，即主渗透率；ku是单轴坐标系中的渗透率张量；kxx、kyy和kzz单轴坐标系中的正渗透率；kxy、kyz和kzx是单轴坐标系中的偏渗透率；φac是节理坐标系中的节理孔隙率张量；φax、φay和φaz是节理坐标系中的正节理孔隙率；φau是单轴坐标系中的节理孔隙率张量；φaxx、φayy和φazz是单轴坐标系中的正节理孔隙率；φaxy、φayz和φazx是单轴坐标系中的偏节理孔隙率；ec是节理坐标系中的弹性模量张量；ex、ey和ez是节理坐标系中的正弹性模量；eu是单轴坐标系中的弹性模量张量；exx、eyy和ezz是单轴坐标系中的正弹性模量；exy、eyz和ezx是单轴坐标系中的偏弹性模量；εlc是节理坐标系中的langmuir吸附变形常数张量；εlx、εly和εlz是节理坐标系中的正langmuir吸附变形常数；εlu是单轴坐标系中的langmuir吸附变形常数张量；εlxx、εlyy和εlzz是单轴坐标系中的正langmuir吸附变形常数；εlxy、εlyz和εlzx是单轴坐标系中的偏langmuir吸附变形常数；plc是节理坐标系中的langmuir吸附压力常数张量；plx、ply和plz是节理坐标系中的正langmuir吸附压力常数；plu是单轴坐标系中的langmuir吸附压力常数张量；plxx、plyy和plzz是单轴坐标系中的正langmuir吸附压力常数；plxy、plyz和plzx是单轴坐标系中的偏langmuir吸附压力常数；δσc是节理坐标系中的有效应力张量；δσexx、δσeyy和δσezz是节理坐标系中的正有效应力；δσexy、δσeyz和δσezx是节理坐标系中的偏有效应力；δσu是单轴坐标系中的有效应力张量；δσexx、δσeyy和δσezz是单轴坐标系中的正有效应力；δσexy、δσeyz和δσezx是单轴坐标系中的偏有效应力。

各个各向异性参数在两个坐标系中的张量可以通过坐标旋转进行转换，例如保持节理坐标系不变，单轴坐标系经两步旋转即可与单轴坐标系重合，如图2所示。

第一步是将单轴坐标系绕y轴逆时针旋转与煤层倾角相同的角度。此旋转将产生一个旋转矩阵，如式(1)所示。经过此步旋转，单轴坐标系的x轴位于节理坐标系的oxy平面内，且单轴坐标系的z轴与节理坐标系的z轴重合。

式中，ry是绕单轴坐标系的y轴旋转产生的旋转矩阵；θd是倾角。

旋转矩阵ry是正交矩阵，即其逆矩阵与转置矩阵相同，如式(2)所示。

式中，上标‘-1’表示逆矩阵；上标‘t’表示转置矩阵。

某个各向异性参数a在单轴坐标旋转前和旋转后的张量的关系可由ry和(ry)^t表示，如式(3)所示。

au＝ryai(ry)^-1＝ryai(ry)^t(3)

式中，au表示某个各向异性参数在单轴坐标系旋转前的张量；ai表示该各向异性参数在单轴坐标系旋转后的张量。

第二部是将单轴坐标系绕z轴顺时针旋转与俯仰角相同的角度。此步的旋转矩阵如式(4)所示。经此步旋转后，单轴坐标系与节理坐标系完全重合。

式中，rz是绕单轴坐标系z轴旋转产生的旋转矩阵；θp是俯仰角。

旋转矩阵rz也是正交矩阵，即其逆矩阵与转置矩阵相同，如式(5)所示。

经此步旋转后，各向异性参数的矩阵ai和其在节理坐标系中的矩阵ac的关系可由式(6)表示

ai＝rzac(rz)^-1＝rzrc(rz)^t(6)

将式(6)代入式(3)得

au＝ry[rzac(rz)^t](ry)^t(7)

式(7)还可以写成另外一种形式，如式(8)所示

ac＝(rz)^t[(ry)^taury]rz(8)

假设煤层的弹性模量是各向同性的，节理坐标系中的主渗透率可由式(9)表示

式中，fin是内膨胀应变系数；p是瓦斯压力；p0是初始瓦斯压力。

式(9)δσexx、δσeyy和δσezz是未知量，需要重新推导。将节理坐标系中的有效应力张量δσc和单轴坐标系中的有效应力张量δσu代入式(8)的

δσc＝(rz)^t[(ry)^tδσury]rz(10)

将式(1)、(2)、(2.4)和(5)代入式(10)可以得到两个坐标系中正应力之间的关系，如式(11)所示

单轴坐标系中的正有效应力δσexx,δσeyy,andδσezz可由式(12)表示

式(12)中，exx、eyy和ezz是未知量，需要重新推导。将节理坐标系中的弹性模量张量ec和单轴坐标系中的弹性模量eg代入式(7)得

eg＝ry[rzec(rz)^t](ry)^t(13)

将式(1)、(2)、(4)和(5)代入式(13)可以得到单轴坐标系中的正弹性模量exx、eyy和ezz与节理坐标系中正弹性模量ex、ey和ez之间的关系，如式(14)所示。

将煤层假设为横观各向同性材料，且层理面为各向同性面，则与层理面平行方向各向同性，层理面平行方向与垂直方向各向异性。此时ex与ey相等，则式(14)退化为式(15)。

将式(15)代入式(12)得

综合式(9)、(11)和(16)即可得到在单轴应变条件下原位倾斜煤层主渗透率卸瓦斯压力响应行为的完整表达式，如式(17)所示。