一种在耦合振子系统中实现非对称振荡死亡的方法与流程

本发明属于非线性动力学中振荡死亡控制技术领域，通过在扩散耦合振子系统中引入有源低通滤波器，对反馈耦合作用的信号进行滤波后再进行放大。在有源滤波器的作用下，在耦合振子系统中实现非对称振荡死亡态的方法。

背景技术：

近年来，耦合振子系统的集体动力学行为在物理、生物和工程领域都引起了强烈的关注。斑图的形成和自组织行为的出现与各种各样的同步和振荡淬灭现象密切相关，其中振荡淬灭主要包括振幅死亡(ad)和振荡死亡(od)，振幅死亡是由于系统中的两个或两个以上的振子间的耦合作用使得振荡受到抑制从而趋于一种零振幅的稳定状态，振荡死亡是由于振子系统的对称性破缺，均匀的稳定态发生分裂形成两个分支，最终振子系统处于不同的不均匀稳定状态。在电子电路和生物学等实际应用中，耦合系统的振幅死亡和振荡死亡动力学已经被广泛研究。近些年来，研究人员开始关注从振幅死亡到振荡死亡转换的动力学机制并取得大量成果，其中koseska等人观察到在非全同耦合振子中，振幅死亡能通过超临界叉形分岔过渡到振荡死亡。后来邹为等人发现在具有时延耦合的全同金兹堡－朗道振子系统中也可以出现从振幅死亡到振荡死亡的转换。与此同时，在许多生物系统的相变过程中出现了多稳态的特征，另外还观察到一种新的振荡淬灭状态为非普通振幅死亡(ntad)，与振幅死亡(ad)相比ntad是一种振幅不为零的均匀稳定状态。

在实际耦合系统尤其是电子电路系统和生物系统中，相互作用的耦合项与低通滤波电路的特性一样可能会改变输入信号的振幅和相位，并且低通滤波器(lpf)的这种特性广泛应用在人体肌肉骨骼系统、小龙虾的腹部神经节、锁相环模块、通信信道和混沌控制等领域。低通滤波器在一定程度上可以改变耦合振子系统的动力学行为，而且有可能最终使耦合系统产生振荡死亡。目前较常见的报道是滤波器作用下可以使耦合振子系统产生振幅死亡和对称的振荡死亡现象。而对于耦合作用下能否产生非对称的振荡死亡尚不明确。因耦合振子处于非对称振荡死亡时，两个振子处于不相等，也不对称的两个稳定态，此固定点更具有普遍性。

技术实现要素：

1、发明目的

为了在耦合振子系统获得稳定的非对称振荡死亡态，本发明拟通过在耦合振子系统中引入有源滤波器的作用。通过有源滤波器中具有放大特性的有源器件，使耦合系统原有不稳定的非对称固定点变成稳定固定点而获得稳定的不对称振荡死亡现象。

2、技术方案

一种在耦合振子系统中实现非对称振荡死亡的方法，包括以下步骤:

第一步：在扩散耦合振子系统(以两个耦合金兹堡－朗道振子为例)中，对耦合输入信号利用有源低通滤波器进行滤波，然后再进行反馈耦合，得到耦合系统：

(1)式中状态变量zi＝xi+jyi，j为纯虚数。re(zi)是耦合系统的实部，ω是振子的固有频率，ε是耦合强度，α是滤波器截止频率，q表示有源低通滤波器的放大系数，当1<q≤2时滤波器对其输入信号有放大作用，si表示以re(zi)作为输入信号后，有源低通滤波器的输出信号。

第二步：对(1)系统的固定点稳态值进行求解，令方程(1)式的左边等于零，可以计算出方程(1)对应的所有固定点，并写成一般形式的表达式：γ(x^m,y^m,σx^m,σy^m,x^m,σx^m)。其中，当{x^m＝0,y^m＝0}时表示固定点o(0,0,0,0,0,0),若该固定点变成稳定，则耦合系统会到达振幅死亡态(ad),即耦合系统最后走向相等的两个为零的固定点。当{m＝*,σ＝-1}时，固定点为γihss＝(x^*,y^*,-x^*,-y^*,x^*,-x^*)，该固定点变成稳定时，耦合系统处于对称振荡死亡态(sod)，即两个耦合振子处于关于原点对称的两个固定点上。当{m＝+,σ＝1}时，固定点为当该固定点变成稳定时，耦合系统为非普通的振幅死亡态(ntad)，即耦合振子系统处于相等且不为零的固定点上。当{x^m＝x1,y^m＝y1,σx^m＝x2,σy^m＝y2}时，固定点为γasod＝(x1,y1,x2,y2,x1,x2)，当该固定点变稳定时，耦合振子系统处于非对称固定点态(asod),即两个耦合振子处于不相等的两个固定点上。其中各个变量的值可表示为(2-4)式。

注意到(2-4)式中的固定点的存在性与滤波器截止频率α无关，而与有源滤波器的有源器件的放大或衰减系数q有关。

第三步：对(2-4)固定点解进行线性稳定性分析，可以确定耦合系统实现相应的稳态解所需的参数区间。具体地，固定点的稳定性可由其线性化矩阵的特征值的最大实部re(λmax)来确定，即re(λmax)<0是固定点的稳定性条件。通过对固定点做线性稳定性分析得到其线性化矩阵(即雅克比矩阵)为

其中，a11＝(1-3(x^m)²-(y^m)²-ε),a12＝(-ω-2x^my^m),a21＝(ω-2x^my^m),a22＝(1-(x^m)²-3(y^m)²),b11＝εq。

第四步：计算各固定点的线性化矩阵的特征值，并确定所有使最大特征值实部小于零的参数区域。从而确定各种固定点的稳定参数区域。

第五步：通过xppaut软件可进一步观察不同参数对耦合振子系统固定点稳定性的影响情况。

3.有益效果：

本发明将耦合振子系统的输入信号通过有源低通滤波器(截止频率α)进行滤波，有源器件的存在会对滤波器输出信号进行放大(1<q≤2)，放大后的信号再反馈回耦合项。通过选择合适的放大系数，耦合振子系统的自然频率参数和耦合强度，可以在耦合振子系统中实现非对称振荡死亡态。在实际耦合系统中，尤其是电子电路和生物网络中，具有有源低通滤波器特性的耦合作用项是普遍存在的，因此该方法的相关理论具有理论指导意义，同时具有潜在的实用价值。

附图说明

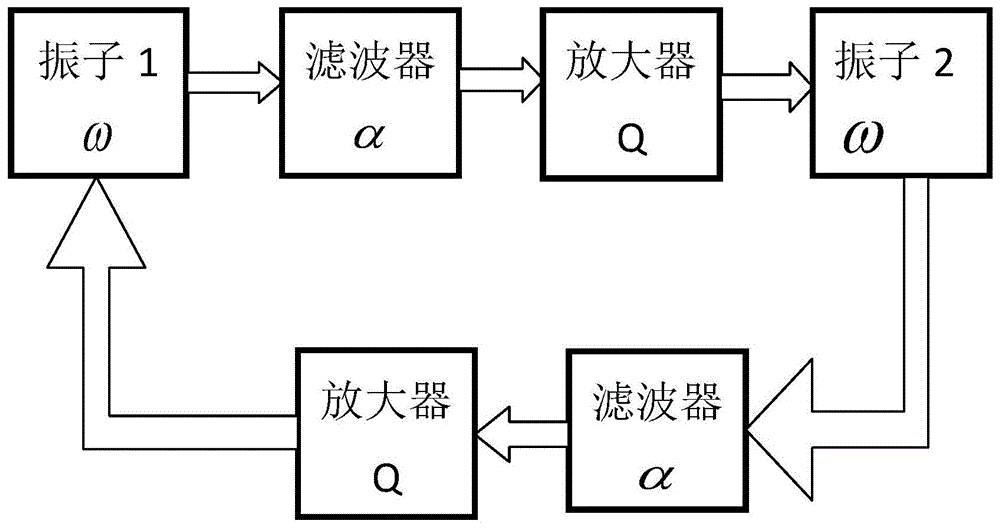
图1为具有有源器件的低通滤波器耦合控制系统的原理框图。

图2(a)-(c)分别为两个全同扩散耦合金兹堡－朗道振子系统中,滤波器截止频率为α＝8,3,1且q为放大系数(q＝1.2)时在ω-ε参数空间的状态区域图。其中i区域为振幅死亡(ad)，ii区域为对称振荡死亡(sod)，iii区域为振荡态(os)，iv区域为非普通振幅死亡(ntad)，v区域为振荡态与对称振荡死亡共存区，vi区域为非普通振幅死亡与振荡态共存区，vii区域为非对称振荡死亡与振荡态共存区。(d)-(f)分别为与图2(a)-(c)图对应参数下，且ε＝8.0时变量x1随参数ω的分岔图。

图3(a)-(f)为两个全同扩散耦合金兹堡－朗道振子系统中,有源滤波器参数截止频率α＝1，且放大系数q＝1.2,耦合强度参数ε＝8.0时的时序图。(a)ω＝0.5时，非普通振幅死亡，(b)ω＝1.39对称振荡态与非对称振荡态共存时序图，(c)ω＝1.5对称振荡态与非对称振荡死亡态共存，(d)ω＝3.0对称振荡态与对称振荡死亡态共存，(e)ω＝3.8对称振荡死亡态，(f)ω＝6.0振幅死亡态。

图4(a)-(c)为n＝4个金兹堡－朗道振子全局耦合时，有源低通滤波器的截止频率分别为α＝8,3,1，且放大系数q＝1.2时在ω-ε参数空间的状态区域图。其中i区域为振幅死亡区，iii区域为振荡态区，iv区域为非普通振幅死亡区，v区域为对称振荡死亡和振荡态共存区域，vi区域为非普通振幅死亡和振荡态共存区，vii区域为非对称振荡死亡与振荡态共存区域。(d)-(f)分别为与图3(a)-(c)图对应参数下，且ε＝10.0时变量x1随参数ω的分岔图。

具体实施方式

下面结合实施实例和附图对本发明作进一步说明。

实施例1：两个振子耦合系统

对于形如图1所示系统模型，其表达式可以写成公式(1)，其有固定点解γ(x^m,y^m,σx^m,σy^m,x^m,σx^m)，通过对该固定点做线性化稳定性分析，得到线性化矩阵式(5)，并可计算出其特征方程满足式(λ³+p2λ²+p1λ+p0)(λ³+p2'λ²+p1'λ+p0')＝0,(6)

其中，

p2＝-2+4(r^m)²+ε+α,

p1＝1+α[4(r^m)²-2+ε(1-q)]+ω²+3(r^m)⁴-4(r^m)²-ε(1-(r^m)²-2(y^m)²),

p0＝α[1-4(r^m)²+3(r^m)⁴+ω²-ε(1-q)(1-(r^m)²-2(y^m)²)],

p2'＝-2+4(r^m)²+ε+α,

p1'＝1+α[4(r^m)²-2+ε(1+q)]+ω²+3(r^m)⁴-4(r^m)²-ε(1-(r^m)²-2(y^m)²),

p0'＝α[1-4(r^m)²+3(r^m)⁴+ω²-ε(1+q)(¹-(r^m)²-2(y^m)²)],

(r^m)²＝(x^m)²+(y^m)²(7)

由(6)式，分别代入不同的固定点，并计算该固定点下所有特征值实部小于零的参数空间。可得到相应固定点的稳定区域。如图2(a)-(c)分别给出了放大系数q＝1.2时，不同滤波器参数截止频率α＝8,3,1时对应的不同稳定态的参数区域。当α＝8时，在自然频率和耦合强度参数区间，有四个稳态区域，它们为振幅死亡区间(i区域)，振荡态区间(iii区域)，非普通振幅死亡区间(区域iv)，对称振荡死亡与振荡态共存区间(区域v)。当减小低通滤波器的截止频率，使α＝1时，振幅死亡区间(i区域)增加，振荡区间(iii区域)减小，对称振荡死亡与振荡共存区域(v区域)减少，并产生对称振荡死亡区(ii区域)和非对称振荡死亡态(与振荡态共存)(vii区域)。

进一步通过xppauto软件，分别作耦合系统在与图2(a)-(c)对应的参数α，且耦合强度参数ε＝8时，变量x1随参数ω变化的分岔图。图2(a)中，随着参数ω减少，耦合振子系统会从振幅死亡(ad)态通过霍普夫分岔而失稳，然后再经叉型分岔后走向不稳定对称固定点，然后不稳定固定点变成稳定的固定点形成对称振荡死亡态(sod)。此时，通过霍普夫分岔产生的对称振荡态一直保持稳定，直到出现非普通振幅死亡后消失。从而产生振荡态与对称振荡死亡共存区。注意到当参数α＝1时，随着参数ω减少，振幅死亡通过叉型分岔产生稳定的对称振荡死亡态，然后稳定对称振荡死亡态再经第二次叉型分岔产生非对称振荡死亡态。最后非对称耦振荡死亡态经第二次霍普夫分岔产生非对称振荡态。这个分岔过程与霍普夫分岔产生的振荡态共存。

实施例2：四个全局耦合振子系统

在n＝4个全局耦合振子系统(以金兹堡－朗道方程为例)中，耦合振子两两之间均具有相互作用，且对每个振子的信号均通过有源低通滤波器进行滤波，然后再将滤波后的信号经有源放大器后反馈耦合到其它振子中。耦合振子系统的模型可写为：

(8)式中zi＝xi+jyi，j为纯虚数。re(zi)是耦合系统的实部，ω是振子的固有频率，ε是耦合强度，α是滤波器的截止频率，q表示有源低通滤波器的放大系数，当1<q≤2时滤波器对其输入信号有放大作用。si表示以作为输入信号后，有源低通滤波器的输出信号。

对公式(8)所述系统的控制目标稳态值进行求解，令公式(8)的左边等于零，可以得到均匀稳定状态(hss)固定点为o(0,0,0,0,0,0,0,0,0,0,0,0)，非均匀稳定状态(ihss)固定点为非普通均匀稳定状(nhss)固定点和非对称振荡死亡(asod)固定点以上各固定点中的值可以表示为式(9)-(11)。

通过对所有固定点做线性化稳定性分析，得到线性化矩阵式(12)，并可计算出其特征方程满足式(13),

其中，

a＝1-3x^m2-y^m2-ε,b＝-ω-2x^m2y^m2,c＝ω-2x^m2y^m2,d＝1-x^m2-3y^m2(λ⁶+p5λ⁵+p4λ⁴+p0)(λ³+p2λ²+p1λ+p0′)＝0(13)

其中，

由(12)式求解出特征值，当所有特征值实部均小于零时对应的固定点为稳定固定点。由此可得到各种固定点的稳定参数区间。如图4(a)-(c)分别给出了放大系数q＝1.2时，不同滤波器参数截止频率α＝8,3,1时对应的不同稳定态的参数区域。当α＝8时，在自然频率和耦合强度参数区间，有四个稳态区域，它们为振幅死亡区间(i区域)，振荡态区间(iii区域)，非普通振幅死亡区间(iv区域)。当α＝1时，振幅死亡区间(i区域)增加，振荡区间(iii)减小，对称振荡死亡与振荡态共存区间(v区域)减少，并产生非普通振幅死亡与振荡态共存区间(vi区域)，和非对称振荡死亡与振荡态共存区域(vii区域)。

利用xppaupto软件可得到各稳定态随参数变化的分岔图，从而可以确定各种形式的稳定态随参数的变化。如低通滤波器截止频率α和滤波器输出信号的放大系数q对相变过程的影响。在放大系数1<q<2的情况下，如图4(d)-(f)可知滤波器的引入使得在全局扩散耦合振子中出现了从对称振荡死亡(od)到非对称振荡死亡(asod)再到非对称振荡(asos)的相变转换过程。并且这个相变过程与同步振荡是共存的，随着滤波作用的增强，ad区域和od、os的共存区增大,并产生非对称振荡死亡态(asod)。