一种基于电热耦合的全钒液流电池储能系统等效方法与流程

本发明涉及电力系统电池建模
技术领域：
，具体地指一种基于电热耦合的全钒液流电池储能系统等效方法，提出了一种适合于电网储能系统仿真的电气等效模型。
背景技术：
：随着环境污染和能源危机的加剧，应用太阳能、风能、水能等可再生能源发电尤为重要。但是可再生能源自身所固有的随机性、间歇性特征，严重阻碍了电网系统安全和经济的运行。而储能系统的可调度性，能够有效的改善新能源发电的不稳定所造成的问题。全钒液流电池因其具有容量大、循环寿命长、环境友好、功率与容量可独立设计等特征，成为电力系统大规模储能的首选技术之一。电解液温度的变化对液流电池内部化学反应造成影响。温度控制不当会导致反应物沉淀，甚至堵塞流道，影响电池的安全高效运行。然而，现有电气等效模型未考虑温度对液流电池外特性的影响。在目前的研究中，专利《一种全钒液流电池储能系统的等效模拟方法》(专利号：201410089721.4)提出了二阶动态等效模型；文献(《全钒液流电池仿真模型综述》)对比分析了不同等效电路模型的基本原理以及各自特点，并提出了常用的一种等效模型；文献(《全钒液流电池储能系统仿真建模及其应用研究》)针对全钒液流电池储能系统建模开展研究，文中假设反应过程中温度维持恒定，未考虑设定温度与实际运行温度相差较大时造成的误差。因此，本发明设计了一种考虑温度影响的电热耦合模型。技术实现要素：本发明的目的是为了解决上述
背景技术：
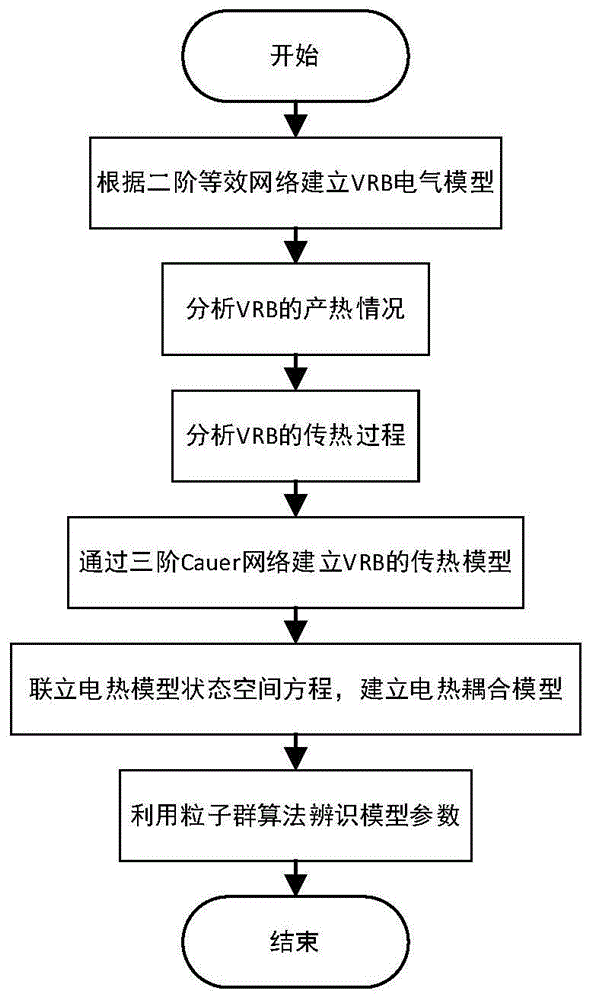
存在的不足，提出一种基于电热耦合的全钒液流电池储能系统等效方法，该方法考虑了温度、漏电流和自放电现象对电池的影响，并对vrb储能系统的产热和传热过程进行动态建模，提出了三阶cauer等效热路网络模型，该技术方法既可以准确反映全钒液流电池系统外特性，又可以作为储能系统系统级仿真的基础。为实现上述目的，本发明所设计的一种基于电热耦合的全钒液流电池储能系统等效方法，其特殊之处在于，所述方法包括如下步骤：步骤1：使用二阶阻容网络对全钒液流电池vrb的电气特性进行建模，并用式(1)—式(6)表示：uter＝eocv-ucon-uact-uohm(1)uohm＝irohm(3)式(1)表示电池端电压的组成，uter为vrb的端电压；式(2)中描述了电池的荷电状态和开路电压的变化规律，其中，soc为电池的荷电状态，即剩余电量；cn表示电池的容量；i(t)为充放电电流，η为充放电效率；soc0为系统初始的荷电状态；eocv为电池电压源，代表了vrb电堆在不同soc下的平衡电动势emf，由能斯特方程导出；e0表示标准电极电位；r表示摩尔气体常数；t表示当前温度；f表示法拉第常数，k1、k2表示为修正soc不准确而添加的修正系数；式(3)中，uohm为欧姆过电势，代表了双极板、薄膜、电解质上的等效压降，rohm表示钒电池的等效内阻，代表了双极板、薄膜、电解质的等效电阻之和，i表示输入电流；式(4)中，uact为活化过电势，在模型中用阻容网络等效表示，ract和cact分别为等效电阻和等效电容，t表示反应进行的时间，用于描述暂态过程；式(5)中，ucon为浓差过电势，在模型中用阻容网络等效表示，rcon和ccon分别为等效电阻和等效电容；式(6)中，rsh//rdiff为自放电损耗电阻与旁路电流损耗电阻，由电解液的导电性与钒电池的流体管道设计决定，σ表示电解液的导电性，l表示电极长度，s表示电极宽度，ra,c表示管道等效电阻；步骤2：依据实验数据，通过粒子群算法，对步骤1中等效电路方程的参数rohm、ract、rcon、cact和ccon进行辨识；步骤3：分析在电池运行中等效电阻产热、化学反应吸/放热、电堆中由传质粘度和摩擦造成的产热三种状态，并采用式(8)—式(11)所示的方程进行描述：pσ＝pr+pentro+pflow(8)式(8)表示电池中各个产热部分的组成，p∑为电池总产热量，pr为各等效电阻产热，pentro表示化学反应吸/放热，pflow为电堆中由传质粘度和摩擦造成的产热；式(9)表示当电流为变量时，各项电阻的产热，等式右侧第一项为自放电和旁路电流的产热，第二项为等效欧姆电阻、活化电阻和浓差电阻的产热，并包含了暂态过程，rshunt、rdiff分别为旁路电流损耗电阻与自放电损耗电阻；式(10)表示化学反应吸/放热，其符号由充放电状态决定，e表示反应熵热；ts为电堆内部电解液的温度；z表示反应中电子转移数，c表示离子浓度；式(11)表示由传质粘度和摩擦造成的产热，q表示管道中传质的流量；δptotal表示传质总的压力降；α为泵的效率，取决于泵的配置和运行条件；μ表示传质的粘度；l和s表示电极的长度和截面积；κ为电极的渗透率；步骤4：基于电热比拟原理，使用cauer等效网络对vrb储能系统的传热路径进行等效；步骤5：将步骤2和步骤4中得到的结果进行联立，得到完整的vrb储能系统电热耦合模型的状态空间方程：uter＝h(x,u)(16)式(15)中，x表示系统中的各个状态量，u表示系统的输入量；a为系统矩阵，b为输入矩阵；式(16)中，uter表示输出端电压。优选地，所述步骤2的具体过程为：步骤201：输入实验得到的电流i、荷电常数soc和对应的端电压uter，在约束条件内，初始化一个含有m个粒子的粒子群，粒子的维度d取5，各维度分别代表[rohmractrconcactccon]的值，并设置约束条件：(i)限制欧姆电阻rohm_min≤rohm≤rohm_max(ii)限制活化电阻ract_min≤ract≤ract_max(iv)限制浓差电阻rcon_min≤rcon≤rcon_max(v)限制活化电容cact_min≤cact≤cact_max(vi)限制浓差电容ccon_min≤ccon≤ccon_max步骤202：将各粒子参数代入式(1)—式(5)，计算出对应的荷电常数soc和端电压uter，与实验结果比较，计算方差，得出每个粒子的适应度值；步骤203：若存在粒子的适应值更优于历史粒子的适应值，则更新粒子的个体历史最佳值pbest与种群历史最佳位置gbest；步骤204：根据式(7)，更新粒子的速度与位置，并对超出约束条件的粒子进行边界处理；式(7)中，k表示其迭代次数；xi表示粒子i的位置向量；vi表示粒子i的速度向量；参数w表示惯性权重；pi表示粒子i的历史最佳位置向量；gi表示粒子群内所有粒子的历史最佳位置向量；c1表示自我学习因子；c2表示群体学习因子；r1和r2为该区间内均匀分布的伪随机数，取值范围为[0,1]；步骤206：输出最终得到的参数。优选地，所述步骤4)中cauer等效网络通过式(12)—式(14)表示：式(12)—式(14)为cauer等效网络的电路方程，t1、t2、t3、tair分别表示vrb系统中电堆、管道、散热器和环境的温度；tair表示vrb系统中电堆、管道、散热器和环境的温度；rth-s、rth-p、rth-he和rth-air分别是电堆、管道、散热器和空气的等效热阻；cth-s为cth-p、cth-he分别是电堆、管道和散热器的等效热容。优选地，所述步骤5)的式(15)中x＝[uactuconsoct1t2t3]t(17)u＝[ipσtair]t(18)最佳地，所述步骤201中的约束条件为：(i)限制欧姆电阻0.03≤rohm≤0.06(ii)限制活化电阻0.001≤ract≤0.03(iv)限制浓差电阻0.0001≤rcon≤0.01(v)限制活化电容10≤cact≤2000(vi)限制浓差电容1000≤ccon≤5000。本发明的优点在于：(1)本发明综合考虑了vrb储能系统在运行时的电气特性和产热特性以及两者间的耦合关系，能够对电池的荷电状态、端电压和各部分温度状态进行准确地预测，有效保障vrb的安全稳定运行。(2)储能系统的工作状态受多种因素影响，本发明使用二阶阻容网络提高电气模型的动态响应能力，能够有效反映功率的动态变化过程对电池的影响。(3)本发明通过三阶cauer网络，对vrb系统复杂的传热过程进行简化，在不影响精度的前提下大大提高了计算速度，有利于对电池温度的及时预测和告警。附图说明图1为本发明提出的一种基于电热耦合的全钒液流电池储能系统等效方法的流程图。图2为全钒液流电池电热耦合关系的等效电路模型图。图3为全钒液流电池传热路径的cauer等效热路网络模型图。图4为本发明提出的一种基于电热耦合的全钒液流电池储能系统等效方法的粒子群算法流程图。图5为粒子群算法辨识后模型仿真与实验数据对比图。具体实施方式以下结合附图和具体实施例对本发明作进一步的详细描述。本发明提出一种基于电热耦合的全钒液流电池储能系统等效方法，包括建立全钒液流电池的数学模型，对全钒液流电池的数学模型进行参数辨识，采用遗传算法对全钒液流电池的瞬时能量效率进行实时优化，得到不同soc下运行时的最高瞬时能量效率，以及该效率对应的流速、温度和电流值。具体实例中以5kw/3.3kwh的全钒液流电池为例进行描述，全钒液流电池的参数如表1所示。表1全钒液流电池的参数参数名称/单位数值功率/kw5容量/kwh3.3安时容量/ah62额定电压/v48额定电流/a105放电限压/v40充电限压/v60如图1所示，本发明提出的基于电热耦合的全钒液流电池储能系统等效方法按如下步骤进行。步骤1：根据全钒液流电池的等效电路模型建立全钒液流电池的数学模型，并采用式(1)—式(6)对所示的方程对数学模型进行表示：uter＝eocv-ucon-uact-uohm(1)uohm＝irohm(3)式(1)表示电池端电压的组成，uter为vrb的端电压。式(2)中描述了电池的荷电状态和开路电压的变化规律，其中，soc为电池的荷电状态，即剩余电量；cn表示电池的容量；i(t)为充放电电流，η为充放电效率；soc0为系统初始的荷电状态；eocv为电池电压源，代表了vrb电堆在不同soc下的平衡电动势emf，由能斯特方程导出；e0表示标准电极电位；r表示摩尔气体常数，本实例为8.314j/(k·mol)；t表示当前温度；z表示反应中电子转移数,取1；f表示法拉第常数,96500c/mol；k1、k2表示为修正soc不准确而添加的修正系数；式(3)中，uohm为欧姆过电势，代表了双极板、薄膜、电解质上的等效压降，rohm表示钒电池的等效内阻，代表了双极板、薄膜、电解质的等效电阻之和，i表示输入电流。t表示反应进行的时间，用于描述暂态过程。式(4)中，uact为活化过电势，在模型中用阻容网络等效表示，ract和cact分别为等效电阻和等效电容。式(5)中，ucon为浓差过电势，在模型中用阻容网络等效表示，rcon和ccon分别为等效电阻和等效电容。式(6)中，rsh//rdiff为自放电损耗电阻与旁路电流损耗电阻，由电解液的导电性与钒电池的流体管道设计决定，σ表示电解液的导电性，l表示电极长度，63cm，s表示电极宽度，75cm，ra,c表示管道等效电阻。步骤2：依据实验数据，通过粒子群算法，对步骤1中等效电路的各个参数进行辨识。具体过程为：步骤201：输入实验得到的电流i，系统荷电常数初值soc0，在约束条件内，初始化一个含有50个粒子的粒子群，粒子的维度d取5，各维度分别代表[rohmractrconcactccon]的值，设置惯性权重w＝1；自我学习因子c1＝1.2；群体学习因子c2＝1.2；设置如下约束条件：(i)限制欧姆电阻0.03≤rohm≤0.06(ii)限制活化电阻0.001≤ract≤0.03(iv)限制浓差电阻0.0001≤rcon≤0.01(v)限制活化电容10≤cact≤2000(vi)限制浓差电容1000≤ccon≤5000在约束条件内赋予每个粒子随机的速度与位置。步骤202：将各粒子参数代入式(1)—式(5)，计算出对应的荷电常数soc和端电压uter，与实验结果比较，得出每个粒子的适应度值。步骤203：若存在粒子的适应值更优于历史粒子的适应值，则更新粒子的个体历史最佳值pbest与种群历史最佳位置gbest。步骤204：根据式(7)，更新粒子的速度与位置，并对超出约束条件的粒子进行边界处理。式(7)中，k表示其迭代次数；xi表示粒子i的位置向量；vi表示粒子i的速度向量；参数w表示惯性权重；pi表示粒子i的历史最佳位置向量；gi表示粒子群内所有粒子的历史最佳位置向量；c1表示自我学习因子；c2表示群体学习因子；r1和r2为该区间内均匀分布的伪随机数，取值范围为[0,1]。步骤205：重复步骤202—204，直到该模型拟合曲线与实验曲线的误差小于指定的数值。步骤206：输出最终得到的参数。rohm(ω)ract(ω)rcon(ω)cact(f)cact(f)rmse0.051380.00640.00421042.550000.128步骤3：分析在电池运行中各个模块的产热情况，并采用式(8)—式(11)所示的方程进行描述：pσ＝pr+pentro+pflow(8)式(8)表示电池中各产热部分的组成，p∑为电池总产热量，pr为各等效电阻产热，pentro表示化学反应吸(放)热，pflow为电堆中由传质粘度和摩擦造成的产热。式(9)表示当电流为变量时，各项电阻的产热，等式右侧第一项为自放电和旁路电流的产热，第二项为等效欧姆电阻、活化电阻和浓差电阻的产热，并包含了暂态过程。rshunt、rdiff分别为旁路电流损耗电阻与自放电损耗电阻，由电解液的导电性与钒电池的流体管道设计决定。式(10)表示化学反应吸(放)热，其符号由充放电状态决定(放电时为正，充电时为负)，e表示反应熵热，可以由能斯特方程推导得到。ts为电堆内部电解液的温度。r表示摩尔气体常数，t表示当前温度，z表示反应中电子转移数，f表示法拉第常数，c表示各种离子的浓度。式(11)表示由传质粘度和摩擦造成的产热，q表示管道中传质的流量；δptotal表示传质总的压力降；α为泵的效率，取决于泵的配置和运行条件；μ表示传质的粘度；l和s表示电极的长度和截面积；κ为电极的渗透率。步骤4：基于电热比拟原理，对vrb储能系统的传热路径进行等效。通过式(12)—式(14)表示：式(12)—式(14)为cauer等效网络的电路方程，与图2中热模型对应。其中t1、t2、t3、tair分别表示vrb系统中电堆、管道、散热器和环境的温度，rth-s、rth-p、rth-he和rth-air是电堆、管道、散热器和空气的等效热阻；cth-s为cth-p、cth-he是电堆、管道和散热器的等效热容。经等效计算得到的参数值：rth-s(ω)rth-p(ω)rth-t(ω)cth-s(f)cth-p(f)cth-t(f)1.3x10-55.1x10-51.1x10-41.3x1065.0x1062.1x106步骤5：将步骤2和步骤4中得到的各个状态进行联立，得到完整的vrb储能系统电热耦合模型的状态空间方程。用式(15)—式(20)表示。uter＝h(x,u)(16)式(15)中，x表示系统中的各个状态量，u表示系统的输入量；a为系统矩阵，b为输入矩阵；式(16)中，uter表示输出端电压。x＝[uactuconsoct1t2t3]t(17)u＝[ipσtair]t(18)本领域的技术人员应当理解，此处所述的具体实施方案仅用解释本发明专利，并不用于限制本发明专利。在本发明专利的精神和原则之内作出的任何修改、等同替换和改进等，均应包含在本发明专利的保护范围之中。当前第1页12