配电网负荷预测中的Lyapunov指数计算方法与流程

本发明涉及一种lyapunov指数计算方法，尤其涉及一种配电网负荷预测中的lyapunov指数计算方法，属于电力负荷预测技术领域。

背景技术：

由于近些年各类新能源发电装置入网及电动汽车的普及，使得配电网负荷的组成愈加复杂，配电网的负荷变化受人口、经济、工业发展水平、气象及政治等多方面因素的影响，因此配电负荷预测具有非线性和不确定性的特点。而混沌系统是一种由确定性系统产生，受初始条件影响较大的介于随机性和确定性之间的系统。

国内外已有部分学者将混沌理论应用于电力负荷预测中以减少凭经验构建单一预测模型的主观性，试图达到更为精确的预测效果。而一个系统的混沌性判断是对系统应用混沌理论预测的前提。lyapunov指数是衡量系统动力学特性的一个重要定量指标,表征了系统在相空间中相邻轨道间收敛或发散的平均指数率，能够有效表达混沌系统对初始值的敏感度。如果某一系统至少存在一个正的lyapunov指数，那么说明这一系统必然为混沌系统，在工程上可以利用lyapunov指数实现对系统混沌性的识别。

系统在某一时刻的状态称为相，所有的系统状态组成相空间。为得到动力系统信息，需要充分了解系统的状态信息，但在工程中，数据采集设备只能得到反映系统信息的一维时间序列向量。相空间重构是根据有限的数据重构吸引子，以研究系统动力行为的方法。基本思想：系统中任一分量的演化都是由与之相互作用的其他分量所决定，相关分量的信息隐含在任一分量的发展过程中，即用系统的一个观察量可以重构出原动力系统模型。一个正的lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。

由于混沌系统对初始状态极为敏感，即使两个在混沌系统中距离很接近的初始点的运动轨迹也会随着时间的推移以lyapunov指数速度分离，lyapunov指数能够表达混沌系统对初始值的敏感度。如果某一系统至少存在一个正的lyapunov指数，那么说明这一系统必然为混沌系统。

目前利用时间序列计算lyapunov指数主要有分析法和轨道跟踪法两类方法，rosenstein法属于轨道跟踪法中的一种。

(1)rosenstein算法：

rosenstein法计算lyapunov指数的计算步骤：

(i)对观测到的以δt为间隔的时间序列{xi},i＝1,2,l,n选择重构维数m和时延t，重构相空间xi＝[xi,xi+t,l,xi+(m-1)t]。

(ii)寻找每一个空间相点xj的最邻近点

(iii)计算其中k为常数。这里的xj+i为xj在相空间中经过i步演化后的相空间点，为经过i步演化后的相点。

(iv)由于这一距离会随时间推移以lyapunov指数速度发散，故其中

(v)对取对数，得lndj(i)≈λ1(iδt)+ln(cj)。对等式两边的j取全局平均，得<lndj(i)>≈λ1(iδt)+<ln(cj)>，其中<l>表示取全局平均。

(vi)令得式中后一项近似为常数，所以此式近似一条以λ1为斜率，i为自变量的直线。

但此方法存在一个缺点：在步骤2中寻找xj的最邻近点时，只寻找与xj距离最近的点。但在工程实际中由于受到噪声的影响，这一点不一定是真实的最邻近点，而有可能是噪点。

(2)kantz算法：

为减小噪声的影响，kantz算法在计算时，给定了一个邻域范围ε，在邻域ε内利用多点平均的方式减小噪声影响。但问题是对于一个确定的邻域ε，可能在xj附近能找到很多邻近点，也可能对于某些xj在其邻域范围内不存在邻近点。

针对kantz算法存在的问题，国内学者梁勇等人提出利用可变邻域法加以改进^[1],有效减小了噪声影响。但由于在邻域上进行多点平均计算,受异常的噪声数据影响仍较大，很大程度的削弱了真实最邻近点的影响，所以在对最邻近点的逼近精度上仍有欠缺。

技术实现要素：

本发明要解决的技术问题是提供一种配电网负荷预测中的lyapunov指数计算方法。

为解决上述技术问题，本发明采用的技术方案是：

一种配电网负荷预测中的lyapunov指数计算方法，包括以下步骤：

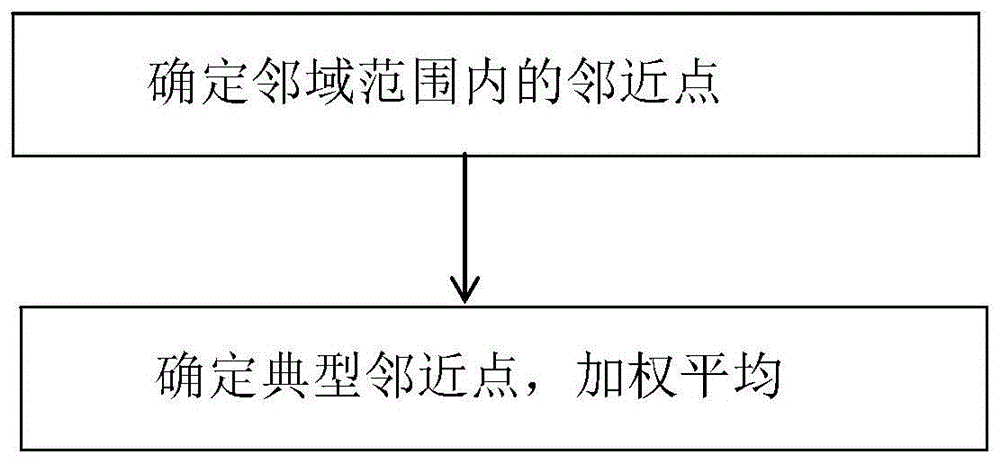
步骤1：确定邻域范围内的邻近点：确定一个相空间点xj的邻域值ε，以便在相空间点xj附近寻找其邻域ε范围内包括的所有邻近点l,l,

步骤2：确定典型邻近点，加权平均：判断ε相空间点xj的邻域ε内邻近点数目，若相空间点xj的邻域ε内仅存在1个邻近点转向步骤2-1；若相空间点xj的邻域ε内存在n(n＞1)个邻近点l,l,转向步骤2-2；否则转向步骤2-3；

步骤2-1：即为xj的典型邻近点转向步骤2-4；

步骤2-2：将以ε为半径的邻域范围以相空间点xj为球心按距离划分为n(n＞1)等份，其与球心xj的距离区间分别为：

分别统计落在每个距离区间内的邻近点数目qu(u＝1,2,l,n),在每个距离区间内选取距离球心xj最近的邻近点利用相空间重构技术，将距离球心xj最近的邻近点经过i步演化为演化模型包括局部线性预测法、局部多项式预测法等多种相空间重构预测模型；转向步骤2-4；

步骤2-3：计算相空间距离：

分布密集区域点的影响，以第u个区域内邻近点数目的平方与各区域邻近点数目平方的总和的比值作为权值；

步骤2-4：扩大邻域边缘范围至预设数值范围内；判断扩大后的邻域范围内是否存在邻近点，如果是，转向步骤2-6；否则转向步骤2-5；

步骤2-5：将搜索范围继续扩大直至将遇到的的第一个邻近点作为相空间点xj的最邻近点

步骤2-6：n(n≥1)个邻近点记作l,l,将各邻近点分别采用步骤2-2中的演化方法演化为l,l,赋以权值累加：

其中n为权值；到相空间中心点xj距离远的演化后的邻近点的权值大于到相空间中心点xj距离近的演化后的邻近点的权值。

进一步，步骤2-4中扩大邻域边缘范围1.5ε；判断邻域(ε～1.5ε)范围内是否存在邻近点。

采用上述技术方案所取得的技术效果在于：

1、本发明通过将空间相点邻域分层并赋以不同的权值，更充分地突出空间相点所在邻域内最邻近点大概率出现区间的优势，以保证对最邻近点距离估计的精确度，从而提高计算精度；

2、在寻找空间相点xj的最邻近点的步骤中能更好地排除噪声干扰，通过计算得到的最邻近点更加接近真实的最邻近点，从而提高了计算精度。

附图说明

下面结合附图和具体实施方式对本发明作进一步详细的说明。

图1是本发明的流程图。

具体实施方式

实施例1：

本发明的目的在于解决现有技术中存在的不足，针对上述现有的lyapunov指数计算方法在寻找最邻近点过程中受噪声影响严重、误差较大的问题提出一种基于改进kantz算法的lyapunov指数计算方法。本发明是在kantz算法的基础上得到启发并加以改进，又因为kantz算法是在rosenstein算法的基础上针对其步骤(ii)改进得到的，所以本算法仅针对rosenstein算法的步骤(ii)中寻找最邻近点和步骤(iii)计算演化后距离的部分加以改进：

一种配电网负荷预测中的lyapunov指数计算方法，包括以下步骤：

步骤1：确定邻域范围内的邻近点：确定一个相空间点xj的邻域值ε，以便在相空间点xj附近寻找其邻域ε范围内包括的所有邻近点l,l,

步骤2：确定典型邻近点，加权平均：判断ε相空间点xj的邻域ε内邻近点数目，若相空间点xj的邻域ε内仅存在1个邻近点转向步骤2-1；若相空间点xj的邻域ε内存在n(n＞1)个邻近点l,l,转向步骤2-2；否则转向步骤2-3；

步骤2-1：即为xj的典型邻近点转向步骤2-4；

步骤2-2：将以ε为半径的邻域范围以相空间点xj为球心按距离划分为n(n＞1)等份，其与球心xj的距离区间分别为：

分别统计落在每个距离区间内的邻近点数目qu(u＝1,2,l,n),在每个距离区间内选取距离球心xj最近的邻近点利用相空间重构技术，将距离球心xj最近的邻近点经过i步演化为演化模型包括局部线性预测法、局部多项式预测法等多种相空间重构预测模型；转向步骤2-4；

步骤2-3：计算相空间距离：

分布密集区域点的影响，以第u个区域内邻近点数目的平方与各区域邻近点数目平方的总和的比值作为权值；

步骤2-4：扩大邻域边缘范围至预设数值范围内；判断扩大后的邻域范围内是否存在邻近点，如果是，转向步骤2-6；否则转向步骤2-5；

步骤2-5：将搜索范围继续扩大直至将遇到的的第一个邻近点作为相空间点xj的最邻近点

步骤2-6：n(n≥1)个邻近点记作l,l,将各邻近点分别采用步骤2-2中的演化方法演化为l,l,赋以权值累加：

n,其中n为权值；到相空间中心点xj距离远的演化后的邻近点的权值大于到相空间中心点xj距离近的演化后的邻近点的权值。

对距离相空间中心点较近的相空间点赋予较大的权值，对距离相空间中心点较远的点赋予较远的权值。因为此时已经超出邻域范围0.5倍，必须对靠近空间相点xj的邻近点优先考虑，以防止计算结果受远距离点影响过大。

进一步，步骤2-4中扩大邻域边缘范围1.5ε；判断邻域(ε～1.5ε)范围内是否存在邻近点。