对柔性结构的实时表面形状感测的制作方法
本申请要求2018年6月22日提交的在先提交的美国临时申请no.62/688,878的优先权,通过引用将其全部内容并入本文。
本申请总体上涉及对表面形状的检测,并且更特别地涉及基于位于表面上的应变敏感传感器对表面形状的确定。
背景技术:
近年来,已经存在将柔软且可变形的结构集成到机器人系统中的趋势。目标应用包括手术[1]和康复[2],其中研究人员因为其固有的机械顺应性而利用柔软且柔性的机器人。然而,这些软机器人系统通常用来自大型跟踪系统的反馈,使用间接变量(例如纤维增强致动器中的压力)来控制,或者在开环中操作,忽略了实际机器人形状和姿势不可避免地受到环境影响的事实[3]。
结果,表面形状本身的测量已成为感兴趣的领域。一些研究利用非接触式外部设备(如立体相机和lidar)来重建3d表面[4]。运动捕获系统也被用于收集对象的局部位置信息,其中反射标记物附着在表面上[5、6]。gelsight[7]能够使用具有视觉处理技术的外部ccd相机从图像帧重建复杂表面。类似地,gelforce[8]使用ccd相机检测柔性基板中标记物的位移,以估计表面引力场。尽管来自基于相机的系统的高分辨率感测数据允许重建复杂的变形,但是这些类型的系统由于其庞大的体积和对视线的依赖性而不方便用于软机器人或独立的机器人系统。
使用设备齐全的形状传感器是另一种测量柔性3d物体的方法。可以将小尺寸的基于接触的传感器附接到物体,以确定物体表面的局部位置和取向信息。微机电系统(mems)允许集成许多小型化传感器,以提供用于全局形状重建的局部信息[9]。使用以栅格图案排列的一片不可拉伸的三轴加速度计进行了表面形状重建[10]。类似地,cheng等人[11]开发了一种人造皮肤,其由基于加速度计的刚性六边形传感器单元组成,可以提供每个传感器的相对姿态。saguin-prynski等人[12]描述了他们从取向测量进行3d曲线重建的工作,并应用多曲线进行表面重建。然而,栅格型mems传感器的限制是,由于节点之间的固定连接,它们通常具有有限的柔性和拉伸能力。由于布线,在大规模应用中使用时,它们也很复杂。
最近,例如为共晶镓铟(egain)的液体导体已被嵌入弹性体基板中,以测量完全柔软的传感器中的应变。这些传感器本质上是柔顺的,并且被设计为人造皮肤,其可以集成到完全柔软的系统中,如软机器人[13、14]。它们的基本感测原理类似于传统的应变计,需要液体金属通道任一端上的接触电极。这可以使扩展到更大或更复杂的设计成为具有挑战性的任务。
使用光纤布拉格光栅(fbg)的基于光纤的传感器是在像是土木工程[15]和航空航天工业[16]的领域具有可靠性能的传感器技术之一。fbg具有出色的抗电磁性[17],可用于恶劣环境[18],例如具有极高电磁噪声,真空压力和极低温度的环境。它们可以在单根光纤上承载高密度传感器[19],具有小形状因子和长期稳定性[20]。基于fbg传感的基于3d曲线的形状重建已越来越多地应用于连续机器人[21],例如用于活组织检查和消融的可操纵介入针[22]。然而,这些方法被指定用于管形重建,其中fbg用于监控3d曲率。为了扩展fbg在形状感测中的应用,已经提出了更多的设计。silva等人[23]设计了一种可穿戴的感测手套,用于监控手势和姿势,其中单根fbg光纤以曲线布局放在手上。在这种设计中,手套能够实时显示手部动作。然而,这是通过测量每个指关节的弯曲角度而不是从手本身的形状来实现的。这会产生对fbg准确放置的依赖性,使它们与患者的手指关节对齐。mable等人[24]在他们的3d形状传感器中实现了双层fbg网格。它需要fbg分配的精确固定,其中两个光纤层必须对齐,使得每个fbg以90°精确地彼此重叠。zhang等人[25]提供了一种用于大规模(800×800mm)板表面的表面形状重建算法,其具有正交fbg应变传感器网。传感器可以检测凸面和凹面物体表面。然而,使用相对刚性的树脂玻璃基板将变形限制为简单的形状。此外,对于采用正交光纤布局的形状传感器,整个传感器基板的拉伸能力是有限的,并且取决于强烈影响重建准确度的精确fbg定位[26]。
本发明涉及设计和制造新的柔性3d形状传感器,其可以实时重建对象的表面。
技术实现要素:
根据本发明,现有技术的问题和缺点用用于开发柔性传感器的设计框架来克服,其可以实时重建该柔性传感器3d表面形状。该传感器具有稀疏分布的下面的应变/位移感测模式或包含在柔性基板中的感测元件。在一个实施例中,单芯光纤嵌入柔性基板中。沿着光纤的长度放置了光纤布拉格光栅(fbg)形式的应变敏感的感测元件。这些fbg可以检测光纤的局部变形。通过数值分析,即有限元分析(fea)或建模,可以在制造之前为每个应用定制设计参数,例如基板厚度和感测元件的布局。fem还用于确保传感器的每个变形模式的唯一传感器元件响应(例如弯曲和扭转)。
通过使用来自fbg的稀疏传感器读数,在执行回归分析的计算机上执行的机器学习算法可用于重建传感器的整个3d表面形状。由于机器学习回归方法的可适应性本质,对于期望的应用还可以高度定制传感器的物理参数,并且不需要知道感测元件的明确布局。计算力学方法(例如fea)可用于加速机器训练或学习过程并大大提高表面形状测量的分辨率。通过首先使用模拟数据初始化训练模型,然后使用真实传感器数据进行校准,可以使用fea来减少训练。它还可以用于通过基于稀疏传感器输出数据的基于力学的插值来重建密集表面数据。
表面形状传感器的设计方法学/框架可适用于本质柔性的其他下面的应变/位移感测模态(不限于fbg),并且也可以以不同的基板类型来使用。这是由于fea模拟的灵活性和可定制性以及基于机器学习的重建方法。
可以基于应用的要求自由选择用于传感器基板的材料,要求包括机械性质,例如柔性,拉伸能力,尺寸,刚度,厚度,强度。例如,对于具有软机器人(通常由硅酮橡胶构造)的应用,平的硅酮橡胶基板促使容易集成并确保机械兼容性。类似地,对于医疗或康复用途,医用级硅酮橡胶可用作传感器基板,以允许与患者安全地长时间接触,例如,当为了触诊目的而在局部区域中测量患者的表面形状时。
在一个实施例中,将沿其长度具有许多fbg的单个光纤嵌入到平的硅酮橡胶结构中,该结构用于测量其顶表面和底表面二者上的应变。通过使用神经网络机器学习方法,基于通过光纤的光感测信号来映射由应变表示的表面位移。在该方法中,在训练的神经网络中补偿制造误差,并且降低整个制造难度。系统能够用提出的传感器进行物体形状感测。同样,它可以重建实时经受弯曲和扭转二者以及更加复杂的变形的表面。
仅使用来自fbg的稀疏传感器读数,机器学习算法可以重建传感器的整个表面形状,并且因此重建其所在的物体。由于机器学习回归方法的可适应性本质,对于期望的应用还可以高度定制传感器的物理参数。
目前,大多数表面形状传感器不能响应于平面内的负载,因为它们本质上是不可拉伸的。这使它们的感测应用限制在同样不可拉伸的表面/物体。目前的表面形状传感器系统的可定制性还受基板和感测元件的选择所限制。除此以外,对于捕获高密度数据的表面形状传感器,需要大量的单独传感器,这导致成比例大量的电连接件,这可能很大程度上阻碍易于与现有系统集成。出于相同原因,基于电极的表面形状感测装置的缩放至更大维度是不实际的。
本发明中,一个实施例采用具有光纤布拉格光栅传感器并嵌入到由硅酮弹性体制成的柔性基板中的光纤,本发明可以在不需要附加连接件的情况下容易地按比例放大,因为光纤fbg用作下面的感测元件且具有高复用性能。本发明的首要目的是为了提供可拉伸、柔性且易于扩展的表面形状感测装置的设计、制造和实施方法,该装置仅使用稀疏感测点并最少化外部连接件。
尽管本发明的一个实施例原理上依靠于传统的基于二氧化硅的光纤,但是本发明还可以扩展至各基于聚合物的光纤,其可以提供增强的柔性和伸长率,同时保持相似的光学性能。在基于聚合物的光纤的情况下,表面形状传感器的柔性和变形度被改进,以允许测量更加复杂的表面形态。
总之,本发明的表面形状传感器可以具有其基于稀疏的感测元件数据来密集地重建的表面形态(以及因此其附接于的物体的表面)。传感器体/基板由柔性材料制成且嵌入柔性应变感测元件。传感器的功能可以通过以下来实现:
1.在制造之前引导传感器的计算力学建模(例如,fem/fea),以定制传感器的参数,例如,传感器尺寸和传感元件的放置,以及
2.使用ai(例如神经网络的非线性回归方法)和计算力学建模,以校准传感器和重建传感器的形态。
附图说明
本专利或申请文件包含至少一个彩色图。具有一个或多个彩色附图的本专利或专利申请出版物的副本将基于请求和支付必要费用由主管局提供。
基于参考以下的详细描述和附加的附图,本发明的前述和其他目的和优点将变得更加显而易见,其中在各种视图中相同的标记表示相同的元件,并且附图中:
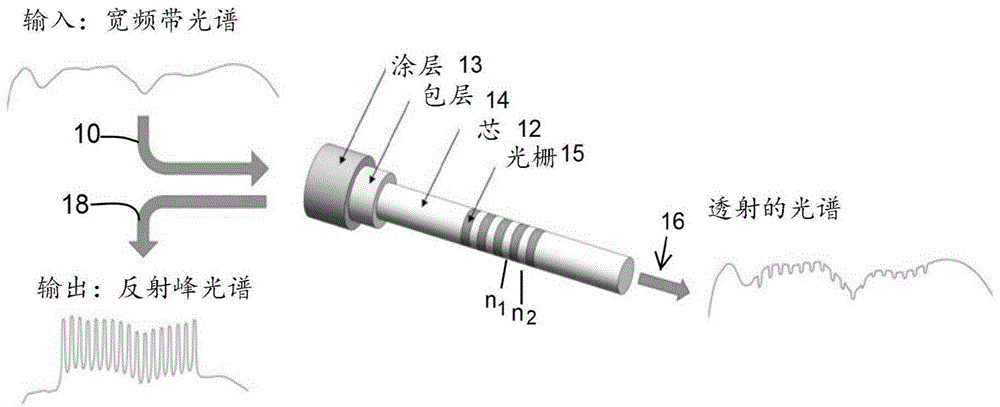
图1示出了fbg的操作原理;
图2图示了根据本发明的示例性实施例的整个传感器结构;
图3a-3d图示了传感器的有限元建模;
图4示出了在三点弯曲下的五个偏移距离处本发明的传感器的模拟的fea应变响应;
图5a-5c示出了在三点弯曲下的本发明的传感器的模拟的fea应变响应,其中传感器的厚度分别为2.5mm、5.0mm和7.5mm;
图6a-6d示出了制造根据本发明的传感器的步骤;
图7图示了在本发明的光纤中fbg的配置;
图8是由均方差方法评估的神经网络训练性能的曲线图;
图9是根据本发明的训练数据收集的运动捕获设置的照片;
图10示出了在不同变形下各种模拟的fea光纤应变;
图11是本发明的整个感测系统的示意图;
图12是训练的神经网络的误差直方图;
图13a是传感器表面的变形的3d示例,图13b是对图13a的表面形状重建的分析的位移误差直方图,以及图13c是其重建误差直方图;
图14a-14e是示出了具有周期性负载的传感器中的每个fbg的波长移位的重复性的图,其中图14a示出了分别在无偏转、向上偏转、向下偏转的条件下的传感器,图14b示出了8个fbg的波长移位波动,图14c示出了在峰值弯曲处的8个fbg的波长移位,图14d为图14b中的一个fbg的波长移位波动的一部分的放大图,图14e是比较图13a中的远端节点c2的垂直位置和具有最大移位的fbg的波长移位的滞后图;
图15a和15b示出了在表面形状的照片及其重建之间的比较;
图16a是软刺鳐模型的侧翼的表面形状感测的示例,以及图16b是该模型的照片;
图17是振动感测布置的曲线图;以及
图18示出了根据本发明的另一实施例的传感器的布局。
具体实施方式
本发明采用具有在硅酮橡胶片中嵌入的稀疏分布的光纤布拉格光栅(fbg)的单个光纤。fbg可以捕获传感器的顶表面和底表面中的机械应变,并且应变数据用于重建整个传感器表面形态。因为传感器可以布置在物体的表面上,所以它还可以重建物体的表面形态。根据本发明,将一个单芯光纤盘绕在硅酮基板内,使得它形成两个层。这确保了唯一的光信号与特定传感器弯曲配置相关联。
在本发明的系统中fgb被选择为感测元件,因为它们易于制造和组装。此外,fbg具有极好的抗电磁性和耐腐蚀性,并且可以在单个光纤上提供高密度的传感器。
fbg具有高复用性能,所以它们完美地使用于不同规模的应用的感测网络。为了使得本发明的表面形状传感器为柔性的并且是可适用的,必须考虑以下的三个主要的设计因素:
柔性
软机器人通常与它们的工作环境高度兼容。与软且可变形的机器人集成的传感器必须足够柔性地与机器人本体和围绕物兼容。因此,硅酮橡胶被选择作为基板层,用于与用硅酮制造的普通软机器人高度兼容并固定结合。
拉伸能力
表面形状传感器通常设计为格栅形式的感测网络。然而,这个配置特别是在平面内负载存在时,可能严重限制柔性和拉伸能力的程度。由于拉伸,平面内负载通常被发现在软机器人应用中。本发明的传感器中的光纤布局允许在不同方向上的拉伸能力。因为需要随应用改变拉伸能力,可能需要考虑传感器放置。
可靠性
与刚性机器人相比,期望软机器人适当地响应于与未知环境的接触。fbg对包含剧烈的温度变化和化学腐蚀的恶劣环境提供极好的耐受性[27]。这确保了传感器的长期稳定性和可靠性。在本发明的情况下,选择拉丝塔光栅(dtg)来代替常规fbg。dtg由拉丝塔工艺制造且提供了超过传统的fbg的机械强度四倍的机械强度。
本柔性形状传感器的感测原理基于全局和局部应变感测。当由弯曲负载、扭转负载或其他变形使传感器变形时,在从位移/变形生成的应变场的情况下,硅酮橡胶中嵌入的fbg传感器经历唯一的位移。以特定转移率将应变转移到fbg传感器上,这取决于制造和结合质量。沿光纤分解的轴向应变然后被转换为光信号,其中不同应变将导致由fbg积分器测量的不同波长分量。通过映射应变-位移,确定形状重建。在3d弹性中,应变ε和位移u之间的关系限定为:
其中k总和超过1、2和3,
fbg是一种本征光学传感器,其响应于环境参数。在每个光栅中,通过将光纤横向暴露于具有周期性图案的强紫外(uv)光束来永久增加纤芯的折射率。通过uv曝光的图案来固定和确定折射调制率。
少量的光(典型地大约10%)在每个光栅处被反射。当入射光近似于光栅周期的两倍时,由于fbg的复用性质,反射光信号以反射光谱的形式被传输回来。发生该反射的波长称为布拉格波长,并且该条件已知为布拉格条件:
λb=2neλ(2)
其中λb是反射的波长或布拉格波长,ne是有效折射率,并且λ是光栅周期。相位失配的波长将不被反射,因此传输到如图1所示的光纤端部。因为波长仅在满足布拉格条件时才反射回来,衰减和信号变化通常可以被忽略。这展示了光纤布拉格光栅确保光栅波长测量的高准确度的基本优点。
如图1所示,每个fbg15具有将光的特定波长反射的固定的折射率调制n1、n2等。光谱10被引入到光纤中,该光纤由轴芯12和覆盖有涂层13的包层14构成。具有不满足布拉格条件的波长的光将简单地穿过光纤传输并且将在光纤的端部出射作为光16,即透射的光谱。满足布拉格条件的光将反射回来作为光18,即反射的光谱。由于光栅参数的温度和应变的依赖性,反射的波长还将改变,因此使得感测应变/温度成为可能。
等式(2)示出了反射的光谱的中心波长或布拉格波长的移位,取决于有效折射率和光栅周期,它们是温度和应变二者的函数。因此,当传感器经历温度变化或外力时,感测响应变化。当外力被施加到传感器时,沿着整个光纤将诱导压缩或拉伸应力。传感器变形将转移为一系列光纤应变,其与应变转移率和结合质量相关。所生成的改变光栅周期和有效折射率的机械应变导致了布拉格波长的移位[28]。在包含温度影响的情况下,这允许应变和温度测量实时地反映在fbg光谱中。该依赖性描述如下:
其中δλ是波长移位,λ0是制造时的基础波长,k是应变因子,并且δt是单位为k的温度改变。αδ是折射率的改变:
其中n是光纤的折射率。对于应变ε,存在:
ε=εm+εt(5)
其中εm机械诱导的应变分量,并且εt是温度引起的应变。
εt=αspδt(6)
其中αsp是样品的每k的膨胀系数。
将等式(5)和等式(6)代入到等式(3)中,我们得到
因为光纤具有高纵横比的圆柱形几何形状,与横向应变或平面外应变相比较,fbg对纵向方向上的应变是高灵敏的。等式(7)中第一个表达式描述了机械应变的影响,并且第二个表达式是指玻璃折射率n的改变和温度应变,这仅取决于温度。从样品应变诱导出温度应变。因此,样品热膨胀系数被认为代替了玻璃的热膨胀系数。
因为温度对感测信号具有影响,所以不得不进行温度补偿以便于得到精确应变测量。常规地,附加的温度光栅被施加以校正其他应变测量光栅。最简单的方式是仅使用位于零机械应变位置处的fbg传感器来测量温度。将εm=0替换到等式(7)中,由此补偿fbg的波长移位δλc和主动机械应变测量fbg的得到的位移移位δλm由以下给定:
对于用于应变感测的fbg,等式(6)可重写为:
然后,如果我们将等式(8)代入到等式(9)中,则我们得到
其中λ0c是补偿fbg的中心波长,并且λ0m是机械应变测量fbg的中心波长。
对于初始简化的示例性实施例,为了便于制造,对于传感器基底选择矩形几何形状。特别地,传感器基底由硅酮橡胶正方形(45mm×45mm)模制,以及在传感器的顶部和底部上以35mm的直径圆形地包裹fbg传感器。fbg传感器以偏离中间平面的距离放置以避免从不同变形模式形状中得到相同传感器响应,例如从具有同样大小的弯曲矩的正向或负向弯曲可能得到相同弯曲应变。
整个设计包含五层,即中间传感器基底基板层,两个fbg传感器层和两个硅酮保护层,如图2所示。除了光纤传感器层外的所有层由硅酮橡胶(smooth-onecoflex-0030)制成。保护层是在fbg层上方的薄涂层并且对传感器刚性和柔性具有可以忽略的影响。
因此,整个传感器结构如下:i)顶部薄硅酮保护层、ii)第一fbg层、iii)硅酮板、iv)第二fbg层和v)底部薄硅酮保护层。从中间平面到光纤的距离限定为h,并且传感器厚度限定为t。在操作期间,将光纤的一个端部连接到从嵌入式fbg撷取信号信息的光询问器(interrogator)。然后在使用神经网络进行非线性回归的程序中处理该信息,以实时重建3d表面形态。
fbg传感器或光栅被写入定制的低弯曲损耗光纤(fbgslbl-1550-125,
为了为传感器厚度t和光纤偏移h选择适当设计参数,引导参数研究以评估具有不同传感器设计的传感器性能。设计的形状传感器的评估和预测的传感器响应从商用有限元分析软件abaqus6.14计算出。采用有限元分析,是由于它在计算具有各种传感器几何形状的传感器响应中具有高适应性。在该研究中,研究两个选择的参数。
图3示出了分析传感器参数的流程图。部分模型首先用设计的尺寸来构建。硅酮传感器基底和传感器光纤被建模为3d可变形模型。在简化的模型中不包含保护层,因为它们对总传感器刚性具有可以忽略的影响。然后将材料分配到模型。对于硅酮橡胶,它被建模为使用ogden应变比能的超弹性材料。3项ogden模型的参数选自文献[29]:μ1=0.024361,μ2=6.6703×10-5,μ3=0.45381×10-3,α1=1.7138,α2=7.0679,α3=-3.3659,d1=3.2587,d2=d3=0。μ和d的单位分别是mpa和(mpa)-1,而α的单位是无量纲的。
为了建模光纤材料的机械行为,使用图3c的线性弹性模型,其中杨氏模量为70gpa,并且泊松比为0.16。图3d显示的最终传感器基底被网格化为648个c3d8rh砖块元件(18×18×2),并且传感器光纤被网格化为44个t3d2h桁架元件,其是仅转移轴向应变的2节点线性3d桁架单元(trusselement)。光纤部件以节点区域到表面的约束被束缚到期望的传感器基底表面。为了在不同负载条件下模拟传感器响应,传感器的一侧设定为夹紧的条件(图3d的左侧的红色点),而其他作为自由端是无界限的。在静态负载步骤下完成所有模拟。为了生成诸如弯曲和扭转图案的变形,图3b中表面负载被施加在标记为红色方形的12个表面上。
因此,有限元模型流程图如下:
(a)部件模型和组装件:硅酮板和光纤用期望的尺寸来构建。硅酮保护层由于低厚度是可忽略的。光纤模型以表面到节点区域的约束被束缚在硅酮板模型的表面上。
(b)网格化:硅酮板模型(45mmx45mmx5mm)被网格化为5184个c3d8rh元件(36×36×4),并且传感器光纤被网格化为44个t3d2h元件,其是仅允许轴向应变的2节点线性3d桁架。
(c)负载和表面集定义:将12个表面集预先定义为施加随机压力负载,以模拟在节点旋转之后在传感器表面上作用的外力。
(d)边界条件:传感器的一侧以夹紧的条件为界限,而其他作为自由端是无界限的。
在图3中,从模拟输出获得传感器的顶表面上x、y和z位移场以及轴向光纤应变。在这些模拟中没有考虑温度影响和预先应变。从等式(10),波长移位和机械应变之间的关系可以描述为δλ~εm。这指示了模拟的传感器应变响应和波长是相关的,其可以用于预测实际传感器响应。
考虑在厚度t任意地设定为5mm时光纤偏移距离h的效应。根据弯曲理论,当传感器经受正向和负向弯曲矩时,沿着中性平面的应变是相同。这指示了fbg必须从中性平面偏移,以标识弯曲的方向。在图4中,当传感器放置在两个支撑销上并通过位移具有20mm的半径的圆柱来经受负载f时,获得每个传感器响应。这模拟了典型的变形图案,其中通过按压创造弯曲。当光纤从中间平面h=0mm偏移时,模拟的应变由于通过按压诱导的平面内应力而略微为正。对于纯弯曲,当不考虑预应变时,传感器将具有近似零的应变读数。当h=+0.25t=+1.25mm时,观察到应变幅度的显著升高。当h=-0.25t=-1.25mm时,由于压缩负载,模拟的应变移位到负的区域。当h=±0.5t=±2.5mm时,观察到应变的进一步增加。然而,在压缩应变灵敏度中的增益更低。注意到当光纤在压缩时,它可以在有利的方向上弯曲。因此,与拉伸负载相比较,变形的光纤将经历幅度较低应力。为了最大化应变幅度以更好区分应变图案,选择最高偏移值,即h=±0.5t=±2.5mm。
图4示出了在三点弯曲下五个偏移距离h处的传感器的模拟的应变响应。每个简化的光纤环模型在例如h=0处的对应的平面中测量应变,光纤嵌入在中间平面。来自压缩应力的负应变的幅度在与来自拉伸负载的正应变相比较时是小的,因此小h处的感测应变是不太有利的。注意到中性平面不必与中间平面相同,并且取决于平面内和平面外的负载。
引导第二分析,以研究传感器基底的厚度t。对于软且柔性的传感器,当将传感器集成在例如致动器及其他组件的物体上时,低厚度是有利于柔性。然而,因为使用单芯光纤,光纤需要从中间平面偏移并必须具有适当的厚度以便于辨别变形图案。通过考虑具有变化厚度(2.5-7.5mm)的应变图案来确定厚度t。参见图5。范围通过考虑足够高的整个传感器厚度来选择并将不禁止柔性的运动。在第一分析中,推断出传感器光纤应该附接到传感器的表面,以获取最大应变响应。在图5中,在如图4的相同弯曲下,仿真传感器结构的应变响应。当传感器基底厚度t接近于传感器光纤直径的十倍,即t=2.5mm时,压缩应变响应由于重叠而不足以标识形状图案,并且可能由传感器噪声来更改。通过增加传感器厚度,输出响应还增加并变得显著。在t=7.5mm处,传感器响应最大化。然而,有些压缩应变开始饱和。其他变形可能诱导不利的压缩应力并导致不稳定性,光纤的弯曲和硅酮板内的光纤的最终断裂。在将传感器响应与更多变形模式进行比较后,对于主要形状选择5mm作为最佳传感器厚度,以便于产生区别的应变图案同时提供高柔性。取决于机器人设计和感测需求,对于最佳性能可以调整传感器厚度。
图5示出了在三点弯曲下不同厚度处的传感器的模拟的应变响应,其中偏移h=±0.5t。应变的幅度与传感器厚度成比例地改变。在厚度t=2.5mm处,应变由于压缩负载而重叠。在厚度t=5mm处,负应变可以被清楚地识别并用于辨别变形。在厚度t=7.5mm处,灵敏度与若干尖锐点一起进一步增加,然而,这还导致不稳定的较高可能性、光纤弯曲和较低柔性。
通过铸造铂催化的硅酮(即ecoflex00-30)来制造表面形状传感器。ecoflex硅酮由于它们的低粘度而被选择,其促成在制造中混合和排气,以及与共同使用相似硅酮的当前软机器人的高结合强度。对于不同光纤配置设计了具有特殊图案的模型。因为这个设计聚焦在一般表面感测和结构简化,所以使用圆形光纤配置。
如图6a所示,硅酮的混合部分被排气并注入到已经用释放剂涂覆的3d印刷的模型中。然后它在烤箱中以55℃保持60分钟。之后发生脱模,其中将具有设计的通道的固化的硅酮从模型中移除(图6b)。在脱模图案化的硅酮板后,用针穿透板的顶表面和底表面,以放置光纤(图6c)。因为通过将光纤成形到目标配置来诱导应变,小的销用于将光纤形状临时地固定在硅酮板上,因此避免使光纤回到中性位置。
在图7的示例性实施例中,在硅酮板中嵌入的光纤布拉格光栅由强紫外光在光纤芯上曝光来制成。固定折射率调制(即光栅)被创造并且增加,以永久设定芯折射率。光纤具有125μm的包层直径,并涂覆有ormocer(创造195μm的直径)。每个光栅具有5mm的长度,实际上较小的长度也是可用的。针对前面的16个fbg,每个光栅以10mm间隙分离,并且在第16个和第17个fbg之间的距离fbg是450mm。这16个fbg覆盖硅酮板的两个表面以捕获应变信息,并且剩余的第17个fbg用作温度补偿传感器。为了易于组装,远离第16个fbg来定位第17个fbg。第一光栅开始于1588nm处,最后一个光栅结束于1540nm处。每个fbg反射峰的中心波长具有与其近邻3nm的波长分离,以防止反射峰的重叠并确保清楚的峰标识。取决于应用,可以对于较多/较少的fbg调谐分离。具有较短波长(例如,1540和1543nm)的光栅靠近地位于光纤引入端,而具有较长波长的光栅接近地放置在引出端。在光纤中传播的大部分光能被限制在芯中,而剩余的光能在包层中行进。因为反射的布拉格波长越短则光损耗越大,所以具有较短波长的fbg接近地放置于引入端。光纤的反射率大于10%,并且半高宽(fwhm)是0.15nm。光纤是对弯曲不灵敏的并且具有多达6mm的弯曲半径。反射的光谱由用作询问器的光谱分析器(anritsums970a)来捕获。
任何局部变形发生在传感器的一侧,应变将根据变形位置来生成并导致单独的光栅响应。对于在传感器的中心的变形,期望的是,生成全局光栅响应但是具有较低幅度,因为光栅围绕中心但是不与合成应变对准。使用这些光栅响应的组合,传感器重建并辨别不同变形模式形状,其包含在软机器人中通常看见的弯曲和扭转姿势。
人工神经网络由改变它们内部激活状态并在接收输入时生成输出的神经元的网络构成。指定的神经元的输出和输入彼此连接并形成直接且加权的图。用期望的学习函数在选择的训练过程期间计算权重。可以通过变化管理学习规则来调整网络的性能,并因此对神经元和激活加权。这个数据驱动的方法通常需要模型训练的大量样本,其将输入变量映射到目标输出。典型的神经元传递函数如下:
o=f(∑wiii)+b(11)
其中o是标量输出,f是s型(sigmoid)函数,wi是第i个权重,ii是第i个输入,以及b是偏置。
为了证实映射的唯一性和预测传感器准确度,从用于训练的有限元分析(fea)数据中提取表面信息(即位移数据)和模拟的应变响应。使用如上限定的有限元模型,压力负载随机生成在如图3d所示的高亮的表面(如右侧的红色箭头)上。压力负载的使用创造了平滑变形表面,而不是将集中力施加到特定元件或节点上,这可能易于使元件失真。在限定的压力范围下,完成729次模拟,其中每一个包含10个步骤。因此,生成7290个数据集。如图10中示出一些模拟的响应。将节点的x、y和z位移提取作为目标输出,而光纤应变(应变图案)被限定为网络输入。
具有两层的典型的多层前馈网络用于训练。第一隐藏层包含连接到输入的10个神经元,并且第二层产生网络输出。隐藏层的传递函数是双曲正切s型函数,并且输出层的函数是线性传递函数。神经网络的输入是光纤桁架元件中的44个稀疏的轴向应变,并且输出节点来自于1083个位移数据。因为网络大并对于计算需要较少内存,使用量化共轭梯度反向传播。当在实际传感器原型中缩减网络尺寸时,替代地可以使用levenberg-marquardt反向传播方案。它使用以下规则更新网络:
wk+1=wk+δwk(13)
其中wk、wk+1是在步骤k和k+1处更新的网络。
其中ti是来自训练的网络的输出位移,oi是实验中的实际位移。
其中j是每个误差相对于每个权重的的导数的雅可比(jacobian)矩阵。
根据牛顿方法,
然后将等式(17)和等式(18)代入到其中,则我们得到
δw=-[jr(w)j(w)+μi]-1jt(w)e(w)(19)
i是单位矩阵,μ是在迭代期间适应性改变的标量,以及e是误差矢量。
神经网络性能通过均方差(mse)来评估:
其中ui(actual)是实验中第i个实际位移,并且ui(nn)是来自训练的网络的第i个输出位移。当性能梯度的幅度小于le-6或验证性能停止递减时,训练停止。大约70%的数据用于网络训练,15%用于验证以及最后15%用于测试。神经网络训练结果示出了具有r平方值为0.989(即整体上误差小)的良好拟合。光纤元件的轴向应变被设定为神经网络输入,并且顶表面节点位移设定为神经网络输出。在5855次时,最佳验证性能为0.055439mm。高回归系数隐含表面位移和fbg应变的唯一映射。这还指示,建议的光纤配置被良好定位并且能够准确地表示并重建传感器表面。均方根差为0.2354mm并且最大误差为5.3485mm。
如图9所示出,为了在变形的表面上捕获数据,传感器被夹紧至仅在一侧限制位移的刚性固定器。optitrack运动捕获和跟踪系统使用两个flex3相机以撷取表面位移信息,其将基础事实数据提供给神经网络训练。术语“基础事实”是指用于监督机器学习技术的训练集分类的准确性。在该实施例中,运动捕获是收集该神经网络的适当目标(可证实)数据或基础事实的过程。被动标记物放置在传感器表面,以反射用于跟踪的ir光。因为硅酮表面具有低表面能量并难以牢固地附接标记物至表面,首先将loctite495粘合剂施加到表面以及使小纸带与传感器结合,以允许感测标记物的位置。在捕获数据之后可以容易地移除纸带。流速率是每秒100帧,并且标记物的总数因为跟踪系统的限制而是9个。在校准之后,平均定位误差是0.015mm。
在训练阶段,用于获得传感器的表面形状基础事实的方法不限于使用运动捕获系统。任何可以获得关于传感器的3d表面形状的信息的设备都适用于该传感器设计框架。示例包括:基于电磁的跟踪系统,单目/立体相机系统,激光扫描系统。
图10示出了在不同变形下各种模拟的光纤应变。第一列示出了在不同负载组合下的变形的传感器形状。第二列是变形的光纤在e11方向上的弹性应变分量的色彩图。较暖的颜色指示了光纤上诱导的较高的应变。第三列示出了模拟的光纤应变图案,其是标识和辨别不同变形模式的基础。应变响应被设定为神经网络输入,并且节点位移被设定为目标的神经网络输出。
图11是本发明的整个感测系统的示意图。它包含光源30、fbg形状传感器36和fbg询问器34,它们由三端口的光环形器32来连接。在大多数入射光谱10传输到传感器36的光纤的端部42的情况下,反射的光谱18进入fbg询问器34并由fbg询问器34捕获。然后将光信号发送到处理器或个人计算机(pc)38以计算反射的波长。
在示例性实施例中,光源可以是amonics的ls-cl-gff-18-b-fa,其将从1500至1595nm的宽频带可见光经由光环形器(其可以是pioc-3-cl-p-90-10-fa)传输到光纤36。由于芯折射率的依赖于应变的改变,光从光纤36反射。从光环形器的输出端口将反射的光谱发送到fbg询问监控器34(i-mon512usb)。因为光是可复用的,在光纤上每个光栅处反射的光总计为反射的光谱。这个询问系统可以用小于0.5pm的波长分辨率和3000hz的最大测量频率来感测和标识超过70个fbg。布拉格波长通过峰值搜索算法来识别并被发送到处理器,用于分析和表面重建。
为了生成不同的且复杂的变形图案,传感器被手动弯曲而不阻挡用于感测的跟踪标记物。线性致动器阵列由于尺寸限制和在控制传感器自由度中的低柔性而不用于生成负载图案。这可能在致动器端部没有固定到传感器时容易阻挡标记物,或者可能在牢固固定时引起传感器的损坏。因为系统以高采样率使用光询问系统和运动跟踪系统,手动地变形传感器允许了复杂图案变形具有短采样时间。大约具有对应的布拉格光谱的1000个姿势被捕获并用相同神经网设定来训练。尽管可能存在制造缺陷和光纤位错,但是在训练神经网络时自动包含这些误差,因而不需要校准。
在本发明的测试中,观察到相似的布拉格波长图案并且它们符合模拟结果。在该文本中,16个具有温度补偿的布拉格波长被设定为输入,并且27个位移被限定为输出,以便于建模波长和位移的关系。所有重建的位移节点的均方根(rms)误差为0.9234mm并且最大误差为4.81mm。参见图8。与fe模拟结果相比较的rms误差的升高可能来自测量噪声、校准误差和简化的fe模型的使用。然而,感测准确度仍然超过现有的形状感测装置的准确度。
常见变形模式形状(例如弯曲和扭转)还可以由训练的网络来重建。参见图10。可测量的弯曲曲率为从0至0.04mm-1。使用matlab表面绘制功能,表面感测循环的刷新率超过10hz。更高的刷新率通过使用具有更好的图形能力的其他程序来实现。
图12是训练的神经网络的误差直方图。实际位移(即图9所示出的跟踪标记物位置)被设定为目标输出。大约70%的数据用于网络训练,15%用于验证以及最后15%用于测试。均方根误差为0.9234mm并且最大误差为4.81mm。
图13的各种图表示表面形状重建的准确度分析。在该分析中,可以通过将ann估计的输出坐标与ir跟踪基础事实进行比较来获得感测误差。在图13a中示出了样品变形情况,其中传感器固定在一个端部处并且另一端部从中性位置向上弯曲。在表面重建样品中,示出并记录九个标记物[a1、a2、a3、b1、b2、b3、cl、c2、c3]的彩色轨迹。颜色越暖(朝向红色),相对于基础事实的位移误差越大。图13b示出了1350个样本中所有节点的位移误差分布的直方图。大多数节点位移误差大多低于2mm。在距离夹紧侧(固定端部)更远的节点中看到更大的误差,即图13a中的c1~c3。对于节点c1~c3,均方根误差(rmse)约为1.8mm。相反,节点a1~a3和b1~b3的误差较小,所有节点的rmse均为1.17mm。所有节点位移的rmse如图13c所示。通常,节点位移误差随着距固定端部的距离而增加。这可归因于ann训练数据中节点位置的分布。每个节点具有相同的总样本,但是与节点a1~a3和b1~b3相比,自由端部处的节点c1~c3具有更大的位移范围。这导致较少空间密集的样本点,因此远端节点的训练性能较差。这可能是节点c1~c3处增加的重建误差的主要原因,如图13c所示。
进行可靠性测试以确保在长操作期间的一致响应。通过推动/拉动节点c1~c3的3个线性致动器产生许多重复的传感器运动周期,这导致传感器的周期性加载。如图14a所示,传感器被夹紧到固定器上,自由端部向上,向下弯曲,最后在2秒内回到中性位置。在50分钟内进行总共1000次弯曲循环,在向上运动的峰值处记录布拉格波长响应。图14b示出了一层上八个fbg的反射波长移位。在图14d中提供了一个图的一部分的放大或放大视图。可以观察到波长移位值在恒定值附近略微波动。箱线图(图14c)显示了八个波长移位的分布。对于所有fbg,波长波动保持在0.01nm以下,对应于0.3mm位移。这表明传感器可以在全部1000个变形周期内保持稳定和可靠的响应。图14e是比较远端节点c2的垂直位置(图13a)和具有最大移位的fbg的波长移位的滞后图。传感器向上弯曲并返回平坦位置3个循环。
图15b示出了表面形状重建的示例。力被施加到传感器并在传感器表面引起变形(图15a)。传感器表面通过训练的神经网络来重建(图15b)。色彩图指示表面的深度。
图16a示出了软刺鳐的侧翼的表面形状感测模型的示例。图16b中示出了模型的照片,其中传感器被修改并嵌入到模型中。将模型放置在具有振荡流的水槽中,并且如与水流流动相对的翼形状一样来实时地重建翼形态。在这种情况下,软且柔性的机器人的形态和游泳移动可以直接使用表面信息反馈来学习。
其他示例用于在柔性装置上估计自激发的振动或外部激发的振动。代替表面重建,连续地捕获位移数据以构造振动波形并计算振动周期。因为在整个传感器之上局部地捕获布拉格波长响应,在各种位置处的动作捕获和补偿在来自传感器的反馈的情况下是可能的。图17示出了传感器的示例性响应,其中脉冲负载被施加在传感器的自由端(即与夹紧边缘相对的一侧)上。脉冲在传感器中生成振动。因为高采样率可用于传感器,所以在波长历史中捕获动态响应。这使对软机器人的振动测量和控制成为可能。观察到具有小相位差的相似的波形,该相位差指示了振动频率和波传播。这可以施加到游泳步态感测和反馈控制。
尽管本发明具有合理的柔性和拉伸能力,但完全平面内负载引起的可允许应变仍然很小。它受到限制变形的刚性光纤的限制。结合传感器的小尺寸,无法测量更复杂的变形而没有损坏光纤的风险。通过改变光纤布局可以进一步提高传感器的柔性,但这需要考虑其他因素,如光纤长度,fbg数量以及与整体传感器灵敏度的权衡。本发明的传感器的另一个限制是压力灵敏度。向传感器施加压力可以在fbg中引起应变而不会引起表面本身的大的变形。这可能导致使用当前方法的不正确的形状重建。可以实现能够将局部压力刺激与一般形状重建区分开的技术。这将能够同时测量形状和力,这对于触觉应用尤其重要,并且压力差异最终可以减少重建误差。此外,根据本发明,可以补偿传感器附近的环境温度变化。然而,在每个fbg处补偿局部温度变化仍然存在一些困难,这是使用一个单芯光纤的固有缺点。
诸如光功率测量和超声群集束注入(scbi)[30]的其他技术可以用于提供信息,以区分不同刺激。
本发明涉及高准确度表面形状传感器。使用光纤,表面信息通过光谱来测量并通过机器学习算法来映射。进行有限元模拟,以研究、分析传感器参数并预测感测响应和准确度。软且柔性的表面实时地提供在软机器人和其他潜在应用中有用的表面形态信息。本发明的主要特征为:
1.仅利用单芯光纤实时检测表面形状的变化。许多现有技术研究通过使用多芯光纤或捆绑多个单芯光纤来重建光纤本身的形状。在这些示例中,仅重建实际的光纤形状,而不是如本发明那样的表面形状。另外,由于制造成本和对多通道光学询问器的要求,使用多芯或多个光纤会增加传感器的总成本。
2.下面的光纤传感器不限于传统的基于二氧化硅的光纤,并且可以扩展到使用基于聚合物的光纤,其可以提供增强的柔性和伸长率,同时保持与常规二氧化硅光纤类似的光学性能。使用基于聚合物的光纤,改善了表面形状传感器的柔性和可变形性。
3.当缩放到更大的尺寸时,由于其光学性质,所提出的传感器的物理输入/输出的数量保持不变。基于电极的传感器(例如使用加速计的传感器)需要额外的接入电极,因为传感器中的感测元件的数量增加,使得它们对于缩放到更大尺寸或更高密度感测而言是不实际的。
4.详细的fea建模用于确定设计参数并验证传感器的唯一性。通过fea实施计算机辅助分析,可以预先确定传感器参数,以优化下面的传感器布局并根据每种应用进行定制。基础传感器形状不限于矩形片,并且可以基于期望的应用自由地改变。
5.机器学习的应用提供了3d表面形状重建,其对于传感器制造期间不可避免的不准确性更加鲁棒。
6.在训练阶段,通过使用模拟数据样本初始化训练模型,fea可用于加速机器学习过程。完全基于该fea初始化的形状重建将不是完全准确的,因此可以使用少量实际数据来执行校准。通过这种方式,可以在数字环境中快速且自动地执行大部分训练过程,从而减少对耗时且昂贵的实际数据收集的依赖。
7.在形状重建阶段,fea可用于通过在基于机器学习的重建模型输出的稀疏位置节点之间精确插值来增加感测分辨率。例如,如果在训练机器学习算法时使用使用稀疏分布的反射节点(将每个节点的3d位置作为传感器基础事实)的运动捕获系统用作输出,则可以通过使用基于fea的模拟模型进行插值来改善形状重建的空间分辨率。
8.在本发明的实时形状重建期间,不需要诸如相机的外部视线传感器。
9.表面形状传感器的设计方法学/框架可适用于本质柔性的其他下面的应变/位移感测模式(不限于fbg),并且也可以以不同的基板类型来使用。这是由于fea模拟的灵活性和可定制性以及我们基于机器学习的重建方法。
10.在所提出的实施例中,使用运动捕获系统获得传感器的训练数据,该运动捕获系统收集附着到传感器表面的红外标记物的3d位置。获得这种“基础事实”的其他方法可以代替用于本发明的设计方法学,例如,电磁(em)传感器系统,用于3d重建的立体相机,基于激光的3d传感器,单目相机等,即可以提供传感器表面的基础事实测量的任何传感设备。
在本发明的另一个实施例中,它利用基于fbg的传感器的相同设计和重建方法学,然而,下面的感测元件已经变为共晶镓铟(egain,液态金属)应变传感器。感测元件的结构类似于传统的应变计,并测量两个终端之间的电阻变化以测量应变。然而,代替嵌入硬塑料中的刚性金属线迹线,egain传感器使用嵌入柔性基板(如硅酮树脂)中的液态金属通道。当感测元件被拉伸时,通道收缩并伸长,导致电阻增加。感测元件通常设计成基于导线迹线布局在其纵向方向上更敏感。
在该实施例中,这些应变感测元件中的多个嵌入柔性弹性体基板中以获得用于形状重建的局部应变数据。在该实施例中,可以以相同的方式应用fea和机器学习。请注意,在这种情况下,感测元件是独立连接的,与沿单个光纤的fbg不同。如图18所示,传感器以栅格状布局,但它们可以任意放置(或根据fea制定的设计决策)。注意,在该实施例中每个应变测量需要两个(2)连接电极。这只是可以使用的感测元件的另一个示例。其他的可能不一定需要这么多的连接电极。
在又一个实施例中,下面的感测元件可以是具有高复用性能的任何感测元件。
在一个实施例中,柔性基板可以是编织织物。在其他实施例中,柔性基底可以是薄且柔性的塑料或金属片。在又一个实施例中,柔性基板可以是传感器能够固定到其上的任何柔性材料。
参考文献:
下方列出的参考文献被引用在整个说明书中并且由在方括号[]中放置的对应编号来标识。以下参考文献中的每一个通过引用全部并入本文中。
[1]k.-h.leeetal.,″nonparametriconlinelearningcontrolforsoftcontinuumrobot:anenablingtechniqueforeffectiveendoscopicnavigation,″softrobotics,vol.4,no.4,pp.324-337,2017.
[2]ppolygerinos,z.wang,k.c.galloway,r.j.wood,andc.j.walsh,″softroboticgloveforcombinedassistanceandat-homerehabilitation,″roboticsandautonomoussystems,vol.73,pp.135-143,2015.
[3]c.laschi,b.mazzolai,andm.cianchetti,″softrobotics:technologiesandsystemspushingtheboundariesofrobotabilities,″sci.robot.,vol.1,no.1,p.eaah3690,2016.
[4]g.sansoni,m.trebeschietal.,″state-of-the-artandapplicationsof3dimagingsensorsinindustry,culturalheritage,medicine,andcriminalinvestigation,″sensors,vol.9,no.1,pp.568-601,2009.
[5]f.saunders,e.golden,r.d.white,andj.rife,″experimentalverificationofsoft-robotgaitsevolvedusingalumpeddynamicmodel,″robotica,vol.29,no.6,pp.823-830,2011.
[6]m.k.dobrzynski,r.pericet-camaraetal.,″contactlessdeflectionsensorforsoftrobots,″inintelligentrobotsandsystems(iros),2011ieee/rsjintemationalconferenceon,2011,pp.1913-1918:ieee.
[7]w.yuan,s.dong,ande.h.adelson,″gelsight:high-resolutionrobottactilesensorsforestimatinggeometryandforce,″sensors(basel),vol.17,no.12,nov292017.
[8]k.sato,k.kamiyama,n.kawakami,ands.tachi,″finger-shapedgelforee:sensorformeasuringsurfacetractionfieldsforrobotichand,″ieeetranshaptics,vol.3,no.1,pp.37-47,jan-mar2010.
[9]a.hermanis,r.cacurs,andm.greitans,″accclerationandmagneticsensornetworkforshapesensing,″ieeesensorsjournal,vol.16,no.5,pp.1271-1280,2016.
[10]a.hermanisandk.nesenbergs,″gridshapedaccelerometernetworkforsurfaceshaperecognition,″inelectronicsconference(bec),201213thbiennialbaltic,2012,pp.203-206:ieee.
[11]p.mittendorferandg.cheng,″3dsurfacereconstructionforroboticbodypartswithartificialskins,″inintelligentrobotsandsystems(iros),2012ieee/rsjinternationalconferenceon,2012,pp.4505-4510:ieee.
[12]n.saguin-sprynski,l.jouanet,b.lacolle,andl.biard,″surfacesreconstructionviainertialsensorsformonitoring,″inewshm-7theuropeanworkshoponstructuralhealthmonitoring,2014.
[13]y.-l.park,b.-r.chen,andr.j.wood,″designandfabricationofsoftartificialskinusingembeddedmicrochannelsandliquidconductors,″ieeesensorsjoumal,vol.12,no.8,pp.2711-2718,2012.
[14]v.wall,g.
[15]h.-n.li,d.-s.li,andg.-b.song,″recentapplicationsoffiberopticsensorstohealthmonitoringincivilengineering,″engineeringstructures,vol.26,no.11,pp.1647-1657,2004.
[16]g.c.kahandawa,j.epaarachchi,h.wang,andk.lau,″useoffbgsensorsforshminaerospacestructures,″photonicsensors,vol.2,no.3,pp.203-214,2012.
[17]k.o.hillandg.meltz,″fiberbragggratingtechnologyfundamentalsandoverview,″journaloflightwavetechnology,vol.15,no.8,pp.1263-1276,1997.
[18]p.wei,j.liu,z.dai,andm.li,″monitoringtheshapeofsatellitewingframeusingfbgsensorsinhighelectrioncnoise,vacuumand-196℃environment,″ieeetransactionsonindustrialelectronics,vol.64,no.1,pp.691-700,2017.
[19]b.a.childersetal.,″useof3000bragggratingstrainsensorsdistributedonfour8-mopticalfibersduringstaticloadtestsofacompositestructure,″insmartstructuresandmaterials2001:industrialandcommercialapplicationsofsmartstructurestechnologies,2001,vol.4332,pp.133-143:internationalsocietyforopticsandphotonics.
[20]m.amanzadeh,s.m.aminossadatietal.,″recentdevelopmentsinfibreopticshapesensing,″measurement,2018.
[21]s.c.ryuandp.e.dupont,″fbg-basedshapesensingtubesforcontinuumrobots,″inroboticsandautomation(icra),2014ieeeinternationalconferenceon,2014,pp.3531-3537:ieee.
[22]c.shietal.,″shapesensingtechniquesforcontinuumrobotsinminimallyinvasivesurgery:asurvey,″ieeetransactionsonbiomedicalengineering,vol.64,no.8,pp.1665-1678,2017.
[23]a.f.dasilva,a.f.
[24]l.xu,j.ge,j.h.patel,andm.p.fok,″3-dimensionalsoftshapesensorbasedondual-layerorthogonalfiberbragggratingmesh,″inopticalfibercommunicationsconferenceandexhibition(ofc),2017,2017,pp.1-3:ieee.
[25]h.zhang,x.zhu,z.gao,k.liu,andf.jiang,″fiberbragggratingplatestructureshapereconstructionalgorithmbasedonorthogonalcurvenet,″journalofintelligentmaterialsystemsandstructures,vol.27,no.17,pp.2416-2425,2016.
[26]s.rapp,l.-h.kang,u.c.mueller,j.-h.han,andh.baier,″dynamicshapeestimationbymodalapproachusingfiberbragggratingstrainsensors,″insensorsandsmartstructurestechnologiesforcivil,mechanical,andaerospacesystems2007,2007,vol.6529,p.65293e:internationalsocietyforopticsandphotonics.
[27]r.kashyap,fiberbragggratings.2010.
[28]m.kreuzer,″strainmeasurementwithfiberbragggratingsensors,″hbm,darmstadt,s2338-1.0e,2006.
[29]p.moseley,j.m.florez,h.a.sonar,g.agarwal,w.curtin,andj.paik,″modeling,design,anddevelopmentofsoftpneumaticactuatorswithfiniteelementmethod,″advancedengineeringmaterials,vol.18,no.6,pp.978-988,2016.
[30]m.totaro,a.mondini,a.bellacicca,p.milani,andl.beccai,″integratedsimultaneousdetectionoftactileandbendingcuesforsoftrobotics,″softrobotics,2017.
仅为了方便,在一个或多个附图中示出了本发明的具体特征,因为根据本发明,每个特征可以与其他特征组合。本领域技术人员将认识到替代实施例,并且这些实施例旨在包括在权利要求的范围内。因此,以上描述应该被解释为说明性的而非限制本发明的范围。所有此类明显的改变和修改都在所附权利要求的专利范围内。
尽管已经参考其优选实施例具体示出和描述了本发明,本领域技术人员将理解,在不脱离本发明的精神和范围的情况下,可以在形式和细节上做出各种改变。
- 还没有人留言评论。精彩留言会获得点赞!