一种基于二维点阵的矩形参数提取方法与流程

本发明涉及一种基于二维点阵的矩形参数提取方法，属于图像处理领域。

背景技术：

在基于摄像机和图像处理的工件参数测量应用中，往往需要计算矩形物体的长、宽以及旋转角度。此时的输入数据为经过图像边缘检测的二维平面点集，这些离散坐标点分布在实际矩形边界上，并带有随机噪声。为了获取矩形的参数，一般是采用曲线拟合，然后根据四个边的交叉点计算长、宽及旋转角度。但是这种方法存在的最大问题在于点集中的点不属于同一条直线，所以计算复杂，容易产生误差。

技术实现要素：

本发明的目的是提供一种基于二维点阵的矩形参数提取方法。该方案利用矩形在正位情况下，投影集中最大的原理，精确计算出矩形的长、宽及寻转角度。

本发明解决其技术问题所采用的技术方案是：

一种基于二维点阵的矩形参数提取方法，包括二维平面点集f(i)=(xi,yi)，其中xi和yi为离散坐标，xi的取值上限为xmax，yi的取值上限为ymax,包括以下步骤：

（1）建立数组a[m]，b[n]，并初始化为0，其中0≤m≤xmax，0≤n≤ymax；

（2）计算点集f(i)=(xi,yi)中的x最大值xmax和最小值xmin，y的最大值ymax和最小值ymin；

（3）利用点集f(i)=(xi,yi)中的x、y坐标值，对数组a[m]和b[n]进行投票，即a[xi]=a[xi]+1，b[yi]=b[yi]+1；

（4）比较a[m]的最大值，即a[m¹max]；如果m¹max＞(xmax+xmin)/2，则将m>(xmax+xmin)/2的数组a[m]清零；如果m¹max≤(xmax+xmin)/2，则将m≤(xmax+xmin)/2的数组a[m]清零；比较a[m]的最大值，即a[m²max]；计算边长a=|m¹max-m²max|，权重p^x=a[m¹max]+a[m²max]；

（5）比较b[n]的最大值，即b[n¹max]；如果n¹max＞(ymax+ymin)/2，则将n>(ymax+ymin)/2的数组b[n]清零；如果n¹max≤(ymax+ymin)/2，则将n≤(ymax+ymin)/2的数组b[n]清零；比较b[n]的最大值，即b[n²max]；计算边长b=|n¹max-n²max|，权重p^y=b[n¹max]+b[n²max]；

（6）将坐标轴逆时针旋转0.1º，在新坐标系中更新点集f(i)的坐标值，然后返回步骤1，重新计算；当旋转角度达到90º，进入下一个步骤；

（7）比较出p^x+p^y的最大值，对应的a，b以及旋转角度即为矩形参数的长、宽及倾斜角。

本发明的有益效果主要表现在：1、测量精度高，自动化程度好；2、算法稳定，运算速度快。

附图说明

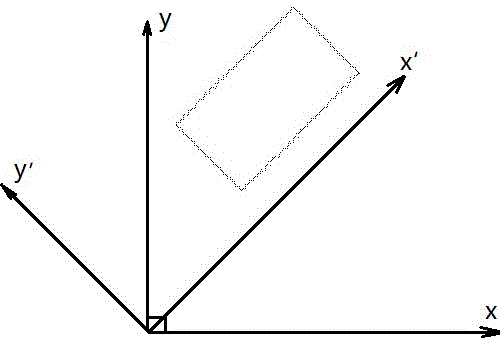
图1是计算示意图。

具体实施方式

下面结合附图对本发明作进一步描述：

参照图1，一种基于二维点阵的矩形参数提取方法，包括二维平面点集f(i)=(xi,yi)，其中xi和yi为离散坐标，xi的取值上限为xmax，yi的取值上限为ymax,xmax和ymax一般为图像的高度值和宽度值。所述的矩形参数提取方法包括以下步骤：

(1)建立数组a[m]，b[n]，并初始化为0，其中0≤m≤xmax，0≤n≤ymax；

(2)计算点集f(i)=(xi,yi)中的x最大值xmax和最小值xmin，y的最大值ymax和最小值ymin；

该步骤可以确定点集f(i)在图像中所处的位置。

(3)利用点集f(i)=(xi,yi)中的x、y坐标值，对数组a[m]和b[n]进行投票，即a[xi]=a[xi]+1，b[yi]=b[yi]+1；

在步骤3中，数组a[m]作为x轴方向上的投票箱，点集f(i)中的每个x坐标值向对应数组单元中投一票；数据b[n]作为y轴方向上的投票箱，点集f(i)中的每个y坐标值向对应数组单元中投一票。如果矩形的边与坐标轴平行或者垂直，则数组a[m]和b[n]会分别出现两个非常突出的峰值，这两个峰值之间的距离就是矩形参数的长或者宽。

(4)比较a[m]的最大值，即a[m¹max]；如果m¹max＞(xmax+xmin)/2，则将m>(xmax+xmin)/2的数组a[m]清零；如果m¹max≤(xmax+xmin)/2，则将m≤(xmax+xmin)/2的数组a[m]清零；比较a[m]的最大值，即a[m²max]；计算边长a=|m¹max-m²max|，权重p^x=a[m¹max]+a[m²max]；

步骤4中，在x轴方向上，根据最大值获得第一个峰值以后，需要清零之后再根据最大值获得第二个峰值。

(5)比较b[n]的最大值，即b[n¹max]；如果n¹max＞(ymax+ymin)/2，则将n>(ymax+ymin)/2的数组b[n]清零；如果n¹max≤(ymax+ymin)/2，则将n≤(ymax+ymin)/2的数组b[n]清零；比较b[n]的最大值，即b[n²max]；计算边长b=|n¹max-n²max|，权重p^y=b[n¹max]+b[n²max]；

步骤5中，在y轴方向上，根据最大值获得第一个峰值以后，需要清零之后再根据最大值获得第二个峰值。

(6)将坐标轴逆时针旋转0.1º，在新坐标系中更新点集f(i)的坐标值，然后返回步骤1，重新计算；当旋转角度达到90º，进入下一个步骤；

因为矩形的边与坐标轴之间可能存在夹角，因此将需要将坐标轴旋转一个非常小的角度，然后返回步骤1进行重新计算。当旋转角度累计达到90时，可以确定矩形与坐标轴存在一个最接近平行或者垂直的计算值，因此结束该步骤。

坐标更新方法可采用坐标旋转公式：xi^t+1=xi^tcos0.1º+yi^tsin0.1º，yi^t+1=yi^tcos0.1º-xi^tsin0.1º。其中，上标t表示当前数据，上标t+1表示更新数据。

(7)比较出p^x+p^y的最大值，对应的a，b以及旋转角度即为矩形参数的长、宽及倾斜角。

p^x+p^y代表矩形的边在x、y轴上投影的集中度，集中度最大的数据则说明矩形的边与坐标轴平行或者垂直，相应的数据就是矩形参数的长、宽及倾斜角。