一种基于卷积混合密度神经网络的短期风速预测方法与流程
本发明涉及短期风速点预测和概率预测的技术领域,尤其是指一种基于卷积混合密度神经网络的短期风速预测方法。
背景技术:
随着保护环境的呼声愈高及常规能源的枯竭,新能源的发展越来越受到大家的关注。其中,作为无污染的可再生能源之一的风能,在全球各地得以大力的开发。风电累积并网装机容量确保达到2.1亿千瓦以上,其中海上风电并网装机量达到500万千瓦以上;风电年发电里确保达到400亿千瓦时,约占全国总发电量的6%。
然而,随着风电穿透力的增加,电力系统的随机性程度不断增强。这给电力系统带来了更多的不确定性,对电力系统的安全、稳定和经济运行构成了更大的威胁。因此,准确的风速预测对提高风能的利用率起着重要的作用。
目前对风速的预测方法主要分为四类:1)物理模型:该模型通过建立风速与温度、湿度、气压、地形等物理量之间的关系实现对风速的预测,主要应用于长期与大范围的风速预测;2)概率统计模型,该模型主要利用统计学的方法,通过历史风速变化预测未来风速;3)空间相关模型,该模型通过考虑不同地点的风速相关性对风速进行预测;4)人工智能模型,该模型使用机器学期、深度学习的方法对未来的风速进行预测。总体而言,现有的风速预测方法对超短期风速预测较为精准,而随着时间长度的增加,预测精度急剧下降。然而,由于火电机组的启停时间受到技术限制,这意味着电网调度员为了确保电网运行的安全,不得不增加电网的备用容量或弃用风电,导致风能利用率降低或者电网运行成本提高;另一方面,随着我国电力市场的建设,由于风速预测不准而带来的电网运行增加的成本必定分摊到用户侧,导致用户用电成本增加。
技术实现要素:
本发明的目的在于克服现有技术的缺点与不足,提出了一种基于卷积混合密度神经网络的短期风速预测方法,突破了传统风速预测方式下预测精度低与预测时间跨度短的问题。本发明利用过去历史风速数据对未来六小时或更长时间的风速均值与标准差进行预测,在延长预测时间跨度的同时提高了预测精度,为调度部门安排机组组合预留了更加充裕的时间,以提高电网运行的稳定性;此外,风速预测的标准差可用于评估风速波动带来的成本,为经济调度带来更多的决策空间。
为实现上述目的,本发明所提供的技术方案为:一种基于卷积混合密度神经网络的短期风速预测方法,包括以下步骤:
1)使用小波变换对原始风速数据进行分解,获得概貌信号与细节信号;
2)对每一层风速信号分别进行归一化处理;
3)将归一化后的历史风速数据送入卷积混合密度神经网络进行学习,用于预测未来时段的风速期望值与标准差;
4)对预测的风速期望与标准差进行反归一化;
5)利用反归一化的预测风速期望值与标准差求取未来时段的风速概率分布。
在步骤1)中,所述小波变化是指使用daubechies母小波将风速原始数据分解成一层代表风速总体变化趋势的概貌信号,与三层代表风速随机性与间歇性的细节信号。
在步骤2)中,对每一层的分解信号,使用泛化的’max-min’归一化方法分别进行归一化处理:
x'max=xmax+0.1×|xmax|
x'min=xmin-0.1×|xmin|
式中,x为小波分解后的每一层数据,xmax为小波分解后的每一层数据的最大值,xmin为小波分解后的每一层数据的最小值,|·|为绝对值,x'max为泛化的最大值,x'min为泛化的最小值,x'是归一化后的数值;
使用泛化的’max-min’归一化方法对每一层风速信号分别进行归一化处理的目的为防止未来数据超出现有数据的数值范围,从而减小极端风速情况下的预测误差。
在步骤3)中,将归一化后的风速数据送入卷积混合密度神经网络进行学习,获得未来q小时风速期望值、标准差与过去p小时原始风速经过小波分解与归一化后数据关系的参数矩阵;其中,所述卷积混合密度神经网络具有以下特点:
a、卷积混合密度神经网络共十层,包括一个输出层、一个输入层与八个隐藏层;在隐藏层中,第一、第六、第七、第八为全连接层,第二与第四层为卷积层,第三与第五层为池化层;每一层均使用relu函数作为激活函数:
式中,a为函数的输入;
每一层在使用激活函数对神经元激活后,均对输出进行批处理,以加快神经网络的训练速度并减小模型的过拟合:
式中,n为批样本的样本数量;xb为批处理的输入,即该层激活函数的输出;yb为批处理的输出,即下一层神经元的输入;μb为批处理中样本各特征的均值,σb为批处理中样本各特征的方差,
b、在输入层中,每一个样本输入xin∈r4×p为小波分解且归一化处理后过去p小时的四层风速信号,每一个样本输出yout∈r2×q为预测的未来q小时的风速期望值与标准差;
c、输出层含有两个神经元,分别用于预测归一化的未来时段风速的期望值与标准差,预测风速期望值的神经元选用sigmoid函数作为激活函数,预测风速标准差的神经元选用变形的elu函数g(a)作为激活函数:
式中,a为函数的输入,exp(·)为指数函数;
理论上,所有输出大于0的函数都能作为预测风速标准差的神经元的激活函数,但已有文献总结变形的elu函数变现最好。
d、卷积混合密度神经网络的损失函数为高斯分布的概率密度函数的负对数:
式中,log(·)为对数函数,pdf为预测的概率分布函数,μ'为预测风速的期望值,σ'为预测风速的标准差,y'为归一化后的真实风速值;通过最小化损失函数,卷积混合密度神经网络对模型中的参数进行学习。
在步骤4)中,使用泛化的极大极小值对预测的风速期望与标准差进行反归一化处理:
y=y'×(z'max-z'min)+z'min
z'max=zmax+0.1×|zmax|
z'min=zmin-0.1×|zmin|
式中,y'为卷积混合密度神经网络的预测数值,zmax为原始风速数据的最大值,zmin为原始风速数据的最小值,|·|为绝对值,z'max为泛化的最大值,z'min为泛化的最小值,y为反归一化的预测数值。
在步骤5)中,通过预测的未来时段的风速期望值与方差,构建未来风速的高斯概率分布:
p(y)~n(μ,σ2)
式中p(y)为预测的风速概率分布,μ为反归一化的预测风速的期望值,σ为反归一化的预测风速的标准差;
通过卷积混合密度神经网络预测获得未来风速的均值与标准差后,使用者可以根据经济性与稳定性的需要,选取不同的显著性水平100(1-α)%,便可以获得不同的风速预测置信区间(μ-z1-α/2σ,μ+z1-α/2σ),从而完成未来风速预测的概率分布,其中z1-α/2为显著性水平100(1-α)%对应的标准分数。
本发明与现有技术相比,具有如下优点与有益效果:
1、本发明使用了卷积神经网络进行风速预测,考虑了不同时间点风速的联系以及风速波动性与概貌风速之间的联系,提高了风速预测的精度,克服了传统风速预测误差大的缺点。
2、本发明实现了对短期风速的预测,在增大风速预测的时间跨度外,还保证了风速预测的精度达到调度的要求。
3、本发明通过使用泛化的归一化方式,避免了极端值带来的预测不稳定性问题,提高了预测模型的泛化性。
4、本发明使用了变形的elu函数作为预测风速标准差的神经元的激活函数,提高了预测精度。
5、本发明方法使用卷积混合密度神经网络对短期风速的期望值与标准差同时进行预测,快速简便实现未来风速概率分布的获取。
6、本发明方法在风速预测中具有广泛的使用空间,操作简单、适应性强,在提高电力系统经济与稳定运行方面有广阔前景。
附图说明
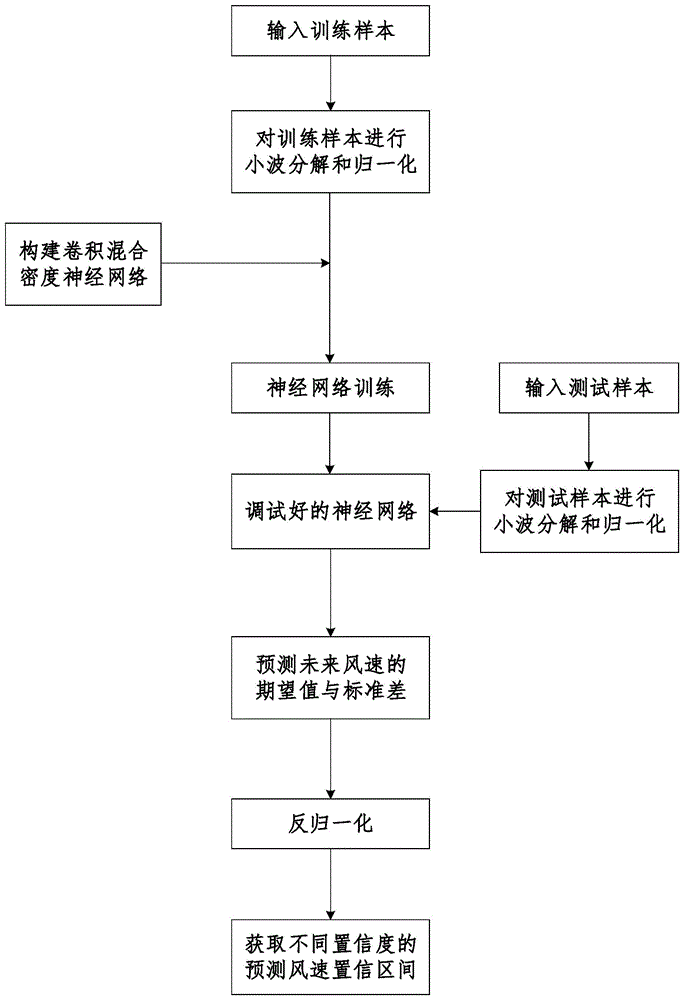
图1为本发明逻辑流程示意图。
图2为本发明使用的卷积混合密度神经网络结构图。
图3为原始风速经过小波分解后的概貌信号与细节信号。
图4a为预测未来一小时风速期望值结果图。
图4b为预测未来两小时风速期望值结果图。
图4c为预测未来三小时风速期望值结果图。
图4d为预测未来四小时风速期望值结果图。
图4e为预测未来五小时风速期望值结果图。
图4f为预测未来六小时风速期望值结果图。
图5a为预测未来一小时风速95%置信区间结果图。
图5b为预测未来两小时风速95%置信区间结果图。
图5c为预测未来三小时风速95%置信区间结果图。
图5d为预测未来四小时风速95%置信区间结果图。
图5e为预测未来五小时风速95%置信区间结果图。
图5f为预测未来六小时风速95%置信区间结果图。
具体实施方式
下面结合具体实施例对本发明作进一步说明。
如图1和图2所示,本实例所提供的基于卷积混合密度神经网络的短期风速预测方法结合了小波分解、卷积神经网络和混合密度网络,包括以下步骤:
1)使用小波变换对原始风速数据进行分解,获得概貌信号与细节信号。
如图3所示,使用daubechies母小波将风速原始数据分解成一层代表风速总体变化趋势的概貌信号,与三层代表风速随机性与间歇性的细节信号。
2)对每一层的分解信号,分别使用泛化的’max-min’归一化方法进行归一化处理:
x'max=xmax+0.1×|xmax|
x'min=xmin-0.1×|xmin|
式中,x为小波分解后的每一层数据,xmax为小波分解后的每一层数据的最大值,xmin为小波分解后的每一层数据的最小值,|·|为绝对值,x'max为泛化的最大值,x'min为泛化的最大值,x'是归一化后的数值;
使用泛化的’max-min’归一化方法对每一层风速信号分别进行归一化处理的目的为防止未来数据超出现有数据的数值范围,从而减小极端风速情况下的预测误差。
3)将归一化后的风速数据送入卷积混合密度神经网络进行学习,获得未来q小时风速期望值、标准差与过去p小时原始风速经过小波分解与归一化后数据关系的参数矩阵,卷积混合密度神经网络具有以下特点:
a、卷积混合密度神经网络共十层,包括一个输出层、一个输入层与八个隐藏层;在隐藏层中,第一、第六、第七、第八为全连接层,第二与第四层为卷积层,第三与第五层为池化层;每一层均使用relu函数作为激活函数:
式中,a为函数的输入;
每一层在使用激活函数对神经元激活后,均对输出进行批处理,以加快神经网络的训练速度并减小模型的过拟合:
式中,n为批样本的样本数量;xb为批处理的输入,即该层激活函数的输出;yb为批处理的输出,即下一层神经元的输入;μb为批处理中样本各特征的均值,σb为批处理中样本各特征的方差,
b、在输入层中,每一个样本输入xin∈r4×p为小波分解且归一化处理后过去p小时的四层风速信号,每一个样本输出yout∈r2×q为预测的未来q小时的风速期望值与标准差;
c、输出层含有两个神经元,分别用于预测归一化的未来时段风速的期望值与标准差,预测风速期望值的神经元选用sigmoid函数作为激活函数,预测风速标准差的神经元选用变形的elu函数g(a)作为激活函数:
式中,a为函数的输入,exp(·)为指数函数;
理论上,所有输出大于0的函数都能作为预测风速标准差的神经元的激活函数,但已有文献总结变形的elu函数变现最好。
d、卷积混合密度神经网络的损失函数为高斯分布的概率密度函数的负对数:
式中,log(·)为对数函数,pdf为预测的概率分布函数,μ'为预测风速的期望值,σ'为预测风速的标准差,y'为归一化后的真实风速值;通过最小化损失函数,卷积混合密度神经网络对模型中的参数进行学习。
4)用泛化的极大极小值对预测的风速期望与标准差进行反归一化处理:
y=y'×(z'max-z'min)+z'min
z'max=zmax+0.1×|zmax|
z'min=zmin-0.1×|zmin|
式中,y'为卷积混合密度神经网络的预测数值,zmax为原始风速数据的最大值,zmin为原始风速数据的最小值,|·|为绝对值,z'max为泛化的最大值,z'min为泛化的最小值,y为反归一化的预测数值。
5)通过预测的未来时段的风速期望值与方差,构建未来风速的高斯概率分布:
p(y)~n(μ,σ2)
式中p(y)为预测的风速概率分布,μ为反归一化的预测风速的期望值,σ为反归一化的预测风速的标准差;
如图4a至图4f、图5a至图5f所示,通过卷积混合密度神经网络预测获得未来风速的均值与标准差后,使用者可以根据经济性与稳定性的需要,选取不同的显著性水平100(1-α)%,便可以获得不同的风速预测置信区间(μ-z1-α/2σ,μ+z1-α/2σ),从而完成未来风速预测的概率分布,其中z1-α/2为显著性水平100(1-α)%对应的标准分数。
综上所述,在采用以上方案后,本发明为短期风速提供了新的预测方法,该方法能够准确预测短期风速期望值与概率分布,具有预测时间跨度长、预测精度高的特点,具有实际推广价值,值得推广。
以上所述实施例只为本发明之较佳实施例,并非以此限制本发明的实施范围,故凡依本发明之形状、原理所作的变化,均应涵盖在本发明的保护范围内。
- 还没有人留言评论。精彩留言会获得点赞!