一种基于黎曼网络的矩阵词典摘要方法与流程

本发明涉及二阶特征，具体是涉及一种基于黎曼网络的矩阵词典摘要方法。

背景技术：

作为典型的二阶特征，对称正定矩阵最近流形于各种计算机视觉和人工智能应用的特征表示中，例如图像分类[1-2]、动作识别[3-4]和脑机接口分析[5]等。对称正定矩阵落在一个锥形的黎曼流形空间内，通过保留这种非欧几何性质，对称正定矩阵特征可以消除欧式空间里膨胀效应带来的影响[6]，在某些特定领域能带来极大的性能提升。

近年来，随着硬件gpu快速发展及大数据时代的来临，深度学习得到了迅猛发展，已席卷人工智能各个领域，包括语音识别、图像识别、视频跟踪、自然语音处理等在内的图、文、视频领域。深度学习技术突破了传统技术方法，大大提高各领域的识别性能。但是大部分相关工作只考虑了一阶统计信息，部分考虑二阶信息的方案仍存在一些问题。如文献[7-8]用协方差作为二阶统计信息来为细粒度分类提供更好的区域描述子，但这种方案没有对二阶特征降维。文献[3]对对称正定矩阵进行了降维，但使用了近似的方法从黎曼空间映射到欧氏空间，由此带来了性能的损失。考虑一种更高效、高性能的二阶特征处理方法将成为研究重点。

参考文献：

[1].fathy,m.e.,andchellappa,r.2017.imagesetclassificationusingsparsebayesianregression.inwacv.

[2].wang,q.；li,p.；andzhang,l.2017.g2denet:globalgaussiandistributionembeddingnetworkanditsapplicationtovisualrecognition.incvpr.

[3].guo,k.；ishwar,p.；andkonrad,j.2013.actionrecognitionfromvideousingfeaturecovariancematrices.tip.

[4].huang,z.,andvangool,l.j.2017.ariemanniannetworkforspdmatrixlearning.inaaai.

[5].lotte,f.；bougrain,l.；cichocki,a.；clerc,m.；congedo,m.；rakotomamonjy,a.；andyger,f.2018.areviewofclassificationalgorithmsforeeg-basedbrain–computerinterfaces:a10yearupdate.journalofneuralengineering.

[6].arsigny,v.；fillard,p.；pennec,x.；andayache,n.2007.geometricmeansinanovelvectorspacestructureonsymmetricpositive-definitematrices.siamjmaa.

[7].lin,t.-y.,andmaji,s.2017.improvedbilinearpoolingwithcnns.inbmvc.

[8].lin,t.-y.；roychowdhury,a.；andmaji,s.2015.bilinearcnnmodelsforfine-grainedvisualrecognition.iniccv.

技术实现要素：

本发明的目的是针对传统基于二阶特征方法难以扩展到深度学习或难以处理好黎曼空间与欧式空间关系的缺点，考虑在黎曼网络的架构下用距离表征向量来过渡空间转换，提供一种基于黎曼网络的矩阵词典摘要方法。

本发明包括以下步骤：

1)对于输入的高维二阶特征，在约束对称正定矩阵的黎曼流形上进行降维处理；

2)在低维空间根据对应类别构建类别相关的词典作为原始高维二阶特征的数据摘要；

3)计算输入特征与摘要数据之间的多种测地线距离关系得到距离向量，即二阶特征的欧式空间表达；

4)对距离向量进行分类。

与现有技术相比，本发明具有以下突出优点：

通过本发明所提出的方案能够获得一个鲁棒、高性能的黎曼特征数据摘要机制，该机制组合了对称正定矩阵降维和分类模块，用基于度量学习方案来压缩整个训练集得到数据摘要的方法，解决了黎曼空间词典学习和网络优化问题。通过采用计算数据特征和摘要数据黎曼距离的方法，将黎曼空间问题转化为欧式空间，方便现有欧式空间方法的使用。整个框架可以同个常规的矩阵反向传播端到端的进行学习，并能达到极高的精度。

附图说明

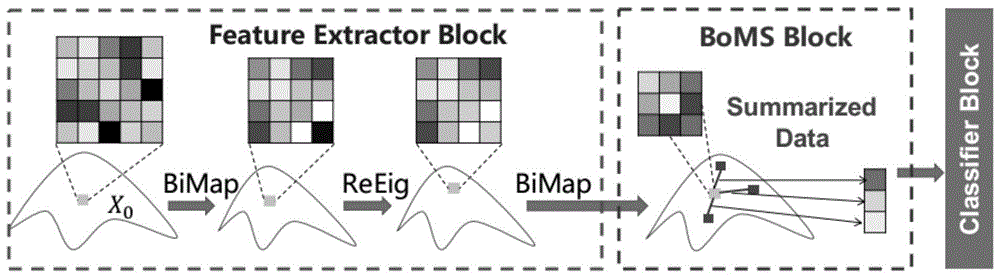
图1为本发明的整体框架图。

具体实施方式

以下实施例将结合附图对本发明作进一步的说明。

本发明的目的是针对传统基于二阶特征方法难以扩展到深度学习或难以处理好黎曼空间与欧式空间关系的缺点，考虑在黎曼网络的架构下用距离表征向量来过渡空间转换，提出一种基于黎曼网络的矩阵词典摘要方法。具体的框架如图1所示。

具体的每个模块如下：

1)二阶特征降维模块

对称正定矩阵落在一个锥形的黎曼流形空间内，因此现有的欧式空间降维方法不能直接应用。为保持非欧几何性质，本发明采用类似spdnet的结构，用多个bimap层和reeig层对高维二阶特征进行降维。

bimap层：

xk＝wkxk-1wk

其中，wk-1为第k层输入，是对称正定矩阵；xk为第k层输出，wk为第k层参数。为保证xk正定，约束wk正交。bimap层主要用于将高维对称正定矩阵转换为低维矩阵。

reeig层：

其中，uk-1和∑k-1通过对xk-1特征值分解得到reeig层主要用于非线性激活。

2)数据摘要模块

数据摘要模块在低维空间学习词典来压缩训练集，输出输入数据与词典间的距离向量用于后续任务。数据摘要模块的输出为：

v＝[d(x，b1)，d(x，b2)，...，d(x，bm)]^t∈r^m

其中，x为低维对称正定矩阵特征，b为词典，d(·，·)为黎曼距离度量。

本发明采用了三种黎曼度量方式：

a)boms-1：d(a，b)＝||log(a)-log(b)||

b)boms-2：d(a，b)＝||wlog(a)-wlog(b)||，其中w为矫正参数，需学习

c)boms-3：d(a，b)＝loq|(a+b)/2|-0.5*log|ab|

为了更好的学习词典，本发明同时约束相同类别的输入到相同类别的词典距离应小于到不同类别的距离；同时，为了防止同类词典收敛到同一点，强制惩罚同类词典距离不应过小。

2)分类模块

对由上文数据摘要模块产生的距离向量进行多分类，通常包含全连接层、softmax层和交叉熵损失函数。

实验结果：

对称正定矩阵特征常用的数据集包括人脸表情数据集afew、动作识别数据集hdm05、脑机接口数据集bci和人脸识别数据集ytc。本发明(boms)与现有方法在精度与时间的对比结果见表1。

表1

由表1可见，本发明在不显著增加时间复杂度的情形下，多种变种均取得高于现有方法的精度。