一种考虑新能源接入的输电网规划方法和系统与流程

本发明涉及电力系统规划领域,并且更具体地，涉及一种考虑新能源接入的输电网规划方法和系统。

背景技术：

随着新能源发电技术的日趋成熟，风能和太阳能发电在电力系统中的占比持续增加。高比例的风力发电和太阳能发电并网将给电力系统带来强不确定性，其中大规模集中式新能源并网将给电源侧带来强不确定性，分布式新能源接入将给负荷侧带来强不确定性，导致负荷更加难以预测。不确定因素的存在使电力系统运行与规划面临极大的挑战。

随着新能源比例的持续增加，网架薄弱是引起弃风、弃光现象的重要原因之一。究其原因，在于电网规划过程中对新能源出力等不确定因素的考虑不够深入。因此，输电网规划过程中要充分考虑新能源出力的不确定性，保证新能源发电的充分利用就成为一个亟需解决的技术问题。

为了增强高比例新能源电力系统的安全性，降低新能源限电率，学者们已经对含高比例新能源的输电网规划方法进行了研究，目前主要有以下几种方法：(1)考虑不确定因素概率模型的含新能源输电网规划方法；(2)考虑不确定因素区间模型的含新能源输电网鲁棒规划方法；(3)基于聚类方法的含新能源输电网多场景规划方法。其中，多场景规划方法仅考虑几种确定的新能源出力场景，可能由于遗漏重要的场景造成规划方案安全性较低。不确定性规划方法均将不确定因素以同一种不确定性数学模型描述，但是在实际电网规划过程中，可能出现由于规划基础信息获取不完全等原因，不确定因素可采用不同的不确定性模型表征，例如新能源出力采用区间模型表征的同时预测负荷采用模糊模型表征等，因此已有输电网规划方法不能满足规划要求。

技术实现要素：

为了解决现有技术中已有输电网规划方法不能满足规划要求的技术问题，本发明提供一种考虑新能源接入的输电网规划方法，所属方法包括：

步骤1、基于预先输入的电网网络数据，建立新能源出力的区间模型以及预测负荷的模糊模型；

步骤2、基于扩展模糊机会约束规划模型，建立考虑所述新能源出力的区间模型和预测负荷的模糊模型的输电网模糊鲁棒规划模型；

步骤3、将所述输电网模糊鲁棒规划模型转化为等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型；

步骤4：基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案，其中，所述算法数据是对所述输电网鲁棒规划模型进行求解时采用的粒子群优化算法中需要设置的参数。

进一步地，所述方法在建立新能源出力的区间模型以及预测负荷的模糊模型之前还包括输入进行输电网规划所需的电网网络数据和算法数据，，其中，所述算法数据是对所述输电网鲁棒规划模型进行求解时采用的粒子群优化算法中需要设置的参数。

进一步地，所述基于预先输入的电网网络数据，建立新能源出力的区间模型以及预测负荷的模糊模型，其中：

所述新能源出力的区间模型的表达式为：

式中，表示新能源出力，表示新能源出力的上限，即新能源发电额定容量；

所述预测负荷的模糊模型的表达式为：

式中，μ(d)表示预测负荷的模糊隶属度函数，dl、dm和dh分别表示负荷预测低、中、高三种场景的负荷值，为表述方便，所述表达式(2)记为d～[dl,dm,dh]。

进一步地，所述基于扩展模糊机会约束规划模型，建立考虑所述新能源出力的区间模型和预测负荷的模糊模型的输电网模糊鲁棒规划模型，所述输电网模糊鲁棒规划模型的表达式为：

nij是整数变量(8)

n-1(9)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；γij表示支路ij一条线路的电纳；表示支路ij原有线路条数；ωl表示支路集合；cr{·}表示可信性测度算子，β表示可信度指标；表示支路ij的潮流上限；表示发电机出力上限列向量；表示支路ij新增线路数的上限；式(3)为输电网模糊鲁棒规划模型的目标函数，表示线路投资成本的最小化；式(4)表示节点功率平衡约束；式(5)表示支路ij潮流方程约束；式(6)表示支路潮流不越限可信性约束，物理意义为在新能源出力取其区间内任意值时，由负荷的模糊性导致的模糊支路潮流，其不越限的可信度大于某预先设定的置信水平；式(7)表示发电机出力约束；式(8)表示支路新增线路约束；式(9)表示n-1约束，即单一元件故障情况下满足约束式(4)至式(7)。

进一步地，所述将所述输电网模糊鲁棒规划模型转化为等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型，其中，所述等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型表达式为：

nij是整数变量(16)

n-1(17)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；ωl表示支路集合；β表示可信度指标；表示发电机出力上限列向量；表示支路ij新增线路数的上限，μd(·)表示模糊负荷的隶属度函数，在输电网鲁棒规划模型中，将输电网模糊鲁棒规划模型中的模糊负荷模型转化为区间负荷模型，即该规划模型中不确定因素数学模型只含有区间模型，降低了不确定性的维度，式(14)表示区间负荷的范围对应原模糊负荷模型的2(1-β)水平截集。

进一步地，所述基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案包括：

步骤1、设置迭代次数计数器k＝0；

步骤2、产生第k代规划方案，即在n维搜索空间中，第i个粒子的位置信息和速度信息分别由xi＝{xi1,xi2,…,xin}和vi＝{vi1,vi2,…,vin}表示，令和分别为到第k次迭代时第i个粒子的个体最优方案和粒子群体的全局最优方案，每个粒子的位置信息和速度信息进行更新的公式为：

式中，vi^k和分别是第k次迭代中第i个粒子的速度信息和位置信息，ω是惯性权重因子，c1和c2是加速系数，r1和r2是[0,1]之间的随机数，其中，所述位置信息代表生成的规划方案，所述速度信息代表相邻两次迭代过程中规划方案的变化情况，所述ω、c1、c2、r1、r2均为预先输入的算法数据；

当k＝0时，令vi^k＝0，随机产生；

步骤3、通过改进分支定界法得到的区间最小切负荷值以及模型的目标函数获得规划方案的适应度值，所述规划方案的适应度值公式为：

式中，ff(·)表示规划方案的适应度值；表示通过粒子群算法得到的第k代第m个规划方案；m表示一个很大的数；lshed表示由改进分支定界法得到的规划方案区间最小切负荷值；

步骤4、更新个体最优方案和全局最优方案，其中，所述更新个体最优方案和全局最优方案的公式为：

步骤5、令迭代次数计数器k＝k+1；

步骤6、当所述迭代次数计数器k达到预先设置的最大值时，或者当所述迭代次数计数器k小于预先设置的最大值，且全局最优方案连续迭代n次依然保持不变时，输出全局最优方案作为输电网最优规划方案，否则，转到步骤2，其中，所述迭代次数最大值和全局最优方案保持不变的次数n为预先输入的算法数据。

根据本发明的另一方面，本发明提供一种考虑新能源接入的输电网规划系统，所属系统包括：

第一模型单元，其用于基于预先输入的电网网络数据，建立新能源出力的区间模型以及预测负荷的模糊模型；

第二模型单元，其用于基于扩展模糊机会约束规划模型，建立考虑所述新能源出力的区间模型和预测负荷的模糊模型的输电网模糊鲁棒规划模型；

第三模型单元，其用于将所述输电网模糊鲁棒规划模型转化为等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型；

最佳方案单元，其用于基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案，其中，所述算法数据是对所述输电网鲁棒规划模型进行求解时采用的粒子群优化算法中需要设置的参数。

进一步地，所述系统还包括参数输入单元，其用于在第一模型单元建立新能源出力的区间模型以及预测负荷的模糊模型之前输入进行输电网规划所需的电网网络数据和算法数据。

进一步地，所述第一模型单元包括：

新能源出力单元，其用于建立新能源出力的区间模型，所述模型的表达式为：

式中，表示新能源出力，表示新能源出力的上限，即新能源发电额定容量；

预测负荷单元，其用于建立预测负荷的模糊模型，所述模型的表达式为：

式中，μ(d)表示预测负荷的模糊隶属度函数，dl、dm和dh分别表示负荷预测低、中、高三种场景的负荷值，为表述方便，所述表达式(2)记为d～[dl,dm,dh]。

进一步地，所述第二模型单元的输电网模糊鲁棒规划模型的表达式为：

nij是整数变量(8)

n-1(9)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；γij表示支路ij一条线路的电纳；表示支路ij原有线路条数；ωl表示支路集合；cr{·}表示可信性测度算子，β表示可信度指标；表示支路ij的潮流上限；表示发电机出力上限列向量；表示支路ij新增线路数的上限；式(3)为输电网模糊鲁棒规划模型的目标函数，表示线路投资成本的最小化；式(4)表示节点功率平衡约束；式(5)表示支路ij潮流方程约束；式(6)表示支路潮流不越限可信性约束，物理意义为在新能源出力取其区间内任意值时，由负荷的模糊性导致的模糊支路潮流，其不越限的可信度大于某预先设定的置信水平；式(7)表示发电机出力约束；式(8)表示支路新增线路约束；式(9)表示n-1约束，即单一元件故障情况下满足约束式(4)至式(7)。

进一步地，所述第三模型单元的等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型表达式为：

nij是整数变量(16)

n-1(17)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；ωl表示支路集合；β表示可信度指标；表示发电机出力上限列向量；表示支路ij新增线路数的上限，μd(·)表示模糊负荷的隶属度函数，在输电网鲁棒规划模型中，将输电网模糊鲁棒规划模型中的模糊负荷模型转化为区间负荷模型，即该规划模型中不确定因素数学模型只含有区间模型，降低了不确定性的维度，式(14)表示区间负荷的范围对应原模糊负荷模型的2(1-β)水平截集。

进一步地，所述最优方案单元基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案包括：

步骤1、设置迭代次数计数器k＝0；

步骤2、产生第k代规划方案，即在n维搜索空间中，第i个粒子的位置信息和速度信息分别由xi＝{xi1,xi2,…,xin}和vi＝{vi1,vi2,…,vin}表示，令和分别为到第k次迭代时第i个粒子的个体最优方案和粒子群体的全局最优方案，每个粒子的位置信息和速度信息进行更新的公式为：

式中，vi^k和分别是第k次迭代中第i个粒子的速度信息和位置信息，ω是惯性权重因子，c1和c2是加速系数，r1和r2是[0,1]之间的随机数，其中，所述位置信息代表生成的规划方案，所述速度信息代表相邻两次迭代过程中规划方案的变化情况，所述ω、c1、c2、r1、r2均为预先输入的算法数据；

当k＝0时，令vi^k＝0，随机产生；

步骤3、通过改进分支定界法得到的区间最小切负荷值以及模型的目标函数获得规划方案的适应度值，所述规划方案的适应度值公式为：

式中，ff(·)表示规划方案的适应度值；表示通过粒子群算法得到的第k代第m个规划方案；m表示一个很大的数；lshed表示由改进分支定界法得到的规划方案区间最小切负荷值；

步骤4、更新个体最优方案和全局最优方案，其中，所述更新个体最优方案和全局最优方案的公式为：

步骤5、令迭代次数计数器k＝k+1；

步骤6、当所述迭代次数计数器k达到预先设置的最大值时，或者当所述迭代次数计数器k小于预先设置的最大值，且全局最优方案连续迭代n次依然保持不变时，输出全局最优方案作为输电网最优规划方案，否则，转到步骤2，其中，所述迭代次数最大值和全局最优方案保持不变的次数n为预先输入的算法数据。

本发明技术方案提供的考虑新能源接入的输电网规划方法和系统基于扩展的模糊机会约束规划方法，提出了同时考虑新能源出力区间模型和预测负荷模糊模型的输电网模糊鲁棒规划方法，并给出其等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型，最后采用粒子群算法对所述输电网鲁棒规划模型进行求解，将输出的全局最优方案作为有新能源接入的输电网的最佳规划方案。本发明所述的考虑新能源接入的输电网规划方法和系统采用考虑多种不确定因素区间模型和模糊模型的输电网模糊鲁棒规划方法，相比于仅考虑一种不确定因素数学模型的规划方法，对含高比例新能源输电网规划的适应性大大加强；而且相比于仅考虑新能源出力区间模型的输电网鲁棒规划方法，本发明在不增加计算量的前提下，可以获得协调经济性和安全性的含新能源输电网划方案，避免了鲁棒规划方法的保守性。

附图说明

通过参考下面的附图，可以更为完整地理解本发明的示例性实施方式：

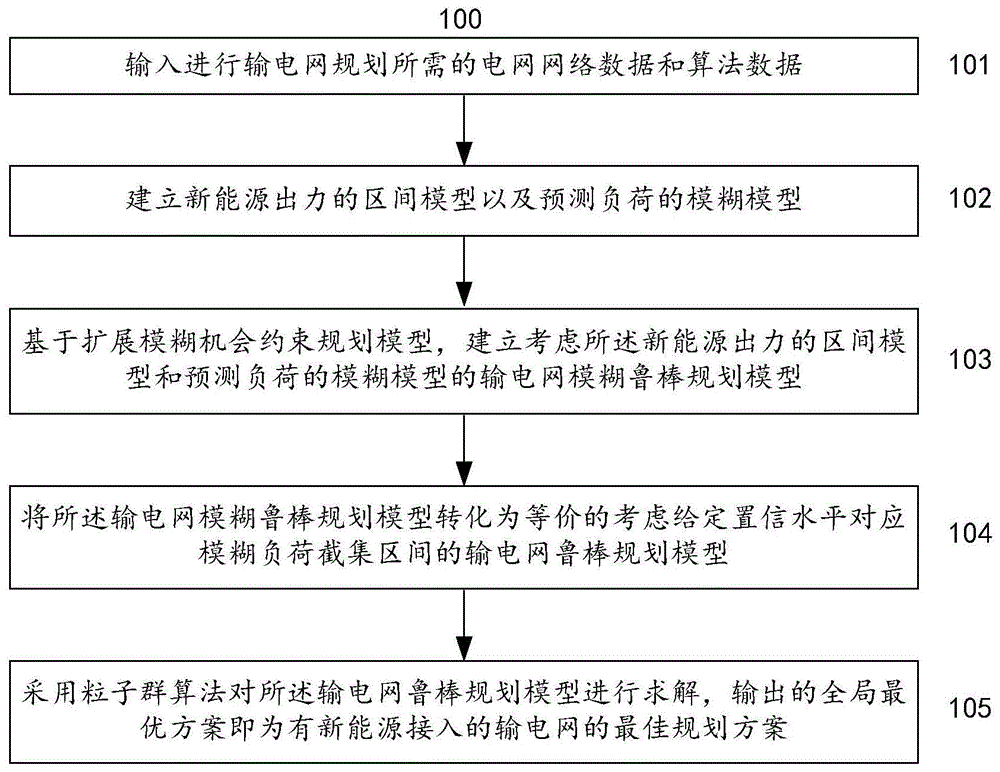
图1为根据本发明优选实施方式的考虑新能源接入的输电网规划的方法的流程图；

图2为根据本发明优选实施方式的输电网规划方案示意图；

图3为根据本发明优选实施方式的考虑新能源接入的输电网规划系统的结构示意图。

具体实施方式

现在参考附图介绍本发明的示例性实施方式，然而，本发明可以用许多不同的形式来实施，并且不局限于此处描述的实施例，提供这些实施例是为了详尽地且完全地公开本发明，并且向所属技术领域的技术人员充分传达本发明的范围。对于表示在附图中的示例性实施方式中的术语并不是对本发明的限定。在附图中，相同的单元/元件使用相同的附图标记。

除非另有说明，此处使用的术语(包括科技术语)对所属技术领域的技术人员具有通常的理解含义。另外，可以理解的是，以通常使用的词典限定的术语，应当被理解为与其相关领域的语境具有一致的含义，而不应该被理解为理想化的或过于正式的意义。

图1为根据本发明优选实施方式的考虑新能源接入的输电网规划的方法的流程图。如图1所示，本优选实施方式所述的考虑新能源接入的输电网规划方法100从步骤101开始。

在步骤101，输入进行输电网规划所需的电网网络数据和算法数据，其中，所述算法数据是对所述输电网鲁棒规划模型进行求解时采用的粒子群优化算法中需要设置的参数。

在步骤102，基于预先输入的电网网络数据，建立新能源出力的区间模型以及预测负荷的模糊模型。

优选地，所述基于预先输入的电网网络数据，建立新能源出力的区间模型以及预测负荷的模糊模型，其中：

所述新能源出力的区间模型的表达式为：

式中，表示新能源出力，表示新能源出力的上限，即新能源发电额定容量；

所述预测负荷的模糊模型的表达式为：

式中，μ(d)表示预测负荷的模糊隶属度函数，dl、dm和dh分别表示负荷预测低、中、高三种场景的负荷值，为表述方便，所述表达式(2)记为d～[dl,dm,dh]。

在步骤103，基于扩展模糊机会约束规划模型，建立考虑所述新能源出力的区间模型和预测负荷的模糊模型的输电网模糊鲁棒规划模型。

所述的扩展模糊机会约束规划模型的表达式为：

minf(x,ξ,ζ)

s.t.cr{gj(x,ξ,ζ)<0}>β,j＝1,…,p

式中，x为决策向量，ξ为模糊参数向量，ζ为区间参数向量，f(x,ξ,ζ)为目标函数，gj(x,ξ,ζ)<0，j＝1,2,…,p为约束条件，约束条件表示无论ζ取其区间范围内任意值，模糊机会约束条件均满足；由于约束中融入了模糊变量，因此希望该约束以一定的可信度水平β成立，即需要满足模糊机会约束：cr{gj(x,ξ,ζ)<0}>β，其中cr{·}表示可信性测度算子，所述cr{·}的表达式为：

cr{·}＝0.5×(pos{·}+nec{·})

式中，pos{·}表示事件发生的可能性；nec{·}表示事件发生的必要性。

在本优选实施方式中，所述基于扩展模糊机会约束规划模型，建立考虑所述新能源出力的区间模型和预测负荷的模糊模型的输电网模糊鲁棒规划模型，所述输电网模糊鲁棒规划模型的表达式为：

nij是整数变量(8)

n-1(9)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；γij表示支路ij一条线路的电纳；表示支路ij原有线路条数；ωl表示支路集合；cr{·}表示可信性测度算子，β表示可信度指标；表示支路ij的潮流上限；表示发电机出力上限列向量；表示支路ij新增线路数的上限；式(3)为输电网模糊鲁棒规划模型的目标函数，表示线路投资成本的最小化；式(4)表示节点功率平衡约束；式(5)表示支路ij潮流方程约束；式(6)表示支路潮流不越限可信性约束，物理意义为在新能源出力取其区间内任意值时，由负荷的模糊性导致的模糊支路潮流，其不越限的可信度大于某预先设定的置信水平；式(7)表示发电机出力约束；式(8)表示支路新增线路约束；式(9)表示n-1约束，即单一元件故障情况下满足约束式(4)至式(7)。

在步骤104，将所述输电网模糊鲁棒规划模型转化为等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型。

优选地，所述将所述输电网模糊鲁棒规划模型转化为等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型，其中，所述等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型表达式为：

nij是整数变量(16)

n-1(17)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；ωl表示支路集合；β表示可信度指标；表示发电机出力上限列向量；表示支路ij新增线路数的上限，μd(·)表示模糊负荷的隶属度函数，在输电网鲁棒规划模型中，将输电网模糊鲁棒规划模型中的模糊负荷模型转化为区间负荷模型，即该规划模型中不确定因素数学模型只含有区间模型，降低了不确定性的维度，式(14)表示区间负荷的范围对应原模糊负荷模型的2(1-β)水平截集。

式(3)至(9)称为模型①，式(10)至(17)称为模型②，下面给出模型①和模型②等价性的证明：

定理1：模型②的可行域是模型①的可行域，即满足规划模型②约束的可行规划方案均可满足预测负荷模糊模型下系统可信性测度大于等于β的要求。

从两个模型的对比可以看出，唯一的不同点为模型①中预测负荷的不确定性以模糊模型表征，而模型②中预测负荷的不确定性以区间模型表征。在多维可再生能源出力构成的空间内任意选择一个元素(即多维可再生能源出力的一个样本)，如果可以证明区间负荷下系统的安全性满足模糊负荷下潮流不越限的可信性测度大于等于β这一条件，就说明模型②的可行域属于模型①的可行域。

证明：令集合a为满足安全约束的负荷集合，集合a^c为不满足安全约束的负荷集合。求解模型②得到的规划方案可满足模糊负荷在2(1-β)截集对应的区间内取值时系统的安全性要求，由于2(1-β)截集对应的取值区间内包含了隶属度为1的负荷值，因此pos{a}＝1。在2(1-β)截集对应的取值区间外，所有负荷状态可能性的最大值小于2(1-β)，因此对于不满足系统安全要求的负荷集合a^c，其可能性pos{a^c}≤2(1-β)。因此可以得到cr{a}＝0.5×(pos{a}+nec{a})＝0.5×(pos{a}+1-pos{a^c})≥β，即集合a中元素满足系统潮流不越限的可信度水平至少为β，也就是系统安全性的可信性水平要大于等于β，即满足模型①中的所有约束。因此模型②的可行域是模型①的可行解，进而定理1得证。

定理2：模型①的可行域是模型②的可行域，即满足模型①约束的可行规划方案均可满足负荷在2(1-β)截集对应的区间内取值时系统的安全性要求。

如前所述两个模型的不同点为模型①中预测负荷的不确定性以模糊模型表征，而模型②中预测负荷的不确定性以区间模型表征。因此在多维可再生能源出力构成的空间内任意选择一个元素(即多维可再生能源出力的一个样本)，如果可以证明模糊负荷下潮流不越限的可信性测度大于等于β满足区间负荷下系统的安全性这一条件，就说明模型①的可行域属于模型②的可行域。

证明：定理2采用反证法进行证明。若规划方案可信度指标大于或等于β，但此时模糊负荷在其2(1-β)截集对应的区间内取值时，存在不满足系统安全性的负荷，即系统会出现切负荷，根据区间最小切负荷模型的负荷边界特性，系统切负荷量的上限必定在区间负荷的边界处达到。因此系统必定在负荷取值为2(1-β)截集对应的区间边界上存在切负荷，即不满足系统安全性要求。这样，有pos{a^c}≥2(1-β)，由pos{a}＝1(若cr{a}≥0.5，必有pos{a}＝1)，可得cr{a}＝0.5×(pos{a}+nec{a})＝0.5×(pos{a}+1-pos{a^c})<β。由于定理2前提条件是规划方案满足约束式(8)中可信性测度大于等于β的要求，因此所得到的结论同前提条件矛盾，即假设不成立。故满足模型①约束的规划方案均可满足负荷在2(1-β)截集对应区间内取值时系统的安全性要求，即满足模型②的约束。因此，定理2得证。

定理1和定理2表明，规划模型①的可行域和规划模型②的可行域是一致的。此外，两个输电网规划模型均以最小化投资成本为目标，因此求解两个模型得到的最优规划方案也是相同的，即求解模型①等价于求解模型②。模型①求解过程中需采用模糊蒙特卡洛模拟和改进分支定界的双重计算来确定规划方案的安全性，复杂程度高，计算量大。而模型②求解过程中仅采用改进分支定界法来确定规划方案的安全性，计算量较小。

在步骤105，基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案，其中，所述算法数据是对所述输电网鲁棒规划模型进行求解时采用的粒子群优化算法中需要设置的参数。

优选地，所述基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案包括：

步骤1、设置迭代次数计数器k＝0；

步骤2、产生第k代规划方案，即在n维搜索空间中，第i个粒子的位置信息和速度信息分别由xi＝{xi1,xi2,…,xin}和vi＝{vi1,vi2,…,vin}表示，令和分别为到第k次迭代时第i个粒子的个体最优方案和粒子群体的全局最优方案，每个粒子的位置信息和速度信息进行更新的公式为：

式中，vi^k和分别是第k次迭代中第i个粒子的速度信息和位置信息，ω是惯性权重因子，c1和c2是加速系数，r1和r2是[0,1]之间的随机数，其中，所述位置信息代表生成的规划方案，所述速度信息代表相邻两次迭代过程中规划方案的变化情况，所述ω、c1、c2、r1、r2均为预先输入的算法数据；

当k＝0时，令vi^k＝0，随机产生；

步骤3、通过改进分支定界法得到的区间最小切负荷值以及模型的目标函数获得规划方案的适应度值，所述规划方案的适应度值公式为：

式中，ff(·)表示规划方案的适应度值；表示通过粒子群算法得到的第k代第m个规划方案；m表示一个很大的数；lshed表示由改进分支定界法得到的规划方案区间最小切负荷值；

步骤4、更新个体最优方案和全局最优方案，其中，所述更新个体最优方案和全局最优方案的公式为：

步骤5、令迭代次数计数器k＝k+1；

步骤6、当所述迭代次数计数器k达到预先设置的最大值时，或者当所述迭代次数计数器k小于预先设置的最大值，且全局最优方案连续迭代n次依然保持不变时，输出全局最优方案作为输电网最优规划方案，否则，转到步骤2，其中，所述迭代次数最大值和全局最优方案保持不变的次数n为预先输入的算法数据。

图2为根据本发明优选实施方式的输电网规划方案示意图。如图2所示，在ieeerts24节点系统中，一共有34条现存的输电走廊，41条候选支路，每条候选支路最大可添加3条线路。假设有3座风电场分别接入节点7、节点16和节点22，风电场容量分别为300mw、900mw和900mw，风电场出力模型采用区间不确定性模型。节点预测负荷值如表1所示。

表1修改的ieee24节点系统负荷参数

假定每个节点的预测负荷d的模糊隶属度函数都为三角模糊数且隶属度函数具体分布为[0.9d,d,1.1d]。粒子群算法的种群为50，最大迭代次数设置为200。针对等价后的模型分别求解了给定置信水平β为0.75和0.85情况下的规划方案，针对原规划模型求解了置信水平为0.85情况下的规划方案，具体规划方案如表2所示。表2中第二列给出了规划的前提条件(可信性测度β)。第三列内容为根据规划模型等价定理得出的指定可信性测度下每个节点预测负荷的等效区间范围，对于本算例给出的模糊隶属度函数，通过计算可知其在2(1-β)截集处对应的等价负荷区间范围为[1.1-0.2β,0.9+0.2β]。

表2给定置信水平下的24节点规划方案

对比方案1和方案2可知，方案2的成本大于方案1的成本，这是由于方案2支路潮流不越限的可信性测度大于方案1支路潮流不越限的可信性测度，即方案2的安全性高于方案1的安全性；通过对比方案2和方案3可知，求解原模型和等价后的模型得到的规划方案是一致的，说明了本文所提规划方法的正确性。

图3为根据本发明优选实施方式的考虑新能源接入的输电网规划系统的结构示意图。如图3所示，本优选实施方式所述的考虑新能源接入的输电网规划系统300包括：

参数输入单元301，其用于在第一模型单元建立新能源出力的区间模型以及预测负荷的模糊模型之前输入进行输电网规划所需的电网网络数据和算法数据。

第一模型单元302，其用于基于预先输入的电网网络数据，建立新能源出力的区间模型以及预测负荷的模糊模型；

第二模型单元303，其用于基于扩展模糊机会约束规划模型，建立考虑所述新能源出力的区间模型和预测负荷的模糊模型的输电网模糊鲁棒规划模型；

第三模型单元304，其用于将所述输电网模糊鲁棒规划模型转化为等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型；

最佳方案单元305，其用于基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案，其中，所述算法数据是对所述输电网鲁棒规划模型进行求解时采用的粒子群优化算法中需要设置的参数。

优选地，所述第一模型单元302包括：

新能源出力单元321，其用于建立新能源出力的区间模型，所述模型的表达式为：

式中，表示新能源出力，表示新能源出力的上限，即新能源发电额定容量；

预测负荷单元322，其用于建立预测负荷的模糊模型，所述模型的表达式为：

式中，μ(d)表示预测负荷的模糊隶属度函数，dl、dm和dh分别表示负荷预测低、中、高三种场景的负荷值，为表述方便，所述表达式(2)记为d～[dl,dm,dh]。

优选地，所述第二模型单元303的输电网模糊鲁棒规划模型的表达式为：

nij是整数变量(8)

n-1(9)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；γij表示支路ij一条线路的电纳；表示支路ij原有线路条数；ωl表示支路集合；cr{·}表示可信性测度算子，β表示可信度指标；表示支路ij的潮流上限；表示发电机出力上限列向量；表示支路ij新增线路数的上限；式(5)为输电网模糊鲁棒规划模型的目标函数，表示线路投资成本的最小化；式(6)表示节点功率平衡约束；式(7)表示支路ij潮流方程约束；式(8)表示支路潮流不越限可信性约束，物理意义为在新能源出力取其区间内任意值时，由负荷的模糊性导致的模糊支路潮流，其不越限的可信度大于某预先设定的置信水平；式(9)表示发电机出力约束；式(10)表示支路新增线路约束；式(11)表示n-1约束，即单一元件故障情况下满足约束式(6)至式(9)。

优选地，所述第三模型单元304的等价的考虑给定置信水平对应模糊负荷截集区间的输电网鲁棒规划模型表达式为：

nij是整数变量(16)

n-1(17)

式中，cij表示支路ij新增一条线路的成本，nij表示支路新增线路数；b表示节点导纳矩阵的虚部；表示节点相角列向量；表示发电机出力列向量；表示可再生能源出力列向量；表示预测负荷列向量；表示支路ij的潮流；ωl表示支路集合；β表示可信度指标；表示发电机出力上限列向量；表示支路ij新增线路数的上限，μd(·)表示模糊负荷的隶属度函数，在输电网鲁棒规划模型中，将输电网模糊鲁棒规划模型中的模糊负荷模型转化为区间负荷模型，即该规划模型中不确定因素数学模型只含有区间模型，降低了不确定性的维度，式(14)表示区间负荷的范围对应原模糊负荷模型的2(1-β)水平截集。

优选地，所述最优方案单元305基于预先输入的算法数据，采用粒子群算法对所述输电网鲁棒规划模型进行求解，输出的全局最优方案即为有新能源接入的输电网的最佳规划方案包括：

步骤1、设置迭代次数计数器k＝0；

步骤2、产生第k代规划方案，即在n维搜索空间中，第i个粒子的位置信息和速度信息分别由xi＝{xi1,xi2,…,xin}和vi＝{vi1,vi2,…,vin}表示，令和分别为到第k次迭代时第i个粒子的个体最优方案和粒子群体的全局最优方案，每个粒子的位置信息和速度信息进行更新的公式为：

式中，vi^k和分别是第k次迭代中第i个粒子的速度信息和位置信息，ω是惯性权重因子，c1和c2是加速系数，r1和r2是[0,1]之间的随机数，其中，所述位置信息代表生成的规划方案，所述速度信息代表相邻两次迭代过程中规划方案的变化情况，所述ω、c1、c2、r1、r2均为预先输入的算法数据；

当k＝0时，令vi^k＝0，随机产生；

步骤3、通过改进分支定界法得到的区间最小切负荷值以及模型的目标函数获得规划方案的适应度值，所述规划方案的适应度值公式为：

式中，ff(·)表示规划方案的适应度值；表示通过粒子群算法得到的第k代第m个规划方案；m表示一个很大的数；lshed表示由改进分支定界法得到的规划方案区间最小切负荷值；

步骤4、更新个体最优方案和全局最优方案，其中，所述更新个体最优方案和全局最优方案的公式为：

步骤5、令迭代次数计数器k＝k+1；

步骤6、当所述迭代次数计数器k达到预先设置的最大值时，或者当所述迭代次数计数器k小于预先设置的最大值，且全局最优方案连续迭代n次依然保持不变时，输出全局最优方案作为输电网最优规划方案，否则，转到步骤2，其中，所述迭代次数最大值和全局最优方案保持不变的次数n为预先输入的算法数据。

本发明所述考虑新能源接入的输电网规划系统对有新能源接入的输电网进行规划的方法与本发明所述考虑新能源接入的输电网规划方法的步骤相同，并且达到的技术效果也相同，此处不再赘述。

已经通过参考少量实施方式描述了本发明。然而，本领域技术人员所公知的，正如附带的专利权利要求所限定的，除了本发明以上公开的其他的实施例等同地落在本发明的范围内。

通常地，在权利要求中使用的所有术语都根据他们在技术领域的通常含义被解释，除非在其中被另外明确地定义。所有的参考“一个/所述/该[装置、组件等]”都被开放地解释为所述装置、组件等中的至少一个实例，除非另外明确地说明。这里公开的任何方法的步骤都没必要以公开的准确的顺序运行，除非明确地说明。