一种高精度多重同步压缩广义S变换时频分析方法与流程

本发明属于通信信号处理的技术领域，具体涉及一种高精度多重同步压缩广义s变换时频分析方法。

背景技术：

时频分析作为处理非平稳信号领域的一个重要分支，一直是现代信号处理的研究热点之一。时频分析方法提供了时间域与频率域的联合分布信息，清楚地描述了信号频率随时间变化的关系。常用的时频分析方法有短时傅里叶变换(stft)、小波变换(cwt)、s变换(st)及广义s变换(gst)等。其中，短时傅里叶变换窗函数的“大小”和“形状”是保持不变的，所以得到的时频谱的时频分辨率处处相同。小波变换通过信号的时间-尺度进行分析，可达到多分辨率的特点，但其本质上还是一种基于平稳信号、窗口可调的傅里叶变换，并且小波函数的选取直接决定了小波变换分析的效果，从而限制了对信号的精细分析。s变换时窗的宽度可自适应地与频率成反比变化，既克服了短时傅里叶变换不能调节时窗长度的缺点，又解决了小波变换的相位局部化问题，但由于s变换采用的时窗函数形状固定，这在一定程度上限制了s变换的应用。为此，广义s变换在小波变换和s变换的基础上进行了改进，它通过参数调节得到更加灵活多变的窗函数，在应用中具有更高的实用性和灵活性，但因受heisenberg-gabor不定问题影响，其时频谱分辨率仍不能达到最优。

2018年，于刚等人提出了多重同步压缩变换(msst)，此方法是在短时傅里叶变换的基础上提出的一种新的时频变换方法。msst首先通过严格的数学推导将短时傅里叶变换结果在一定频率范围内的时频能量“挤压”到信号的中心频率附近，得到同步压缩变换(sst)的结果；紧接着对sst结果继续进行多次同步压缩操作，其中每次同步压缩后的时频谱能量聚集性都有所提升，进而达到提高时频分辨率的目的。

msst的实质是在原始瞬时频率估计值的基础上采用一种逐步逼近信号真实瞬时频率的迭代算法，定义了多重瞬时频率估计值，随着重数的增加，瞬时频率估计越准确，进而使得msst后的时频谱能量聚集性越强，以此提高了时频分辨率。同时msst是基于stft的后处理步骤，因此短时傅里叶变换的时频特征将不可避免地影响着经过“压缩”的结果。所以原始线性时频方法时频分辨率的高低对多重同步压缩变换方法的时频分辨率至关重要。

技术实现要素：

本发明的目的在于针对现有技术中的上述不足，提供一种高精度多重同步压缩广义s变换时频分析方法，以解决或改善上述的问题。

为达到上述目的，本发明采取的技术方案是：

一种高精度多重同步压缩广义s变换时频分析方法，其包括：

s1、输入待分析的原始一维信号x(t)；

s2、对输入信号x(t)进行三参数广义s变换，得到广义s变换值gst(f,τ)，并对所述广义s变换值求模得到广义s变换的时频谱|gst(f,τ)|；

gst(f,τ)的计算方法如下：

其中，f为频率，t为时间，τ为时间轴位移参数，j为虚数单位，λ和p为窗函数调节因子，m是s变换和短时傅里叶变换之间的权重因子；

s3、根据所述广义s变换值，得到时频面上各点瞬时频率的初步估计值；

s4、根据上述瞬时频率估计值通过n次迭代计算得到时频面上各点更为精确的n重瞬时频率估计值；

s5、以时频谱上频率集合为中心频率集合，把每一中心频率附近区间内的瞬时频率对应的时频点值挤压到所述中心频率点，得到n重同步压缩广义s变换值；

s6、对所述n重同步压缩广义s变换值进行求模，得到n重同步压缩广义s变换的时频谱。

优选地，步骤s3中得到时频面上各点瞬时频率的初步估计值fx(f,τ)为：

其中，是偏导符号。

优选地，步骤s4中n重瞬时频率估计值为：

当n＝1时，

即一重瞬时频率估计值即为所述步骤s3中得到的瞬时频率的初步估计值。

优选地，步骤s5中得到的n重同步压缩广义s变换值ts^[n](τ,η)为：

本发明提供的高精度多重同步压缩广义s变换时频分析方法，具有以下有益效果：

本发明的多重同步压缩广义s变换相比于广义s变换，多重同步压缩广义s变换通过对广义s变换时频谱上信号瞬时频率高精度的多重估计，而后通过“压缩”操作，使信号的真实瞬时频率得以凸显，且更加精细，在广义s变换的基础上极大地提高了信号的时间和频率分辨率。

附图说明

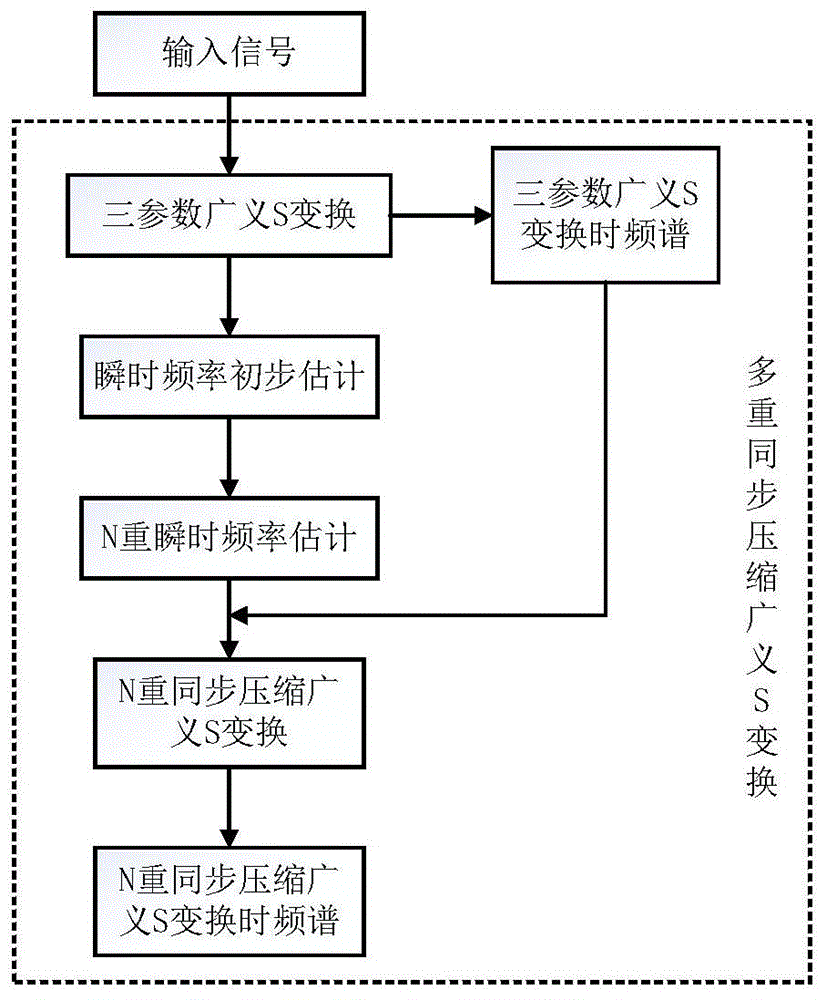
图1为高精度多重同步压缩广义s变换时频分析方法的流程图。

图2为合成信号。

图3为对合成信号进行短时傅里叶变换得到的时频谱。

图4为对合成信号进行三参数广义s变换得到的时频谱。

图5为对合成信号进行一重同步压缩广义s变换得到的时频谱。

图6为对合成信号进行六重同步压缩变换(msst)得到的时频谱。

图7为对合成信号进行六重同步压缩广义s变换得到的时频谱。

图8为图5、图6、图7中灰色矩形框部分的放大图。

具体实施方式

下面对本发明的具体实施方式进行描述，以便于本技术领域的技术人员理解本发明，但应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。

根据本申请的一个实施例，参考图1，本方案的高精度多重同步压缩广义s变换时频分析方法，包括：

s1、输入待分析的原始一维信号x(t)；

s2、对输入信号x(t)进行三参数广义s变换，得到广义s变换值gst(f,τ)，并对所述广义s变换值求模得到广义s变换的时频谱|gst(f,τ)|；

gst(f,τ)的计算方法如下：

其中，f为频率，t为时间，τ为时间轴位移参数，j为虚数单位，λ和p为窗函数调节因子，m是s变换和短时傅里叶变换之间的权重因子。

s3、根据所述广义s变换值，得到时频面上各点瞬时频率的初步估计值fx(f,τ)；

fx(f,τ)的具体计算方法为：

其中，是偏导符号。

s4、根据上述瞬时频率估计值通过n次迭代计算得到时频面上各点更为精确的n重瞬时频率估计值

的计算表达式为：

特别地，当n＝1时，

这说明一重瞬时频率估计值即为所述步骤s3中得到的瞬时频率的初步估计值。

s5、以时频谱上频率集合为中心频率集合，把每一中心频率附近区间内的瞬时频率对应的时频点值挤压到所述中心频率点，得到n重同步压缩广义s变换值ts^[n](τ,η)；

ts^[n](τ,η)的计算方法如下：

s6、对所述n重同步压缩广义s变换值ts^[n](τ,η)进行求模，得到n重同步压缩广义s变换的时频谱|ts^[n](τ,η)|。

本发明以多重同步压缩变换与广义s变换为基础，结合了多重同步压缩变换和广义s变换的优点，具有更高的时频分解精度。

多重同步压缩广义s变换有别于多重同步压缩变换，从多重同步压缩变换与多重同步压缩广义s变换算法本质上分析两者效果不同的原因，多重同步压缩变换是基于短时傅里叶变换结果的，因此短时傅里叶变换的时频特征将不可避免地影响着最后经“压缩”后的结果。

多重同步压缩广义s变换是基于广义s变换的结果，由于广义s变换可通过调整控制其窗口函数的参数改变窗口函数的形态，使结果具有类似小波变换的多分辨率特征，从而使得多重同步压缩广义s变换结果不但具有较好时频分辨率，而且具有较强的灵活性。

多重同步压缩广义s变换相比于广义s变换，多重同步压缩广义s变换通过对广义s变换时频谱上信号瞬时频率高精度的多重估计，而后通过“压缩”操作，使信号的真实瞬时频率得以凸显，且更加精细，在广义s变换的基础上极大地提高了信号的时间和频率分辨率。

根据本申请的一个实施例，合成信号是检验时频分布的时频聚焦性能好坏的公认模型，采用图2展示的合成信号来进行试验。

通过对图3、图4、图5、图6、图7进行对比分析发现，短时傅里叶变换时频谱的信号能量模态混叠严重，在真实瞬时频率附近存在一定宽度的伪频率成分，分辨率有限。

相比之下，广义s变换的时频谱模态混叠程度有所减轻；同步压缩广义s变换时频谱虽相比较好，但仍有明显的模糊现象；多重同步压缩变换以及多重同步压缩广义s变换的时频谱都呈现出了较好的时频聚焦性。

观察图8可以发现，相比多重同步压缩变换时频谱，多重同步压缩广义s变换时频谱的频率分辨率更好，能更好地减少交叉项的干扰，且处理更精细。

虽然结合附图对发明的具体实施方式进行了详细地描述，但不应理解为对本专利的保护范围的限定。在权利要求书所描述的范围内，本领域技术人员不经创造性劳动即可做出的各种修改和变形仍属本专利的保护范围。