一种水产养殖溶解氧预测方法与流程

本发明属于水产养殖技术领域，尤其是一种水产养殖溶解氧预测方法。

背景技术：

水产养殖的水域是养殖鱼类的生活环境，养殖环境的好坏直接关系到养殖鱼类的生长和发育，从而决定着水产品质量和产量的高低。近年来，随着水产养殖规模化、集约化程度的不断提高，养殖种类的增多和养殖密度的增加，养殖水域环境日益恶化，病害发生率越来越高，由此引发水产品质量安全问题也日益突出。

溶解氧是水产品生存的重要指标，对其实现实时、精准的控制显得极为重要。精准预测是提供可靠控制的前提，若对溶解氧的预测发生错误，增氧机工作不及时，其浓度过低或过高都会给水产品带来危害，对用户造成巨大的损失，甚至影响水产养殖生态环境的健康可持续发展。因此，建立准确实时的预测系统对于水产养殖中溶解氧的控制是非常必要的。

目前，针对溶解氧的预测方法过于单一，操作人员仍然凭借工作经验对溶解氧进行控制，没有深入参考空气湿度、光照条件、水温、ph值等其他水产养殖环境因子的影响。这些影响因子间的关系非常复杂，对于溶解氧数值的影响也不同，很难建立一个综合多因子的多维度、高精度的预测模型。

技术实现要素：

本发明的目的在于克服现有技术的不足，提出一种水产养殖溶解氧预测方法，解决现有水产养殖中溶解氧预测精度低、输入维度单一的问题。

本发明解决其技术问题是采取以下技术方案实现的：

一种水产养殖溶解氧预测方法，包括以下步骤：

步骤1、采用遗传算法优化支持向量回归机模型，对支持向量回归机模型中的参数进行全局寻优，得到基于遗传算法的支持向量回归机模型；

步骤2、将多维度数据代入基于遗传算法的支持向量回归机模型进行训练，实现多维数据的输入、溶解氧预测值的输出；

步骤3、利用马尔科夫链对预测结果的残差进行矫正，建立最终溶解氧预测模型，并对测试集中的数据进行溶解氧参数预测。

进一步，所述步骤1对支持向量回归机模型中的参数进行全局寻优的方法为：

⑴设置遗传算法参数：种群规模、迭代次数、交叉概率和变异概率；

⑵染色体编码：对待优化参数设置变化区间并进行编码；

⑶种群生成：随机生成第一代种群，并获得第一代染色体；

⑷模型训练：将生成的染色体代入支持向量回归机模型，对训练集数据进行训练，获得支持向量回归机模型的训练结果；

⑸采用如下适应度函数计算适应度：

式中，n为样本数，yi为真实值，预测输出；f为染色体的适应度值；

⑹判断是否满足条件：当个体适应度小于目标适应度或迭代次数到达目标值，则退出循环生成基本预测模型；若未满足条件则进入步骤⑺。

⑺进行选择运算、交叉运算和遗传运算，生成下一代种群，进入步骤⑷继续处理。

进一步，所述步骤⑺的具体实现方法为：

①选择运算的方法为：根据适应度值的大小，淘汰一些较差的个体，选出一些比较优良的个体；

②所述交叉运算的方法为：两个染色体的部分结构加以替换重组而生成新个体的操作；若一对染色体被确定进行交叉操作，则需要确定一个或多个交叉点；交叉算子采用单点实数交叉法，不同染色体在对应的某个位置上以概率pcross进行交叉操作，pcross一般取值在[0.4,0.99]之间；

③遗传运算：变异的概率pmut取较小的值，并在[0.0001,0.1]区间内选择。

进一步，所述步骤3的具体实现方法为：

⑴基于遗传算法的支持向量回归机模型预测：针对训练集中的数据进行溶解氧参数预测，获取初步的预测结果；

⑵计算残差并归一化处理：将基于遗传算法的支持向量回归机模型的预测结果与溶解氧实际值作差，获得溶解氧预测的残差，并采用下式进行归一化处理：

式中，x为基于遗传算法的支持向量回归机模型的预测值，xmin为预测值中的最小值，xmax为预测值中的最大值，为归一化后的预测值；

⑶状态划分：得到残差区间后，将残差区间平均划分为三个子区间，分别为状态区间s1、状态区间s2、状态区间s3；

⑷计算1步和k步状态转移概率矩阵：根据划分后的状态区间，对残差数据进行整理获得markov状态转移矩阵，根据状态转移矩阵获得1步状态转移概率矩阵，最终计算出k步状态转移概率矩阵；

⑸残差修正：根据初始残差状态向量p0和k步状态转移概率矩阵获得k步残差的状态向量，根据概率判断第k步残差的状态区间，并根据下式对残差进行处理：

式中：为归一化后的预测值，qmin为第k步残差状态区间下限，qmax为第k步残差状态区间上限，x为经残差修正后预测值；

⑹对测试集数据进行预测：经过以上步骤，获得最终溶解氧预测模型并利用该预测模型对测试集中的数据进行溶解氧参数预测。

进一步，所述多维度数据包括溶解氧、水温、ph值、降雨量、太阳辐射、风速和湿度。

本发明的优点和积极效果是：

本发明采用遗传算法优化支持向量回归机模型并对模型中的参数进行全局寻优，利用马尔科夫链实现对于预测结果的残差矫正功能，从而建立精确的溶解氧预测模型，同时，利用多维度的水质影响因子预测溶解氧，提高了溶解氧预测的精度，实现了溶解氧预测的实时性。

附图说明

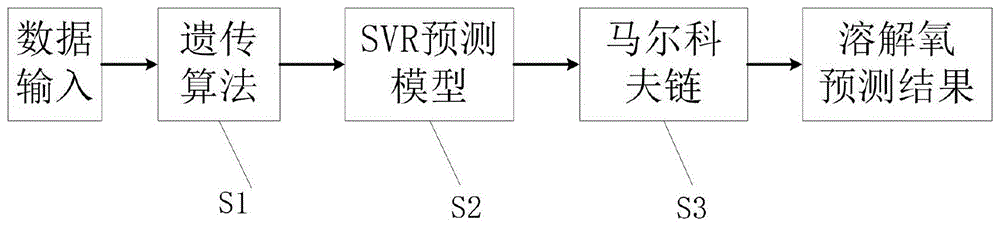
图1是本发明的整体处理流程图；

图2是采用ga优化svr预测模型结构框图；

图3是采用马尔科夫链模型优化预测模型结构框图。

具体实施方式

以下结合附图对本发明实施例做进一步详述。

本发明的设计思想是：采用基于遗传算法和马尔科夫链优化的支持向量回归机模型，用以实现对水产养殖中溶解氧的预测。采用的技术包括支持向量回归机模型(svr)、遗传算法(ga)和马尔科夫链模型。所述支持向量回归机模型用于建立多维度溶解氧预测的核心预测模型，所述遗传算法用于更加准确地确定支持向量回归机中个各个参数，所述马尔科夫链模型用于修正预测结果中出现的残差，提高预测模型的精度。

基于上述设计思想，本发明的一种水产养殖溶解氧预测方法，如图1所示，包括以下步骤：

步骤1、采用遗传算法(ga)优化支持向量回归机模型(svr)，针对svr模型中的参数进行全局寻优，得到基于遗传算法的支持向量回归机模型(ga-svr模型)。具体方法如下：

本发明采用支持向量回归机预测模型，其通过建立训练数据中的待预测参数和支持向量间的非线性关系，对测试数据的待预测参数进行预测。svr通过内积核函数定义的非线性变换将输入的数据转换到高维特征空间中，并在高维空间中回归，计算式为：

f(x)＝w·φ(x)+b(1)

式中：φ(x)为核函数；w为权重系数；b为偏置项。根据结构风险最小化原则，权重系数w与偏差b可通过最小化得到如下目标函数：

式中：|f(xi)-yi|ε为损失函数。||w||²为欧拉范数。

为使欧拉范数最小，也使超出精度的拟合误差得到控制，引入松弛变量和则式(2)中的最优化问题可转化为约束最小化问题，即：

式中：c为惩罚因子，ε为不敏感参数。

为导出原始式(3)的对偶问题，引入拉格朗日乘子αi,α*i,ηi,即可建立原始问题的拉格朗日方程。分别对拉格朗日方程中的w,b,ξi,求偏导数，并使偏导数的值为零。将结果代入拉格朗日方程中，即可得到原始问题的对偶问题：

由此，将原始问题转换为了凸二次规划问题。通过求解该二次规划问题，即可最终得到支持向量机回归模型：

其中，核函数采用rbf核函数：

k(xi,x)＝exp(-γ||xi-x||²)(6)

为了确定svr模型中的如下三个系数：宽度系数γ、惩罚系数c、不敏感损失系数ε，使用遗传算法(ga)作为最优参数搜索算法。如图2所示，具体实现方法如下：

s101，ga参数设置：设置ga算法的种群规模、迭代次数、交叉概率和变异概率。

s102，染色体编码：染色体为待优化参数，染色体编码即对待优化参数设置变化区间并进行编码，便于ga处理数据，常用的有二进制法，实数法等。

s103，种群生成：ga算法初始化完毕后，随机生成第一代种群，并获得第一代染色体。

s104，svr模型训练：将生成的染色体代入svr模型，对训练集数据进行训练，获得svr模型训练结果。

s105，计算适应度：适应度函数是衡量优化参数优劣的指标。根据个体得到的参数，用训练数据对svr进行训练，并预测其输出，把预测输出和期望输出之间的误差绝对值之和作为个体的适应度值。计算公式如下：

式中n为样本数，yi为真实值，预测输出；f为染色体的适应度值。

s106，判断是否满足条件：当个体适应度小于目标适应度或迭代次数到达目标值即为满足退出循环条件，则退出循环生成ga-svr模型；若未满足条件则继续下列遗传算法的过程。

s107，选择、交叉、遗传运算：

(1)选择运算：选择操作用于模拟自然界优胜略汰的自然选择过程。为了确保进化过程朝着优化的方向进行，选择过程根据求得的适应度值的大小，淘汰一些较差的个体，选出一些比较优良的个体。

(2)交叉运算：交叉操作相当于的是生物遗传基因的重组，本质是为了增强算法的全局搜索能力。所谓交叉是把两个染色体的部分结构加以替换重组而生成新个体的操作。若一对染色体被确定进行交叉操作，则需要确定一个或多个交叉点。由于染色体采用实数编码，因此，本专利选择的交叉算子是单点实数交叉法，即不同染色体在对应的某个位置上以概率pcross进行交叉操作，pcross一般取值在[0.4,0.99]之间。

(3)遗传运算：变异操作的本质是增强算法的局部搜索能力，避免陷入局部极小值，同时维持种群的多样性，以防止过早收敛。因此，变异的概率pmut应取较小的值，通常在[0.0001,0.1]区间内选择。

种群经过选择、交叉、遗传运算后，生成下一代种群，继续第s104步流程。

步骤2，将溶解氧、水温、ph值、降雨量、太阳辐射、风速和湿度参数代入基于遗传算法的支持向量回归机模型进行训练，实现多维数据的输入、溶解氧预测值的输出。

步骤3、利用马尔科夫链实现对于预测结果的残差矫正，建立ga-svr-markov预测模型，对测试集中的数据进行溶解氧参数预测，从而提高溶解氧预测模型的预测精度。

如图3所示，本步骤的具体实现方法如下：

s301，ga优化svr模型预测：根据svr训练模型，针对训练集中的数据进行溶解氧参数预测，获取初步的预测结果。

s302，计算残差并归一化处理：将svr模型的预测结果与溶解氧实际值作差，获得溶解氧预测误差，即残差。并对残差进行归一化处理。归一化处理计算式为：

式中，x为基于遗传算法的支持向量回归机模型的预测值，xmin为预测值中的最小值，xmax为预测值中的最大值，为归一化后的预测值；

s303，状态划分：得到残差区间后，将残差区间平均划分为三个子区间，分别为状态区间s1、状态区间s2、状态区间s3。

s304，计算1步和k步状态转移概率矩阵：根据划分后的状态区间，对残差数据进行整理获得markov状态转移矩阵，根据状态转移矩阵获得1步状态转移概率矩阵，最终计算出k步状态转移概率矩阵。

s305，残差修正：根据初始残差状态向量p0和k步状态转移概率矩阵获得k步残差的状态向量，根据概率判断第k步残差的状态区间，并根据式(9)对残差进行处理。

式中：为ga-svr模型的预测值，qmin为第k步残差状态区间下限，qmax为第k步残差状态区间上限，x为经残差修正后预测值。

s306，基于ga-svr-markov预测模型对测试集数据进行预测：经过以上步骤，最终获得ga-svr-markov预测模型，并利用该模型对测试集中的数据进行溶解氧参数预测。

本发明未述及之处适用于现有技术。

需要强调的是，本发明所述的实施例是说明性的，而不是限定性的，因此本发明包括并不限于具体实施方式中所述的实施例，凡是由本领域技术人员根据本发明的技术方案得出的其他实施方式，同样属于本发明保护的范围。