一种火工品可靠性指标的小样本验证方法与流程

本发明属于可靠性指标验证技术领域，尤其涉及一种火工品可靠性指标的小样本验证方法。

背景技术：

火工品是敏感性产品，其可靠性指标较高，一般是通过gjb376-1987规定的计数法试验验证，试验样本量较高。估计值保守，试验量大。当火工品可靠度要求0.999时，常常由于试验量太大，工程上无法实施。如在置信水平0.90、可靠度指标0.999的条件下，需要试验2303发无一失效才能满足技术指标要求。此时，一般采用计量法，如gjb377-94规定的火工品感度试验方法，该方法包括升降法、兰利法、ostr法、步进法等。计量法的优点是使用了产品感度分布模型的信息，所需的试验量较少，其缺点是特征量参数估计的偏差和分布模型的选择错误，会造成可靠度估计较大的误差，且这些方法只能用于推断或预计火工品的可靠性，不能通过试验验证。gjg377a/94提出了火工品感度试验方法，利用感度分布模型推断火工品的可靠性，但由于现有的升降法、兰利法以及d优化法等感度试验方法中，对感度分布均值的估计是无偏的，对感度分布刻度参数的估计是有偏的，因此这种推断方法误差较大，且无法做试验验证，严格来讲并不能用于评估可靠度，只能用于预计。二十世纪九十年代初，美国人提出了“neyerd－最优化法”，该方法也是一种计量法，用于推断感度分布刻度参数时误差较大。

gjb6478-2008给出了一种火工品小样本计数—计量综合评估方法，试验样本量降低约9/10，但该方法也需要使用感度分布均值和刻度参数的估计值，虽然该方法使用的是纠编后的感度分布刻度参数的估计值，但是纠偏后的刻度参数的估计值也不是真值，所以不能保证对可靠度评估结果的准确性。

技术实现要素：

有鉴于此，本发明提供一种火工品可靠性指标的小样本验证方法，只需使用火工品的感度分布均值就能验证火工品的可靠性指标，克服了目前需要根据均值和标准差进行可靠度评估的不足。

为实现上述目的，本发明的火工品可靠性指标的小样本验证方法，包括如下步骤：

步骤1，确定感度分布均值μ；

步骤2，利用零失效条件下的二项分布以及感度分布均值μ下的感度分布计算工作刺激量对应的两个可靠度置信下限的方程；

步骤3，联立两个可靠度置信下限的方程，得到由工作刺激量和对应试验样本量表达的感度分布参数标准差的置限上限σu的方程；

步骤4，保持置信水平一致，将工作刺激量x0和对应试验样本量n，以及工作刺激量x1和对应试验样本量n1分别带入置限上限σu的方程，得到σu的两个方程；其中工作刺激量x0为技术指标规定的工作刺激量，x1为小样本验证对应的工作刺激量，x1＜x0；

联立σu的两个方程，得到工作刺激量x1与对应试验样本量n1的关系式；

步骤5，在工作刺激量x1处进行n1发试验，根据试验结果对火工品可靠性作出判定，若n1发全发火则可靠度满足指标要求，否则不满足。

其中，所述步骤1中，根据工程经验和产品历史数据，进行一组升降法试验、兰利法或d优化法试验，根据感度分布类型，利用极大似然原理估计出感度分布均值μ。

其中，所述步骤2和步骤3中，所述感度分布为正态分布、对数正态分布或逻辑斯谛分布。

有益效果：

本发明提出了一种只需使用感度分布均值的火工品可靠性指标小样本验证方法，综合了计量法和计数法的试验信息，在保持置信水平不变的前提下，大幅度地降低了试验样本量，减少推断误差，提高了可靠度评估结果的准确性。

附图说明

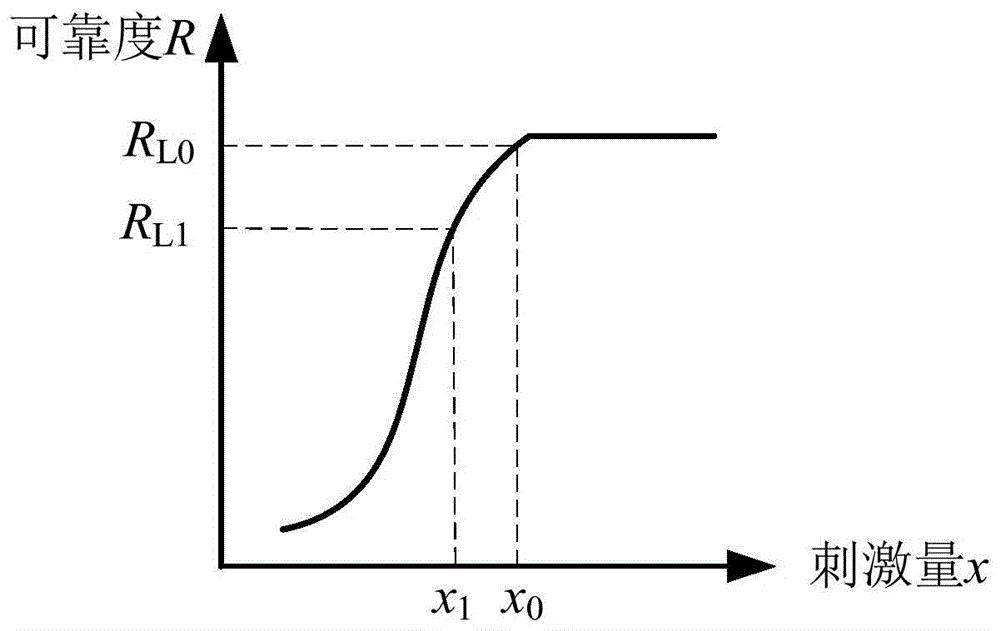
图1为不同刺激量下的可靠度曲线示意图。

具体实施方式

下面结合附图并举实施例，对本发明进行详细描述。

本发明提供一种火工品可靠性指标的小样本验证方法，包括如下步骤：

步骤1，根据工程经验和产品历史数据，进行一组升降法试验、兰利法或d优化法试验，根据感度分布类型，利用极大似然原理估计出感度分布均值μ。

步骤2，在技术指标规定的工作刺激量x0下，利用二项分布在零失效条件下，计算可靠度置信下限rl0的方程：

rl0＝(1-γ)^1/n(1)

其中，γ为置信度，n为试验样本量。

在技术指标规定的工作刺激量x0下，利用感度分布计算可靠度置信下限rl0的方程如下：

当火工品感度分布服从正态分布时

当火工品感度分布服从对数正态分布时

当火工品感度分布服从逻辑斯谛分布时

在工作刺激量x1下，x1＜x0，保持与技术指标规定的置信水平一致，利用二项分布在零失效条件下，计算可靠度置信下限rl1的方程：

其中，n1为工作刺激量x1下的试验样本量；

在工作刺激量x1下，利用感度分布计算可靠度置信下限rl1的方程如下：

当感度分布服从正态分布时

当感度分布服从对数正态分布时

当感度分布服从逻辑斯谛分布时

步骤3，联立可靠度置信下限rl0的两个方程，得到由工作刺激量x0表达的感度分布参数标准差的置限上限σu，具体如下：

当感度分布服从正态度分布时：

当感度分布服从对数正态度分布时：

当感度分布服从逻辑斯谛分布时：

联立可靠度置信下限rl1的两个方程，得到由工作刺激量x1表达的感度分布参数标准差的置限上限σu，具体如下：

当感度分布服从正态度分布时：

当感度分布服从对数正态度分布时：

当感度分布服从逻辑斯谛分布时：

由步骤2和步骤3的结果可知，工作刺激量x0和对应的样本量以及工作刺激量x1和对应的样本量是采用同样的方式进行计算的，可见置限上限σu只与工作刺激量和对应试验样本量有关，因此可以采用小样本量以及对应的工作刺激量来代替技术指标要求的工作刺激量和对应试验样本量进行可靠性验证。

可以先得到由工作刺激量和对应试验样本量表达的感度分布参数标准差的置限上限σu的方程，然后再将工作刺激量x0和对应试验样本量n，以及工作刺激量x1和对应试验样本量n1分别带入置限上限σu的方程，得到由工作刺激量x0表达以及由工作刺激量x1表达的感度分布参数标准差的置限上限σu的方程。

步骤4，联立由工作刺激量x0表达以及由工作刺激量x1表达的感度分布参数标准差的置限上限σu的方程，得到试验样本量n1处工作刺激量x1的表达式，或工作刺激量x1处的试验样本量n1的表达式；

根据感度分布类型，分别联立(5)和(12)、(6)和(13)、(7)和(14)，建立低工作刺激量x1和试验样本量的关系，计算试验样本量，具体如下：

当感度分布类型服从正态分布时：

当感度分布类型服从对数正态分布时：

当感度分布类型服从逻辑斯谛分布时：

步骤5，在工作刺激量x1处进行n1发试验，根据试验结果对火工品可靠性作出判定，若n1发全发火则可靠度满足指标要求，否则不满足。

本发明的试验验证1：

空8号电雷管可靠性指标要求：可靠性发火上限700ma，可靠性指标γ＝0.95,r＝0.999。

(1)用本小样本验证方法进行可靠性评估的程序如下：

根据产品历史数据，进行一组升降法试验，试验数据列于表1。

表1升降法试验数据

根据经验，电火工品的感度多属逻辑斯谛分布，因此确定空8号电雷管的感度为逻辑斯谛分布。利用极大似然估计原理求出感度分布均值：

μ＝347.6ma

根据感度分布模型，利用式(20)计算，在工作刺激量xl1＝492.7ma处进行50发试验，若全发火则验证在工作刺激量处满足可靠性指标要求。

在492.7ma处试验产品50发，全部发火，判定该产品发火可靠性达到了置信度γ＝0.95，可靠度r＝0.999的指标。

(2)大样本步进法试验

按gjb/z377a-94进行步进法试验,试验时调节电流作为工作刺激量，单位为ma，工作刺激量最小值取280ma，工作刺激量最大值取400a，工作刺激量步长取15ma，每个工作刺激量点试验200发，共进行9个工作刺激量下的发火试验，总试验样本量1800发。试验时给产品通以规定的直流电流，统计每个工作刺激量下的发火数，试验数据见表2所示。

表2空8号电雷管步进法试验数据统计

χ²检验确定感度分布模型，检验结果见表3所示。

表3空8号电雷管χ²检验结果

从表3得知，四种火工品常见分布假设有三种通过χ²检验，但在相同条件下，根据逻辑斯谛分布假设计算得到的χ²最小，判定空8号电雷管最接近服从逻辑斯谛分布。

在逻辑斯谛分布下，在该火工品的发火可靠度对应工作刺激量的置信上限估计值为：

由于该火工品实际发火上限为700ma，其发火上限估计值小于700ma，则可判断发火上限可靠度达到了r＝0.999的要求，评估结果与小样本方法一致。

本发明的试验验证2：54号针刺雷管可靠度指标为：γ＝0.90，r＝0.999。发火上限为落高6cm，落锤52±1g。

(1)用本发明的小样本方法进行可靠性评估的程序如下：

根据产品历史数据，进行一组升降法试验，试验数据列于表4。

表4升降法试验数据

根据经验,机械类工品的感度多属对数正态分布，因此确定54号针刺雷管的感度为对数正态分布。利用极大似然估计原理求出感度分布均值：

μ＝0.731

根据感度分布模型，利用式(18)计算，在工作刺激量xl1＝5.86cm处进行100发试验，若全发火则验证在工作刺激量处满足可靠性指标要求。

在5.86cm处试验产品100发，全部发火，判定该产品发火可靠性达到了置信度γ＝0.90，可靠度r＝0.999的指标。

(2)大样本步进法试验

按gjb/z377a-94进行步进法试验,落锤重52±1g，试验时用调节落高作为工作刺激量，单位为cm，工作刺激量最小值取1cm，工作刺激量最大值取4.5cm，工作刺激量步长取0.5cm，除在最小工作刺激量下试验400发外，其余的每个工作刺激量下试验200发，共进行8个工作刺激量下的发火试验，总试验样本量1800发。试验时统计每个工作刺激量下的发火数，试验数据见表5所示。

表554号针刺雷管步进法试验数据统计

χ²检验确定感度分布模型,检验结果见表6所示。

表654号针刺雷管χ²检验结果

从表6得知，四种火工品常见分布假设中只有对数正态分布能通过检验，因此可判定54号针刺雷管感度分布最接近服从正态分布。

在对数正态分布下，在该火工品的发火可靠度对应工作刺激量的置信上限估计值为：

由于实际给定的发火上限为6cm，其发火上限估计值小于6cm，则可判断发火上限可靠度达到了r＝0.999的要求，评估结果与小样本方法一致。

可见，本发明方法对于评估可靠度为0.999的产品，低工作刺激量处的试验量在置信水平为0.90或0.95时，机械类火工品取100发，电火工品取50发，加上一组升降法试验或兰利法试验，试验样本量不超过150发，再加上振动、锤击、高温、低温、温度冲击等环境试验60发，至多需要210发产品，比经典统计方法降低了9/10以上。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。