一种复杂机电系统寿命预测方法与流程

本文发明涉及复杂机电系统寿命预测领域，具体涉及一种复杂机电系统寿命预测方法。

背景技术：

复杂机电系统一般指结构复杂，集机、电、液和控制于一体的大型动力装备。随着科技进步，现代生产的规模不断扩大，复杂机电系统作为装备制造业的核心，其安全性可靠性问题限制了行业发展。由于设备的成本问题，完全更换系统需要耗费大量的人力物力，同时工厂停工期间也伴随着大量的经济损失。因此，合理预测系统寿命对提高系统安全性可靠性，减少经济损失具有重要意义。

现有寿命预测研究的方法主要可以分为基于机理模型和数据驱动的方法。基于机理模型的方法是建立失效机理或损伤原理的数学模型来描述系统或者元部件的性能退化过程。基于数据驱动的方法是以概率统计理论为基础，通过建立基于经验知识的统计模型或随机模型，求解得到剩余寿命的概率分布，以量化剩余寿命预测结果的不确定性。而由于系统结构复杂，其机理模型难以获取，因此数据驱动的方法被广泛应用。

而目前寿命预测的对象多为单一系统组件/部件的寿命预测。系统级的预测多是由部件级到系统级，先对系统各部件进行寿命预测，再利用copula函数得到系统的寿命预测模型。而如何处理各部件之间的耦合关系成为建立系统寿命预测模型的主要难点。

技术实现要素：

有鉴于此，本发明的目的在于提出一种复杂机电系统的寿命预测方法。本方法通过经验小波变换对待测信号进行特征提取，再针对系统部件之间的耦合关系建立系统petri网模型，以达到系统寿命预测的目的。

为达到上述目的，本发明的技术方案提供一种复杂机电系统寿命预测方法，所述方法包括以下步骤：

1)对系统构建部件节点统计模型，确定系统的关键部件，实现系统的降维处理。关键部件定义为：各关键部件节点数之和/部件总节点数≥ε，且关键部件能实现系统大部分功能。

2)通过经验小波变换(ewt)对复杂机电系统关键部件的检测信号进行ewt分解，得到原信号的经验小波函数分量(ewf)。

3)对关键部件进行加速退化实验，记录检测信号的变化。以此得到原信号的经验小波函数分量中各频带幅值随时间变化的函数图像。定义部件性能退化曲线为频带幅值随时间衰减曲线。特征频带幅值衰减比首次达到δi时认定部件失效。

4)根据系统各关键部件的物理模型得到部件之间的耦合关系，确定部件状态变迁的条件和流方向。同时针对系统状态的退化，将系统状态进行离散划分。定义系统故障不可自修复，只能由低故障态向高故障态的转移。综合库所，流关系，与变迁等条件建立系统的petri网模型。

5)定义系统的失效阈值ω，当系统达到失效阈值时认定系统失效。利用patri网得到系统故障率与部件故障率的相关函数r(r1,r2,...,rs)。

6)根据特征信号确定相应的部件故障率ri(t)，得到变迁后的petri网，确定出系统的故障状态。在系统故障率与部件故障率的相关函数r(r1,r2,...,rs)对应的图像中，得到系统当前故障率到失效阈值的时间差δt，根据系统剩余寿命的定义，时间差δt即为系统的剩余寿命l，实现系统的寿命预测。

本发明达到的有益条件为：本发明通过对系统节点数进行统计建模提取系统关键部件，利用经验小波变换对部件待测信号进行特征提取，然后建立系统的petri模型以实现考虑部件耦合关系的系统级寿命预测。经验小波变化通过建立自适应小波将单一信号分解为不同幅频的分量，实现信号的特征提取。经验小波变换的优势在于其理论基础完备，计算复杂度低，计算量小，对高频特征分量提取效果好，且已在多个领域得到实际应用。而perti网通过变迁的发生导致标志在库所的流动可以模拟系统的动态运行，用变迁表示不同状态之间的变化条件解决了传统系统级寿命预测建立数学模型的难题，确保系统级寿命预测可靠度更高。

附图说明

为了使本发明的目的、技术方案和有益效果更加清楚，本发明提供如下附图进行说明：

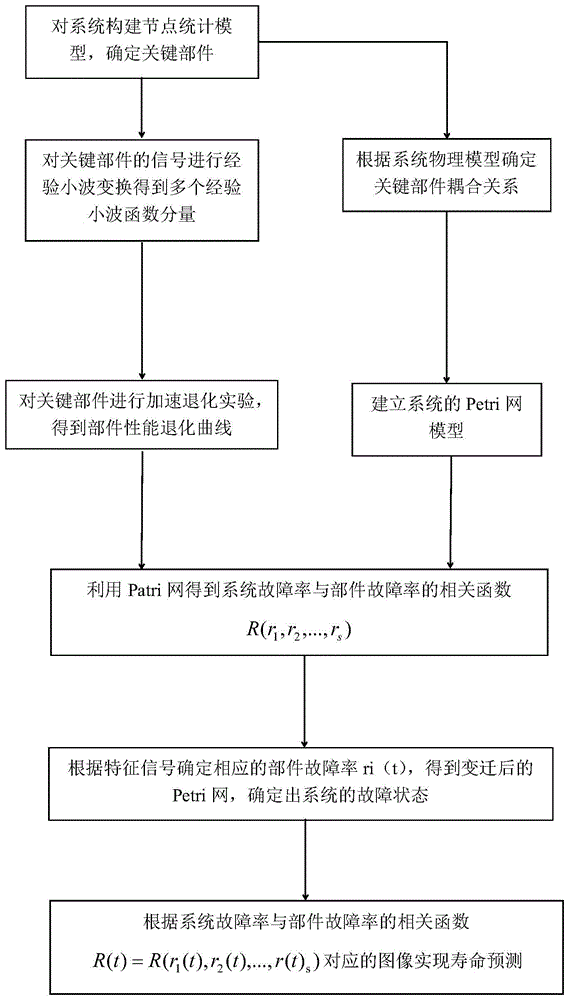
图1为本发明所述复杂机电系统寿命预测方法的流程框图。

图2为本发明所述复杂机电系统寿命预测方法的petri网结构示意图。

具体实施方式

下面将结合附图和具体实施方式，对本发明作进一步的详细阐述。

1)对系统构建部件节点统计模型，分别统计系统共n个部件输入输出节点数并按照降序排列有则部件总结点数如式1所示。

2)确定系统的关键部件，实现系统的降维处理。关键部件定义为：各关键部件节点数之和/部件总节点数≥ε，且关键部件能实现系统大部分功能。对集合中前s个部件的节点数求和得到ks，使得ks/k≥ε。在s个部件的组合能实现系统基本功能的前提下，取s值最小，得到系统的关键部件集合p：

p＝{p1,p2,...,ps}(2)

针对某一复杂机电系统，我们设定其关键部件包括：电气，驱动，控制，传感，机械5个关键部件。

3)对关键部件的待测信号进行傅里叶变换得到频谱f(ω)，对频谱划分出一组频谱分界线。先确定ω边界为[0,π]，在范围内搜索频谱的局部极大值并按照降序排列，归一化处理为0至1。局部极大值个数m＜n时，将频谱分界线个数修正为局部极大值个数,即取n＝m；m≥n时保留前n-1个极大值。取两局部极大值中间频率为频谱分界线，这n-1个分界线将频谱划分为n个部分。

4)根据得到的分界线，利用meyer小波构造方法构造经验尺度函数和经验小波函数，得到正交小波滤波器。meyer小波经验尺度函数和经验小波函数如式(3)和式(4)所示。

其中：

β(x)＝x⁴(35-84x+70x²-20x³)(5)

τn＝γωn(6)

5)用内积的方法确定细节系数和近似系数，细节系数和近似系数分别如式(8)和式(9)所示。

其中，ψn为经验小波函数,上横线表示其复共轭，上角标表示其对应的傅里叶变换。经验模态分量函数可表示为：

6)对关键部件进行加速退化实验，在不改变部件的失效机理和增加新的失效因子的前提下，提高试验应力，如环境应力、热应力等，加速部件的失效进程，促使部件在短期内失效。记录检测信号的变化，以此得到原信号的经验小波函数分量中各频带幅值随时间变化的函数图像。定义部件性能退化曲线为频带幅值随时间衰减曲线，部件故障率为：

ri(t)＝δ(t)×100％(12)

特征频带幅值衰减比δ(t)首次达到δi时认定部件失效。

7)根据系统各关键点的物理模型得到部件之间的耦合关系，确定部件状态变迁的条件和流方向。同时针对系统性能的退化，将系统故障状态进行划分为间歇故障，硬故障，失效。定义系统故障不可自修复，只能由低故障态向高故障态变化。在确定了petri网的库所、变迁和流关系后我们建立出如图2所示的复杂机电系统的petri网模型。在图2所示的petri网中，p1,p2,p3,p4,p5为源库所,p12为目的库所。初始状态m0可表示为如式(13)所示。

m0＝(1,1,1,1,1,0,0,0,0,0,0,0)(13)

m为库所的向量组，“1”表示该库所中含有托肯，“0”表示库所为空。含有托肯的库所即表示为当前状态。通过m的变换来实现用静态的petri网动态显示系统状态的变化。

p1,p2,p3,p4,p5分别表示电气，驱动，控制，传感，机械各部件的正常工作状态，当某部件故障率达到变迁触发条件则引发托肯的转移，即状态的变化，对应部件或是部件构成的子系统故障，表现为库所p6,p7,p8,p9含有托肯。变迁t5的输入输出表现了由部件到系统的转换，库所p10,p11,p12表示系统的三种故障状态：间歇故障，硬故障，失效。变迁t6,t7对应事件定义为系统故障率的变化。

8)定义系统的失效阈值ω，当系统故障率达到失效阈值时认定系统失效。利用patri网得到系统故障率与部件故障率的相关函数：

r(t)＝r(r1(t),r2(t),...,r(t)s)(14)

9)对系统进行寿命预测。以图2所示的一种复杂机电系统petri网模型为例，电气部件与驱动部件构成的子系统耦合，对应petri网模型为多因一果，变迁t1的激发条件定义为{r1(t)≥ρ1|r2(t)≥ρ2}，其中ρ1,ρ2分别为部件的信号衰减比δi对应的失效阈值。同样地，对于变迁t5，可以定义事件f{r1,r2,r3,r4,r5}，当事件f发生时变迁t5使能，状态发生转移，实现由部件到系统的转换。根据各部件当前信号的状态确定相应的部件故障率ri(t)，得到变迁后的petri网，确定出系统的故障状态。剩余寿命定义为：

l＝inf{l＞0:r(l+tk)≥ω|r0:k,r(tk)＜ω}(15)

在系统故障率与部件故障率的相关函数r(t)＝r(r1(t),r2(t),...,r(t)s)对应的图像中，得到当前故障率到失效阈值的时间差δt，根据系统剩余寿命的定义，时间差δt即为系统的剩余寿命l。