一种基于去趋势项的生理电信号熵分析方法与流程

本发明涉及信号处理技术领域，尤其涉及一种基于去趋势项的生理电信号熵分析方法。

背景技术：

最新调查显示，我国每年约有400万人死于各类心血管系统疾病。目前我国包括各种类心血管疾疾病的患者人数已经高达2.9亿，同时由于年轻人工作的不规律和加班量的日益严重，心脏病患者已呈现年轻化的趋势。这些现象均表明，心脏病已成为妨害人类健康的最常见疾病。因而，有效的预防和诊治心血管的功能异常，是当今医学界面临的首要问题，也成为许多学者目前研究的重要课题。目前对心脏系统的输出信号研究主要分为两大类，第一类是分析心电图波形，这种方法简单易操作，并且可以直观的得到分析结果。但是由于心脏系统本身的复杂性，导致心脏系统的随机性非常明显。心电图在获取的过程中也容易受到其他频率信号的干扰。第二类是心率变异性信号，心率变异性信号是从心电图信号中提取的rr间期(相邻两个r波相隔的时间)信号，心率变异性信号是大量离散的数据点，其所蕴含的信息可以反应逐次心跳周期微小差异的变化情况。

由于心电信号非常微弱，在数据采集过程中，不可避免的会遭受人为或外界环境的强干扰，引起采集到的心电波形在正常波动状态时发生畸变。外界因素的干扰可能导致收集的心电信号呈现一定的趋势项。一般方法没有对信号做去趋势，识别效果不佳，在这些不同现象产生的趋势干扰下，不仅降低了实验结果的准确性，甚至可能出现一定程度的误差。目前的心电监测仪器中，都没有对信号做去趋势项处理，直接将测出来的数据进行显示。获得高信号质量的心电信号，这对于特征值参数的提取和进一步分析具有决定性意义，因此首先必须对心电信号进行预处理，从而获得相对保真性强的实验数据对其进行理论分析和研究。对于去除趋势项这一问题，目前尚没有良好的滤波法来消除其内部的频率混叠现象。因此需要提出一种新的技术方案解决上述问题。

技术实现要素：

针对上述问题，本发明提出了一种基于去趋势项的生理电信号熵分析方法，对心率变异性信号基于平滑先验法消除非线性信号趋势，平滑先验法是一种基于正则化原理的去趋势方法，该方法可以根据趋势项的截止频率与特征值参数之间的一对一的数值关系，确定不同频率所对应的趋势项成分，这是小波分析和集合经验模态分解方法所不具有的优势。其次，对标准数据库健康人昼夜节律下的hrv信号叠加不同成分的趋势项，使之呈现一定程度上的单一或混合趋势，然后使用平滑先验法消除hrv信号的趋势项，最后使用近似熵和模糊熵分别计算去趋势前后不同趋势下的熵值。研究结果发现：消除趋势前，在不同趋势的强干扰下，经t检验，p(白天，夜间)＜0.05，即近似熵和模糊熵能够识别出两组不同的样本。然而，当样本被线性、幂律以及三种趋势叠加的混合趋势干扰时，p(白天，夜间)＞0.05，即近似熵和模糊熵均不能识别出存在趋势的两组不同样本，表明近似熵和模糊熵容易受到趋势的影响，使得试验结果不稳定。作为比较，当我们使用平滑先验算法对昼夜节律下的hrv信号进行去趋势项后，不论是hrv信号被单一趋势或是由单一趋势叠加而成的混合趋势强干扰，近似熵和模糊熵值均保持恒定，且经t检验，p(白天，夜间)＜0.05，即经过平滑先验法去趋势后，两种熵分析法可以识别不同趋势干扰下的两组样本，使两种熵具有了处理信号中存在趋势或噪声的优势。

本发明通过以下技术方案来实现上述目的：

一种基于去趋势项的生理电信号熵分析方法，包括以下步骤：

步骤1，选取合适的信号序列；本专利的所有数据来自physionet，该网站是由美国国立卫生研究院和波士顿大学以及波士顿医学中心共同建立的为全世界各地的医学信号研究者提供便捷。

步骤2，对信号序列进行预处理：在提取出的rr间期信号存在异位起搏点和伪差等成分，在进行实验之前，对数据进行预处理，将满足以下不等式的信号保留，去除其它不满足的点；

500＜rri＜1500；

其中rri是rr间期序列，是rr间期序列的平均值；

步骤3，对预处理后的心率变异性信号计算其近似熵值和模糊熵值，并对结果进行独立性t检验，结果显示两组信号的近似熵值曲线和模糊熵值曲线可以被完全区分开，可以将两组样本完全区分开；

步骤4，向原始信号中增加线性、幂律、周期性趋势以及三种趋势叠加的混合趋势，其中线性趋势参数为(al＝0.001)、周期性趋势参数为(as＝0.2，t＝500)以及幂律性趋势的参数为(ap＝2，j＝0.2)；

步骤5，对加入趋势项的心率变异性信号计算其近似熵值和模糊熵值，并对结果进行独立性t检验，结果显示两组信号的近似熵值曲线和模糊熵值曲线不能被区分开，因此在实际的实验中对才到的心率变异性信号需要进行去趋势处理后才能进行熵分析；

步骤6，对具有趋势项的信号使用平滑先验法，去除待处理信号中的趋势项，保留有效的信号成分；

步骤7，对去趋势后的心率变异性信号计算其近似熵值和模糊熵值，并对结果进行独立性t检验，结果显示两组信号的近似熵值曲线和模糊熵值曲线可以被完全区分开，可以将两组样本完全区分开。

进一步方案为，所述步骤3中：对预处理后的心率变异性信号计算近似熵值，具体步骤如下：

1)首先给定嵌入维数m和相似容限r，对于获取的原始时间序列u(i)，共n个数据点，按顺序形成m维矢量x(i)，即：

x(i)＝[u(i)，u(i+1)，…u(i+m-1)]，i＝1，2，…，n-m+1；

2)对于每一个i值，计算x(i)与其余矢量x(j)之间的距离，并以d[x(i)，x(j)]表示x(i)、x(j)中差值最大的一个，即：

3)根据预定的相似容限r(r＞0)，对每个i值统计：d[x(i)，x(j)]＜r的数目，并记此数目与总的矢量个数n-m+1的比值为即：

4)求的对数，再将其所有i求平均值记为c^m(r)，即：

5)将维数加1，形成m+1维，重复以上步骤，得到c^m+1(r)和

6)此序列的近似熵为：

但是在现实情况中，处理的数据长度都是有限长序列，则当序列有限长时：

apen(m，r)＝c^m(r)-cm⁺¹(r)：

其中采用标准近似熵(2，r，n)分析昼夜节律下的hrv时间序列，其中嵌入维数m＝2，r为相似容限(通常取0.1～0.5sd，本文取r＝0.2sd)(sd代表信号的标准差)。

进一步方案为，所述步骤3中：对预处理后的心率变异性信号计算模糊熵值，具体步骤如下：

1)对于一个m点采样序列定义：{u(j)：1≤j≤m}；

2)按照序号的连续顺序重构生成的一组n维矢量，

其中{u(j)，u(j+1)，…，u(j+n-1)}，代表第j个点开始连续n个u的值，u0(j)表示均值见式子；

3)定义两个n维矢量和之间的距离为两者对应元素中差值最大的一个，即：

4)用模糊函数定义两个矢量和的相似度即：

上式中函数为指数函数，m，r分别是指数函数边界的梯度和宽度；

5)定义函数

6)重复2～5步骤，按照序号顺序重构一组n+1维矢量，函数定义如下：

7)模糊熵定义为

当m值为有限值时，综上所有步骤，可得到序列长度为m的模糊熵的估计值fuzzyen(n，m，r，m)＝lno^m(m，r)-lno^m+1(m，r)；

其中试验参数设置为：m＝2，r＝0.2sd，sd为数据的标准差。

进一步方案为，所述步骤6中：基于平滑先验法对加入趋势项的信号进行去趋势项处理，具体步骤如下：

该算法假设原始数据信号，即时间序列z由两部分组成：

z＝zs+zt；

在上面公式zs是平稳项；zt是非线性的低频趋势成分，也可用下面公式表示：

zt＝hθ+v；

其中，h∈r^n×m代表观测矩阵，θ∈r^m代表回归参数，v表示观测误差，实验目标就转化为使用优化方法用以估计参数θ，使来估计原信号中的趋势项；估计参数θ的常用方法是最小二乘法，而平滑先验法是在寻优过程中添加了微分项||dd(hθ)||，使其将至最低，以确保hθ能够消除掉信号中的趋势项部分：

式中：λ为正则化参数，dd为离散化d阶微分算子矩阵。矩阵dd的求解方式如下：

设时间序列z中包含n个局部极值点，用列项量r＝[r1，r2，…rn]^t∈rⁿ表示，r的一阶趋势为：r1＝[r2-r1，…，rn-rn-1]，二阶趋势为：

r2＝[r3-r2-(r2-r1)，r4-r3-(r3-r2)，…，rn-rn-1-(rn-1-rn-2)]^t；

以此递推，可获得r的任意阶趋势的离散形式，即r的d阶微分可用dd表示为：

解得：和其中就是需要消除的趋势项的估计值；

矩阵h可以通过分析原始信号z的特性获取，为了简便分析，h采用单位矩阵i∈r^n×n表示；对于矩阵dd，当阶数为2时，不会影响原始信号的周期性趋势(hrv信号通常以周期趋势呈现较多)，且可以很好的分析信号中的非周期性趋势项(即非线性趋势)，因此dd的阶数取2，d2∈r^(n-2)×n可表示为：

因此，原始信号消除趋势项后的平稳部分表示为：

本发明的有益效果在于：

本发明提出了一种基于去趋势项的生理电信号熵分析方法，该方法可以根据趋势项的截止频率与特征值参数之间的一对一的数值关系，确定不同频率所对应的趋势项成分，这是小波分析和集合经验模态分解方法所不具有的优势。其次，对标准数据库健康人昼夜节律下的hrv信号叠加不同成分的趋势项，使之呈现一定程度上的单一或混合趋势，然后使用平滑先验法消除hrv信号的趋势项，最后使用近似熵和模糊熵分别计算去趋势前后不同趋势下的熵值。两种熵分析法可以识别不同趋势干扰下的两组样本，使两种熵具有了处理信号中存在趋势或噪声的优势，为非线性信号处理以及特征值选择开辟了另一个重要的途径。

附图说明

为了更清楚地说明本发明实施例中的技术方案，下面将对实施例或现有技术描述中所需要实用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本实施例的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

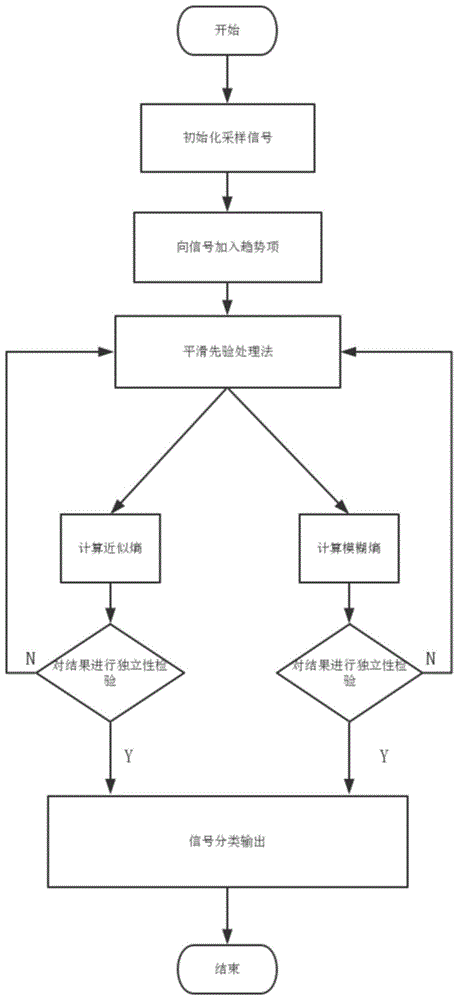
图1是本发明的基于去趋势项的生理电信号熵分析流程图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面将对本发明的技术方案进行详细的描述。显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所得到的所有其它实施方式，都属于本发明所保护的范围。

在任一实施例中，如图1所示，本发明的一种基于去趋势项的生理电信号熵分析方法，包括以下步骤：

步骤1，选取合适的信号序列；

步骤2，对信号序列进行预处理：在提取出的rr间期信号存在异位起搏点和伪差等成分，在进行实验之前，对数据进行预处理，将满足以下不等式的信号保留，去除其它不满足的点；

500＜rri＜1500；

其中rri是rr间期序列，是rr间期序列的平均值；

步骤3，对预处理后的心率变异性信号计算其近似熵值和模糊熵值，并对结果进行独立性t检验，结果显示两组信号的近似熵值曲线和模糊熵值曲线可以被完全区分开，可以将两组样本完全区分开；

所述步骤3中：对预处理后的心率变异性信号计算近似熵值，具体步骤如下：

1)首先给定嵌入维数m和相似容限r，对于获取的原始时间序列u(i)，共n个数据点，按顺序形成m维矢量x(i)，即：

x(i)＝[u(i)，u(i+1)，…u(i+m-1)]，i＝1，2，…，n-m+1；

2)对于每一个i值，计算x(i)与其余矢量x(j)之间的距离，并以d[x(i)，x(j)]表示x(i)、x(j)中差值最大的一个，即：

3)根据预定的相似容限r(r＞0)，对每个i值统计：d[x(i)，x(j)]＜r的数目，并记此数目与总的矢量个数n-m+1的比值为即：

4)求的对数，再将其所有i求平均值记为c^m(r)，即：

5)将维数加1，形成m+1维，重复以上步骤，得到c^m+1(r)和

6)此序列的近似熵为：

但是在现实情况中，处理的数据长度都是有限长序列，则当序列有限长时：

apen(m，r)＝c^m(r)-c^m+1(r)：

其中采用标准近似熵(2，r，n)分析昼夜节律下的hrv时间序列，其中嵌入维数m＝2，r为相似容限(通常取0.1～0.5sd，本文取r＝0.2sd)(sd代表信号的标准差)。

所述步骤3中：对预处理后的心率变异性信号计算模糊熵值，具体步骤如下：

1)对于一个m点采样序列定义：{u(j)：1≤j≤m}；

2)按照序号的连续顺序重构生成的一组n维矢量，

其中{u(j)，u(j+1)，…，u(j+n-1)}，代表第j个点开始连续n个u的值，u0(j)表示均值见式子；

3)定义两个n维矢量和之间的距离为两者对应元素中差值最大的一个，即：

4)用模糊函数定义两个矢量和的相似度即：

上式中函数为指数函数，m，r分别是指数函数边界的梯度和宽度；

5)定义函数

6)重复2～5步骤，按照序号顺序重构一组n+1维矢量，函数定义如下：

7)模糊熵定义为

当m值为有限值时，综上所有步骤，可得到序列长度为m的模糊熵的估计值fuzzyen(n，m，r，m)＝lno^m(m，r)-lno^m+1(m，r)：

其中试验参数设置为：m＝2，r＝0.2sd，sd为数据的标准差。

步骤4，向原始信号中增加线性、幂律、周期性趋势以及三种趋势叠加的混合趋势，其中线性趋势参数为(al＝0.001)、周期性趋势参数为(as＝0.2，t＝500)以及幂律性趋势的参数为(ap＝2，j＝0.2)；

步骤5，对加入趋势项的心率变异性信号计算其近似熵值和模糊熵值，并对结果进行独立性t检验，结果显示两组信号的近似熵值曲线和模糊熵值曲线不能被区分开，因此在实际的实验中对才到的心率变异性信号需要进行去趋势处理后才能进行熵分析；

步骤6，对具有趋势项的信号使用平滑先验法，去除待处理信号中的趋势项，保留有效的信号成分；

所述步骤6中：基于平滑先验法对加入趋势项的信号进行去趋势项处理，具体步骤如下：

该算法假设原始数据信号，即时间序列z由两部分组成：

z＝zs+zt；

在上面公式zs是平稳项；zt是非线性的低频趋势成分，也可用下面公式表示：

zt＝hθ+v；

其中，h∈r^n×m代表观测矩阵，θ∈r^m代表回归参数，v表示观测误差，实验目标就转化为使用优化方法用以估计参数θ，使来估计原信号中的趋势项；估计参数θ的常用方法是最小二乘法，而平滑先验法是在寻优过程中添加了微分项||dd(hθ)||，使其将至最低，以确保hθ能够消除掉信号中的趋势项部分：

式中：λ为正则化参数，dd为离散化d阶微分算子矩阵。矩阵dd的求解方式如下：

设时间序列z中包含n个局部极值点，用列项量r＝[r1，r2，…rn]^t∈rⁿ表示，r的一阶趋势为：r1＝[r2-r1，…，rn-rn-1]，二阶趋势为：

r2＝[r3-r2-(r2-r1)，r4-r3-(r3-r2)，…，rn-rn-1-(rn-1-rn-2)]^t；

以此递推，可获得r的任意阶趋势的离散形式，即r的d阶微分可用dd表示为：

解得：和其中就是需要消除的趋势项的估计值；

矩阵h可以通过分析原始信号z的特性获取，为了简便分析，h采用单位矩阵i∈r^n×n表示；对于矩阵dd，当阶数为2时，不会影响原始信号的周期性趋势(hrv信号通常以周期趋势呈现较多)，且可以很好的分析信号中的非周期性趋势项(即非线性趋势)，因此dd的阶数取2，d2∈r^(n-2)×n可表示为：

因此，原始信号消除趋势项后的平稳部分表示为：

步骤7，对去趋势后的心率变异性信号计算其近似熵值和模糊熵值，并对结果进行独立性t检验，p(白天，夜间)＜0.05，结果显示两组信号的近似熵值曲线和模糊熵值曲线可以被完全区分开，可以将两组样本完全区分开。

这说明平滑先验法消除信号中掺杂的趋势项效果非常明显，并且很大的提高了两种熵分析法的准确度和稳定性。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。在上述具体实施方式中所描述的各个具体技术特征，在不矛盾的情况下，可以通过任何合适的方式进行组合，为了避免不必要的重复，本发明对各种可能的组合方式不再另行说明。本发明的各种不同的实施方式之间也可以进行任意组合，只要其不违背本发明的思想，其同样应当视为本发明所公开的内容。