一种基于GRU神经网络的滚动轴承剩余寿命预测方法与流程

本发明属于滚动轴承剩余寿命预测技术领域，尤其涉及一种基于gru神经网络的滚动轴承剩余寿命预测方法。

背景技术：

在现代工业领域，滚动轴承是旋转机械中最常见、最为关键的机械部件之一。滚动轴承的工作环境具有复杂性和不确定性，因此滚动轴承在机器的使用寿命期间也很容易损坏。一旦轴承因疲劳、磨损、腐蚀等情况而失效，就容易导致机器意外停机情况的发生，甚至导致灾难性损坏，直接影响整个机械设备的运行可靠性。因此，为了提高旋转机械的可靠性和操作安全性，对滚动轴承进行剩余寿命(remainingusefullife，rul)预测显得尤为重要。

目前，最为常用的对滚动轴承进行rul预测的方法是数据驱动方法，比如1)提取特征，利用多尺度卷积神经网络预测轴承的剩余寿命的方法、2)提取特征，利用lstm模型预测轴承的rul的方法、3)提取特征，利用自组织映射模型预测轴承的rul的方法、4)采用小波包经验模态分解方法提取特征，利用ε-svm算法预测轴承的rul的方法。这类方法的建模通常必须经过必要的机器学习和测试步骤，具体为：先收集传感器中采集的原始数据并从中提取特征，再对提取的特征加以选择，保留有效的特征；然后利用回归预测模型来学习机械的退化行为；最后，在测试阶段，通过学习模型预测未来行为和验证模型性能。然而，在上述这类传统的数据驱动方法中提取的特征中存在的波动及噪声，这会影响到预测结果的准确度；而且上述这类方法中采用的这些回归预测模型尚存在对数据不够敏感问题，这也将影响到预测结果的准确度。

技术实现要素：

本发明是为了克服上述存在的问题而进行的，目的在于提供一种能准确预测滚动轴承rul的方法，采用ceemdan算法对提取的传统特征进行分解并提取趋势项作为趋势性特征，以减小传统特征中存在的波动及噪声；同时，利用单调性和相关性准则的线性组合来选择最敏感的特征；然后利用gru神经网络来学习轴承的退化行为，从而实现对滚动轴承rul准确预测。

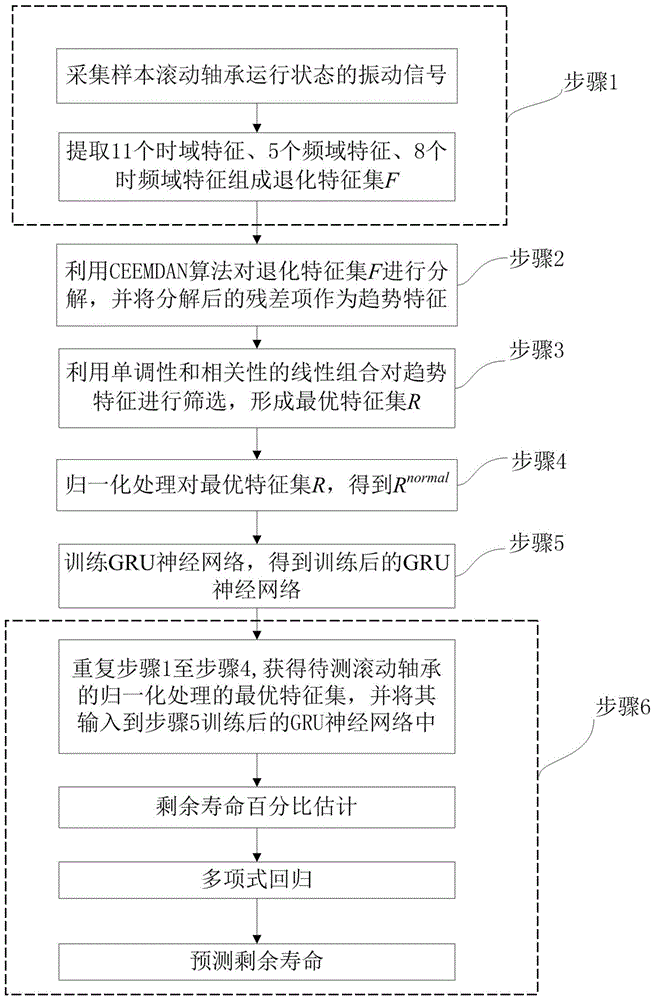
本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法，其特征在于，按照如下步骤进行：步骤1：采集样本滚动轴承运行状态的振动信号，对振动信号提取时域特征、频域特征以及时频域特征，由时域特征、频域特征、时频域特征组成退化特征集；步骤2：利用ceemdan算法对退化特征集进行分解，并将分解后的残差项作为趋势特征；步骤3：利用单调性和相关性的线性组合对趋势特征进行筛选，形成最优特征集；步骤4：对最优特征集进行归一化处理，得到归一化处理后的最优特征集；步骤5：采用gru神经网络，将归一化处理后的最优特征集作为gru神经网络的输入，将剩余寿命百分比作为gru神经网络的输出，以训练gru神经网络；步骤6：重复步骤1～4采集待测滚动轴承的运行状态的振动信号以获取待测滚动轴承的归一化处理的最优特征集，再将待测滚动轴承的归一化处理的最优特征集输入步骤5训练得到的gru神经网络中，从而获得待测滚动轴承的剩余寿命百分比，再利用gru网络输出的待测滚动轴承的剩余寿命百分比预测出待测滚动轴承的rul。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：步骤1中，时域特征为11个，分别是最大绝对值f1、均值f2、均方根值f3、峭度系数f4、偏斜度系数f5、峰-峰值f6、方差值f7、波峰因子f8、波形因子f9、脉冲因子f10、裕度因子f11；频域特征为5个，是将振动信号经过快速傅里叶变换后，取完整的频谱信号f12、四个子部频谱信号f13、f14、f15、f16，再对f12、f13、f14、f15、f16做相似性变换得到的计算结果，表示为f12、f13、f14、f15、f16；时频域特征为8个，是采用haar小波变换对振动信号进行三层小波包分解所得的8个节点能量比，表示为f17、f18、f19、f20、f21、f22、f23、f24；退化特征集表示为f＝{f1,…,fr,…,f24}。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：其中，相似性变换的计算公式如下：

公式(1)中，fq(t)是频谱信号fq(t)相似性变换后的计算结果，fq(t)作为频域特征；fq(t)是频谱信号fq在当前时刻的序列；fq(0)是频谱信号fq在初始时刻的序列；是的均值；是的均值；是频谱信号fq的第m个样本点，其中m是频谱信号fq的总样本数。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：步骤2中，对于退化特征集f中的第r个特征fr，按照如下步骤进行，得到对应的趋势特征rr：步骤2-1：添加一个服从n(0，1)的白噪声得到一个新的信号其计算公式为：

公式(2)中，fr(t)是第r个特征；ε0是原始信号的噪声标准偏差；j是第j次迭代；j是总的迭代次数；步骤2-2：对步骤2-1获得j个新的信号采用经验模态分解(emd)，并获取第1个本征模态函数，其计算公式为：

公式(3)中，是第j个信号emd分解后获得的第1个本征模态函数；是的均值；j是总的迭代次数；步骤2-3：计算出第1个残差项：

公式(4)中，是第1个残差项；fr(t)是第r个特征；是的均值；步骤2-4：判断残差项的极值点个数是否超过2个？当残差项的极值点个数不超过2个，则分解过程结束；当残差项的极值点个数超过2个，则通过如下公式(5)给残差项添加一个服从n(0，1)的白噪声

公式(5)中，是对残差信号添加噪声得到一个新的信号；是第1个残差项；ε1是第1阶段的噪声标准偏差；e1(·)是emd分解后获得的第1个本征模态函数；步骤2-5：根据步骤2-2中对j个新的信号采用经验模态分解(emd)后，获得第1个本征模函数后，可进一步获得第2个本征模函数(k＝2)；对于第k个本征模函数，其计算通式为：

公式(6)中，是第k个本征模函数；是第j个信号emd分解后获得的第个k本征模函数；e1(·)是emd分解后获得的第1个本征模态函数；是第k-1个残差项；εk-1是第k-1阶段的噪声标准偏差；ek-1(·)是emd分解后获得的第k-1个本征模态函数；是一个服从n(0，1)的白噪声；k是总的本征模态函数的个数；步骤2-6：计算第2个残差项(k＝2)；对于第k个残差项的计算公式如下：

公式(7)中，是第k个残差项；是第k-1个残差项；是第k个本征模态函数；步骤2-7：重复步骤2-4至步骤2-6，可得到所有本征模函数以及最后的残差项；将最后的残差项作为第r个特征fr(t)的趋势特征rr(t)，公式表述如下：

公式(8)中，是第k个残差项；fr(t)是第r个特征；是第k个本征模函数；k是总的本征模态函数的个数。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：步骤3具体按照如下步骤进行：步骤3-1：计算各个趋势特征的单调性和相关性，对于第r个趋势特征rr(t)的计算通式为：

公式(9)中，monr是第r个趋势特征的单调性；corrr是第r个趋势特征的相关性；δ(·)是单位阶跃函数；t是寿命期间样本的长度；rr(t)是第r个趋势特征在t时刻的测量值；lr(t)是第r个趋势特征在t时刻的时间值；rr(t+1)是第r个趋势特征在t+1时刻的测量值；lr(t+1)是第r个趋势特征在t+1时刻的时间值；为序列{rr(t)}t＝1:t的平均值；为序列{lr(t)}t＝1:t的平均值；步骤3-2：计算单调性和趋势性的线性组合，选择加权和超出阈值的特征组成最优的特征集。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：步骤3-2中计算单调性mon和趋势性corr的线性组合cri时，对于第r个趋势特征rr(t)的计算通式为：

公式(10)中，ξ1为单调性的权重系数，并设置为0.6；ξ2为相关性的权重系数，并设置为0.4；阈值设置为0.7，选择crir超出设定阈值的特征组成最优的特征集r。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：步骤5中训练gru神经网络包括以下步骤：步骤5-1：将最优特征集序列输入到gru神经网络中，得到隐藏状态的输出步骤5-2：采用整流线性单元作为激活函数，第一层gru网络的输出为：步骤5-3：将输入到dropout层，并且设置每个节点以p＝0.2的随机概率被保留，则得到dropout层的输出为步骤5-4：将输入到第二层gru网络层，按照步骤5-1至步骤5-3得到第二层gru网络层的输出和dropout层的输出步骤5-5：最后将步骤5-4学习得到的特征通过一层回归层输出最后评估的剩余寿命百分比，其中回归层采用sigmoid函数将网络的输出限制在[0,1]之间；步骤5-6：以损失函数loss最小化为优化目标，采用adam优化算法来更新参数：

公式(11)中，yt+τ为t+τ时刻的真实值；是t+τ时刻的估计值；l是样本点的个数；τ是滑动窗口的长度。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：gru神经网络使用重置门用来判断先前隐藏状态哪些信息被丢掉，更新门用来保留当前有用的信息，gru神经网络中重置门rt的计算公式如下：

rt＝σ(wxrxt+whrht-1+br)(12)

公式(12)中，wxr是从输入层到重置门的权重矩阵；whr是循环连接的权重矩阵；xt为当前时刻网络的输入；ht-1是历史隐藏状态；br是偏置值；σ(·)表示sigmoid函数。更新门zt的计算公式如下：

zt＝σ(wxzxt+whzht-1+bz)(13)

公式(13)中，wxz是从输入层到更新门的权重矩阵；whz是循环连接的权重矩阵；bz是偏置值。候选状态ct决定当前输入信息如何与之前的隐藏状态相结合，具体表达式为：

公式(14)中，wxc是从输入层到候选状态的权重矩阵；whc是循环连接的权重矩阵；表示元素相乘操作；rt是重置门的输出。隐藏状态ht使用更新门和候选状态来更新先前的隐藏状态和候选状态，具体表达式为：

公式(15)中，表示元素相乘操作；zt是更新门的输出；ct是候选状态的输出。

进一步地，在本发明提供的基于gru神经网络的滚动轴承剩余寿命预测方法中，还具有这样的特征：步骤6中，利用输出的待测滚动轴承的剩余寿命百分比预测出待测滚动轴承的剩余寿命的具体过程如下：首先，将估计的剩余寿命百分比作为输入，然后训练多项式回归模型，多项式回归模型的表达式为：

hi(t)＝at+b(16)

公式(16)中，a、b是模型的参数；t是当前时刻的时间点；hi(t)是t时刻的剩余寿命百分比。然后，利用训练的回归模型得到预测的剩余寿命百分比hi(t)，直到突破故障阈值；定义hi(tend)＝0轴承失效阈值，对应的时间tend为轴承寿命结束时间；根据预测值和最终阈值，得到轴承的剩余寿命：

公式(17)中，n为估计的剩余寿命百分比长度；tend为轴承寿命结束时间；为估计的剩余寿命值。

本发明的有益效果：

本发明基于gru神经网络的滚动轴承剩余寿命预测方法中，通过对采集的振动信号分别提取时域、频域、时频域特征向量，利用完整集合经验模式分解(ceemdan)算法提取趋势特征，有效地减小传统特征存在的局部波动与噪声；并且基于所提取的趋势特征中存在冗余或无关特征，利用相关性和单调性来选择最优特征集，对最优特征集归一化处理后，输入四层的gru神经网络，输出估计的剩余寿命百分比。进而利用估计的剩余寿命百分比预测待测滚动轴承的rul。通过训练后的gru神经网络得到的剩余寿命百分比，具有较强的趋势性和单调性，能够准确跟踪轴承的退化信息，有效地克服了传统特征不能全面描述轴承退化过程的问题，从而能更加精确地预测轴承的剩余寿命。

附图说明

图1是本发明的基于gru神经网络的滚动轴承剩余寿命预测方法的流程图；

图2是本发明的实施例中样本轴承和待测轴承的单调性和相关性准则线性组合的分布图；

图3是本发明的实施例中样本轴承和待测轴承的单调性和相关性准则线性组合结果的排序图；

图4是对比例m1中待测轴承提取的传统特征(未进行ceemdan分解和特征选择)输入到训练后的gru神经网络得到的剩余寿命百分比示意图；

图5是本发明的实施例中待测轴承的最优特征集输入到训练后的gru神经网络得到的剩余寿命百分比示意图；

图6是本发明的实施例中待测轴承1-3的剩余寿命预测图；

图7是本发明的实施例中待测轴承1-4的剩余寿命预测图。

具体实施方式

为了使本发明实现的技术手段、创作特征、达成目的与功效易于明白了解，以下实施例结合附图对本发明基于gru神经网络的滚动轴承剩余寿命预测方法作具体阐述。

<实施例>

图1是本发明的基于gru神经网络的滚动轴承剩余寿命预测方法的流程图。

如图1所示，一种基于gru神经网络的滚动轴承剩余寿命预测方法，按照如下步骤进行：

(一)特征提取

步骤1：通过在线振动传感器采集样本滚动轴承运行状态的振动信号，然后对振动信号提取时域特征、频域特征以及时频域特征，具体如下：

时域特征为11个，分别是最大绝对值f1、均值f2、均方根值f3、峭度系数f4、偏斜度系数f5、峰-峰值f6、方差值f7、波峰因子f8、波形因子f9、脉冲因子f10、裕度因子f11。

频域特征为5个，是将振动信号经过快速傅里叶变换后，取完整的频谱信号f12(0-12.8khz)、四个子部频谱信号f13(0-3.2khz)、f14(3.2-6.4khz)、f15(6.4-9.6khz)、f16(9.6-12.8khz)，再对f12、f13、f14、f15、f16做相似性变换得到的计算结果，表示为f12、f13、f14、f15、f16。该相似性变换是计算当前时刻信号序列与初始时刻信号序列做相似性度量，采用如下公式进行：

公式(1)中，fq(t)是频谱信号fq(t)相似性变换后的计算结果，fq(t)作为频域特征；fq(t)是频谱信号fq在当前时刻的序列；fq(0)是频谱信号fq在初始时刻的序列；是的均值；是的均值；是频谱信号fq的第m个样本点，其中m是频谱信号fq的总的样本数。

时频域特征为8个，是采用haar小波变换对振动信号进行三层小波包分解所得的8个节点能量比，表示为f17、f18、f19、f20、f21、f22、f23、f24。

由时域特征(f1-f11)、时频域特征(f12-f16)、频域特征(f17-f24)组成退化特征集f＝{f1,…,fr,…,f24}。

步骤2：利用ceemdan算法对退化特征集f中的第r个特征fr,(r＝1,2,…,24)进行分解，并将分解后的残差项rr,(r＝1,2,…,24)作为趋势特征。

对于退化特征集f中的第r个特征fr，按照如下步骤2-1至步骤2-7进行，得到对应的趋势特征rr；

步骤2-1：添加一个服从n(0，1)的白噪声得到一个新的信号其计算公式为：

公式(2)中，fr(t)是第r个特征；ε0是原始信号的噪声标准偏差；j是第j次迭代；j是总的迭代次数。

步骤2-2：对步骤2-1获得j个新的信号采用经验模态分解(emd)，并获取第1个本征模态函数，其计算公式为：

公式(3)中，是第j个信号emd分解后获得的第1个本征模态函数；是的均值；j是总的迭代次数。

步骤2-3：计算出第1个残差项：

公式(4)中，是第1个残差项；fr(t)是第r个特征；是的均值。

步骤2-4：判断残差项的极值点个数是否超过2个？当残差项的极值点个数不超过2个，则分解过程结束；当残差项的极值点个数超过2个，则通过如下公式(5)给残差项添加一个服从n(0，1)的白噪声

公式(5)中，是对残差信号添加噪声得到一个新的信号；是第1个残差项；ε1是第1阶段的噪声标准偏差；e1(·)是emd分解后获得的第1个本征模态函数。

步骤2-5：根据步骤2-2中对j个新的信号采用经验模态分解(emd)后，获得第1个本征模函数后，可进一步获得第2个本征模函数(k＝2)。对于第k个本征模函数，其计算公式为：

公式(6)中，是k个本征模函数；是第j个信号emd分解后获得的第个k本征模函数；ek(·)是emd分解后获得的第k个本征模态函数；是第k-1个残差项；εk-1是第k-1阶段的噪声标准偏差；ek-1(·)是emd分解后获得的第k-1个本征模态函数；是一个服从n(0，1)的白噪声；k是总的本征模态函数的个数。

步骤2-6：计算第2个残差项(k＝2)。对于第k个残差项的计算公式如下：

公式(7)中，是第k个残差项；是第k-1个残差项；是第k个本征模态函数。

步骤2-7：重复步骤2-4至步骤2-6，可得到所有本征模函数以及最后的残差项。将最后的残差项作为第r个特征fr(t)的趋势特征rr(t)，公式表述如下：

公式(8)中，是第k个残差项；fr(t)是第r个特征；是第k个本征模函数；k是总的本征模态函数的个数。

(二)特征筛选

步骤3：利用单调性和相关性的线性组合对步骤2获得的所有趋势特征rr,(r＝1,2,···,24)，按照如下步骤3-1至3-2进行筛选，形成最优特征集r。

步骤3-1：计算各个趋势特征的单调性和相关性，对于第r个趋势特征rr(t)的计算通式为：

公式(9)中，monr是第r个趋势特征的单调性；corrr是第r个趋势特征的相关性；δ(·)是单位阶跃函数；t是寿命期间样本的长度；rr(t)是第r个趋势特征在t时刻的测量值；lr(t)是第r个趋势特征在t时刻的时间值；rr(t+1)是第r个趋势特征在t+1时刻的测量值；lr(t+1)是第r个趋势特征在t+1时刻的时间值；为序列{rr(t)}t＝1:t的平均值；为序列{lr(t)}t＝1:t的平均值。

步骤3-2：计算单调性mon和趋势性corr的线性组合cri时，对于第r个趋势特征rr(t)的计算通式为：

公式(10)中，ξ1为单调性的权重系数，设置为0.6；ξ2为相关性的权重系数，设置为0.4；阈值设置为0.7，选择crir超出设定阈值的特征组成最优的特征集r。

(三)特征归一化处理

步骤4：对最优特征集r进行归一化处理，得到归一化处理后的最优特征集r^normal，对于最优特征集r中第d个特征，计算通式如下：

公式(11)中，rd(t)是最优特征集r中第d个特征在t时刻的样本点；是第d个特征序列的最小值；是第d个特征序列的最大值。

(四)建模

步骤5：采用gru神经网络，将步骤4归一化处理后的最优特征集r^normal作为gru神经网络的输入，将剩余寿命百分比作为gru神经网络的输出，以训练gru神经网络。训练gru神经网络的具体按照步骤5-1至步骤5-8进行：

步骤5-1：在训练过程中，收集样本轴承从开始运行到生命周期结束，共有t个运行周期，设置滑动窗口的长度为τ，则输入样本为：

xt+τ＝[r^normal(t),r^normal(t+1),…,r^normal(t+τ-1)](12)

公式(12)中，d是选择的最优特征集的维度；r^normal(t)是归一化处理后的最优特征集；对应的标签值为剩余寿命百分比，具体的表达式为：

公式(13)中，yt+τ是网络对应的标签值；t是轴承寿命期间样本的长度；τ是滑动窗口的长度，设置为τ＝100。输入到网络中的样本个数为：

l＝t-τ(14)

公式(14)中，t是轴承寿命期间样本的长度；τ是滑动窗口的长度。

步骤5-2：归一化处理后的最优特征集输入到gru神经网络中，每个输入序列单元xt获得对应的gru神经网络隐藏状态的输出

步骤5-3：采用整流线性单元作为激活函数，第一层gru网络的输出为：

步骤5-4：将输入到dropout层，并且设置每个节点以p＝0.2的随机概率被保留，则得到dropout层的输出为

步骤5-5：将输入到第二层gru网络层，按照步骤5-2至步骤5-4得到第二层gru网络层的输出和dropout层的输出

步骤5-6：最后将步骤5-5学习得到的特征，通过一层回归层输出最后评估的剩余寿命百分比其中回归层采用sigmoid函数将网络的输出限制在[0,1]之间。

步骤5-7：以损失函数loss最小化为优化目标，采用adam优化算法来更新参数：

公式(15)中，yt+τ为t+τ时刻的真实值；是t+τ时刻的估计值；l是样本点的个数；τ是滑动窗口的长度。

步骤5-8：gru神经网络中使用重置门用来判断先前隐藏状态哪些信息被丢掉，更新门用来保留当前有用的信息，具体步骤如下：

其中重置门rt的计算公式如下：

rt＝σ(wxrxt+whrht-1+br)(16)

公式(16)中，wxr是从输入层到重置门的权重矩阵；whr是循环连接的权重矩阵；xt为当前时刻网络的输入；ht-1是历史隐藏状态；br是偏置值；σ(·)表示sigmoid函数。

更新门zt的计算公式如下：

zt＝σ(wxzxt+whzht-1+bz)(17)

公式(17)中，wxz是从输入层到更新门的权重矩阵；whz是循环连接的权重矩阵；bz是偏置值。

候选状态ct决定当前输入信息如何与之前的隐藏状态相结合，具体表达式为：

公式(18)中，wxc是从输入层到候选状态的权重矩阵；whc是循环连接的权重矩阵；表示元素相乘操作；rt是重置门的输出。

隐藏状态ht使用更新门和候选状态来更新先前的隐藏状态和候选隐藏状态，具体表达式为：

公式(19)中，表示元素相乘操作；zt是更新门的输出；ct是候选状态的输出。

(五)预测剩余寿命

步骤6：重复步骤1～4采集待测滚动轴承的运行状态的振动信号以获取待测滚动轴承的最优特征集，然后，将待测滚动轴承的最优特征集输入步骤5训练得到的gru神经网络中，通过输出的待测滚动轴承的剩余寿命百分比预测出待测滚动轴承的剩余寿命。

其中，利用gru神经网络输出的剩余寿命百分比预测轴承的剩余寿命的具体过程如下：

步骤6-1：将gru神经网络输出的剩余寿命百分比作为多项式回归模型的输入，以训练多项式回归模型，该模型的表达式为：

hi(t)＝at+b(20)

公式(20)中，a、b是模型的参数；t是当前时刻的时间点；hi(t)是t时刻的剩余寿命百分比。

步骤6-2：利用训练的回归模型得到预测的剩余寿命百分比hi(t)，直到突破故障阈值。定义hi(tend)为轴承失效阈值，对应的时间为轴承寿命结束时间。根据预测值和最终阈值，可以得到轴承的剩余寿命。

公式(21)中，n为估计的剩余寿命百分比长度；tend为轴承寿命结束时间；为估计的剩余寿命值。

<实施例的实验结果>

按照上述步骤进行了具体试验：轴承1-1、轴承1-2为样本轴承，通过采集其运行状态的振动信号进行如上述步骤1至步骤5，以训练gru神经网络，得到训练后的gru神经网络；轴承1-3、轴承1-4、轴承1-5、轴承1-6、轴承1-7为待测轴承，本实施例中用待测轴承验证来验证本发明的基于gru神经网络的滚动轴承剩余寿命预测方法的测试效果。

图2描述了样本轴承与待测轴承提取的特征的cri分布情况。图3描述了样本轴承与待测轴承提取的特征对应的cri均值排列情况。

在本实施例的试验过程中，步骤3-2的设定阈值如图3的虚线所示，设定该阈值＝0.7，按照步骤3-2，选择图3的24个趋势特征r1-r24中crir超出设定阈值的特征组成最优的特征集r，即选择时域特征(r4)、频域特征(r12、r15)、时频域特征(r17、r18、r19、r20、r21、r22、r23、r24)，组成的优特征集r＝{r4、r12、r15、r17、r18、r19、r20、r21、r22、r23、r24}，对应在步骤4的公式(11)中d的取值相应为d＝{4,12,15,17,18,19,20,21,22,23,24}。

图5是本发明的实施例中待测轴承(轴承1-3、轴承1-4、轴承1-5、轴承1-6、轴承1-7)的最优特征集输入到训练后的gru神经网络得到的剩余寿命百分比示意图。

图6是本发明的实施例中待测轴承1-3的剩余寿命预测图；图7是本发明的实施例中待测轴承1-4的剩余寿命预测图。

为评价本发明的基于gru神经网络的滚动轴承剩余寿命预测方法的预测效果，将待测轴承预测的剩余寿命与真实的剩余寿命rul通过如下三个评价指标score、mae、nrmse进行计算：

①评分函数(score)：

公式(22)中，ruli是第i个待测轴承的剩余寿命的真实值；是第i个待测轴承的剩余寿命的预测值；i是待测轴承的个数。

对于本实施例，待测轴承为5个(轴承1-3、轴承1-4、轴承1-5、轴承1-6、轴承1-7)，预测剩余寿命分别是：5760s、3300s、1630s、1990s、8430s；真实剩余寿命rul分别是：5730s、2900s、1610s、1460s、7570s。因此上述公式(22)得出的结果为score＝0.4266。

②平均绝对误差(mae)：

公式(23)中，ruli是第i个待测轴承的剩余寿命的真实值；是第i个待测轴承的剩余寿命的预测值；i是待测轴承的个数。

对于本实施例的5个待测轴承，上述公式(23)得出的结果为mae＝368.0。

③归一化均方根误差(nrmse)：

公式(24)中，ruli是第i个待测轴承的剩余寿命的真实值；是第i个待测轴承的剩余寿命的预测值；i是待测轴承的个数。

对于本实施例的5个待测轴承，上述公式(24)得出的结果为nrmse＝0.1151。

score系数值在[0,1]之间，值越接近1，预测的性能越好。nrmse和mae两个指标越接近0，剩余寿命预测的准确性越高。

<对比例>

为验证本发明的基于gru神经网络的滚动轴承剩余寿命预测方法相较于传统的滚动轴承剩余寿命预测方法(m1-m5)的优越性，结合以下对比例实施情况与实施例的实施情况进行分析。采用pronostia平台获得数据集，pronostia平台是一个加速测试平台，描述了轴承在整个使用寿命内的自然退化过程。加速度计每10s采样一次，采样频率为25.6khz，采样持续时间为0.1s。两个加速器垂直安装在轴承上，收集水平和垂直方向的振动信号。本发明基于gru神经网络的滚动轴承剩余寿命预测方法仅采用水平信号，并且本发明使用同种工况下的数据集，其中轴承1-1、轴承1-2作为样本轴承，轴承1-3、轴承1-4、轴承1-5、轴承1-6、轴承1-7作为待测轴承来验证本发明方法的有效性。

对比例m1：提取了轴承的本发明中的时域、频域、时频域特征，但未进行ceemdan分解和特征选择处理，然后将这些特征输入到gru神经网络中估计轴承的剩余寿命。

对比例m2：提取了轴承的本发明中的时域、频域、时频域特征，然后将这些特征输入到多尺度卷积神经网络中估计轴承的剩余寿命。

对比例m3：提出了一些新的其他特征，并用lstm来构建基于剩余寿命百分比与特征之间的映射关系。

对比例m4：提出了一种基于小波包经验模态分解的特征提取方法，基于这些特性，采用自组织映射模型预测剩余寿命对剩余寿命进行了评估。

对比例m5：基于ε-svm估计滚动轴承的剩余寿命。

<实施例与对比例的实验数据及结果分析>

图4是对比例m1中待测轴承提取的传统特征(提取了本发明中的时域、频域、时频域特征，但未进行ceemdan分解和特征选择处)输入到训练后的gru神经网络得到的剩余寿命百分比示意图；图5是本发明的实施例中待测轴承的最优特征集输入到训练后的gru神经网络得到的剩余寿命百分比示意图。

由图4、图5比较可以看出，本发明的基于gru神经网络的滚动轴承剩余寿命预测方法估计的剩余寿命百分比随运行时间变化趋势明显，能够准确地跟踪轴承的退化过程，而m1方法得出的剩余寿命百分比具有明显的波动。且本发明中五个测试集估计的剩余寿命百分比的cri均值为0.982，高于m1估计的剩余寿命百分比的cri均值和所选择的所有单特征。上述结果表明，本发明的基于gru神经网络的滚动轴承剩余寿命预测方法能更有效地跟踪轴承的退化过程。

表1记载了本发明实施例与对比例(各种传统方法)的预测剩余寿命的实验结果。

从表1数据可知，本发明的基于gru神经网络的滚动轴承剩余寿命预测方法在上述这些方法中得分(评分函数score值)最高，平均绝对误差(mae)最小，归一化均方根误差(nrmse)最小。由于score系数值越接近1，表示预测的性能越好，nrmse和mae两个指标越接近0，表示剩余寿命预测的准确性越高，因此，表1中实验结果表明：本发明的基于gru神经网络的滚动轴承剩余寿命预测方法相较于传统的这些方法，能够提高退化过程跟踪能力和预测的精度。

上述实施方式为本发明的优选案例，并不用来限制本发明的保护范围。对于本领域的技术人员而言，凡在本发明的精神和原则之内所做的任何修改、替换和变形，均应包含在本发明的保护范围之内。