一种基于Lorenz系统的风速区间预测方法及系统与流程
本发明涉及风速预测领域,特别是涉及一种基于lorenz系统的风速区间预测方法及系统。
背景技术:
近年来,全球能源形势日趋严峻,能源需求不断增大。作为一种清洁可再生能源,风能在世界各地的新能源应用方面备受关注,风力发电并网技术已成为国际研究的热点。国际能源署(iea)报告称,预计2019年风力发电量将增加3.25亿千瓦。然而,风的波动往往会导致风电一体化后电力系统的不稳定。因此,有效的风速预测可以促进风电行业的智能化发展,准确的风速预测是风电大规模开发利用的重要前提。
技术实现要素:
本发明的目的是提供一种基于lorenz系统的风速区间预测方法及系统,用以获得高精度预测结果的同时提高预测模型的可靠性。
为实现上述目的,本发明提供了如下方案:
一种基于lorenz系统的风速区间预测方法,所述方法包括:
获取原始风速序列;对所述风速序列进行变分模态分解(vmd),获取去噪序列和噪声余项;
建立长短时神经网络预测模型(lstm),对所述去噪序列进行初步预测,获取初步预测结果;
通过定义风速爬坡事件(wsr)和风速爬坡率,对初步预测结果进行修正,获取修正的风速预测结果;
通过lorenz方程描述大气动力系统对风速的影响,并得到lorenz扰动序列(lds);
通过b样条插值法对lds进行拟合,并对拟合结果固定置信区间,获取风速扰动区间的上限和下限;
将修正的风速预测结果和风速扰动区间进行求和,获取风速的区间预测结果。
可选的,所述获取去噪序列和噪声余项,具体包括:
获取原始风速数据;
设定分解个数;在确定的分解个数下通过迭代计算包含所有模态的集合和他们的中心频率;获取风速信号的本征模态函数分量和噪声余项;
将风速信号的本征模态函数分量进行重构,获取去噪的风速序列。
可选的,所述建立长短时神经网络预测模型,对所述去噪序列进行初步预测,获取初步预测结果,具体过程包括:
将去噪的风速序列根据9∶1的比例划分为训练集和测试集;
设定长短时神经网络的网络结构,包括输入层神经元个数,隐含层神经元个数和输出层神经元个数;
通过将训练集输入长短时神经网络进行训练;
将测试集输入训练好的长短时神经网络,获取风速的初步预测结果。
可选的,对所述定义风速爬坡事件和风速爬坡率,对初步预测结果进行修正,获取修正的风速预测结果,具体包括:
计算风速梯度;根据风速梯度引入风速爬坡的定义;
当梯度的绝对值大于阈值1,且当前时刻的正梯度增大超过正梯度阈值2或负梯度减小超过负梯度阈值3时,用当前时刻的误差修正下一时刻的风速预测值;
对于阈值1,阈值2和阈值3,将其转化为一个多目标优化问题,以最小化均方根误差为目标,用粒子群算法(pso)求解该优化问题。
可选的,所述通过lorenz方程描述大气动力系统对风速的影响,并得到lds,具体包括:
给定初始条件(0,1,1),求解lorenz方程,获取三维lds;
根据切比雪夫距离,将三维的lds转化为一维的扰动序列。
可选的,所述通过b样条插值法对lds进行拟合,并对拟合结果固定置信区间,获取风速扰动区间的上限和下限,具体包括:
通过b样条差值对lds的分布进行拟合,获取b样条差值拟合函数;
分别固定置信区间为90%和98%,计算拟合函数的上下分位数点;
将上分位点设定为区间预测的上限,将下分位点设定为区间预测的下限。
可选的,所述将修正的风速预测结果和风速扰动区间进行求和,获取风速的区间预测结果,具体包括:
通过将90%置信区间下的上下分位点加减到修正的风速预测结果上,得到90%置信区间下的风速区间预测结果;
通过将98%置信区间下的上下分位点加减到修正的风速预测结果上,得到98%置信区间下的风速区间预测结果。
本发明还提供了一种基于lorenz系统的风速区间预测系统,所述预测系统包括:
风速数据获取和去噪模块,用于获取原始风速序列;对所述风速序列进行变分模态分解,获取去噪序列和噪声余项;
风速数据初步预测模块,用于建立长短时神经网络预测模型,对所述去噪序列进行初步预测,获取初步预测结果;
基于风速爬坡的初步预测结果修正模块,用于通过定义风速爬坡事件和风速爬坡率,对初步预测结果进行修正,获取修正的风速预测结果;
获取lds模块,用于通过lorenz方程描述大气动力系统对风速的影响,并得到lds;
获取扰动上下限模块,用于通过b样条插值法对lds进行拟合,并对拟合结果固定置信区间,获取风速扰动区间的上限和下限;
预测模块,用于将修正的风速预测结果和风速扰动区间进行求和,获取风速的区间预测结果。
可选的,所述风速数据获取和去噪模块具体包括:
获取本征模态分量单元,用于获取原始风速数据;设定分解个数;在确定的分解个数下通过迭代计算包含所有模态的集合和他们的中心频率;获取风速信号的本征模态函数分量和噪声余项;
获取去噪风速序列单元,用于将风速信号的本征模态函数分量进行重构,获取去噪的风速序列。
可选的,所述风速数据初步预测模块,具体包括:
划分划分分风速序列单元,用于将去噪的风速序列根据9∶1的比例划分为训练集和测试集;
设定长短时神经网络的网络结构单元,用于包括输入层神经元个数,隐含层神经元个数和输出层神经元个数;
训练模型单元,用于通过将训练集输入长短时神经网络进行训练;
预测单元,用于将测试集输入训练好的长短时神经网络,获取风速的初步预测结果。
可选的,所述基于风速爬坡的初步预测结果修正模块,具体包括:
定义风速爬坡单元,用于计算风速梯度;根据风速梯度引入风速爬坡的定义;
定义修正方法单元,用于当梯度的绝对值大于阈值a,且当前时刻的正梯度增大超过正梯度阈值b或负梯度减小超过负梯度阈值c时,用当前时刻的误差修正下一时刻的风速预测值;
求解阈值单元,用于对于阈值a,b和c,将其转化为一个多目标优化问题,以最小化均方根误差为目标,用pso求解该优化问题。
可选的,所述获取lds模块具体包括:
获取三维lds单元,用于给定初始条件(0,1,1),求解lorenz方程,获取三维lds;
获取一维lds单元,用于根据切比雪夫距离,将三维的lds转化为一维的lds。
可选的,所述获取扰动上下限模块具体包括:
拟合单元,用于通过b样条差值对lds的分布进行拟合,获取b样条差值拟合函数;
分位点计算单元,用于分别固定置信区间为90%和98%,计算拟合函数的上下分位数点;
确定区间预测上下限单元,用于将上分位点设定为区间预测的上限,将下分位点设定为区间预测的下限。
可选的,所述预测模块具体包括:
90%置信区间下区间预测结果单元,用于通过将90%置信区间下的上下分位点加减到修正的风速预测结果上,得到90%置信区间下的风速区间预测结果;
98%置信区间下区间预测结果单元,用于通过将98%置信区间下的上下分位点加减到修正的风速预测结果上,得到98%置信区间下的风速区间预测结果。
与现有技术相比,本发明具有以下技术效果:
本发明的风速预测方法及系统为基于lorenz系统的风速区间预测过程。首先,采用信号分解技术vmd来进行降噪过程,其次,用长短时神经网络对降噪处理后的数据进行预测,然后,引入风速梯度,对初步预测结果进行修正,得到修正的风速预测结果,在此基础上,再引入洛伦兹扰动理论描述大气动力系统,求解lorenz方程得到lds,采用b样条插值拟合lds的分布,通过固定拟合函数的不同置信区间,得到区间预测的上限和下限。本发明考虑大气动力系统对风速的影响作用,提出的风速区间预测方法有效提高了短期风速预测模型的精度和预测结果的可靠性。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动性的前提下,还可以根据这些附图获得其他的附图。
图1为本发明实施例1基于lorenz系统的风速区间预测方法的流程图;
图2为本发明实施例2提供的预测方法的流程图;
图3为本发明实施例3提供的预测系统的结构框图;
图4为本发明在数据集1上的6个单一模型的预测结果示意图;
图5为本发明在数据集2上的6个单一模型的预测结果示意图;
图6为本发明在数据集1上的修正后预测结果示意图;
图7为本发明在数据集2上的修正后预测结果示意图;
图8为本发明在数据集1上当置信区间为90%时的区间预测结果示意图;
图9为本发明在数据集1上当置信区间为98%时的区间预测结果示意图;
图10为本发明在数据集2上当置信区间为90%时的区间预测结果示意图;
图11为本发明在数据集2上当置信区间为98%时的区间预测结果示意图。
具体实施方式
下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
为使本发明的上述目的、特征和优点能够更加明显易懂,下面结合附图和具体实施方式对本发明作进一步详细的说明。
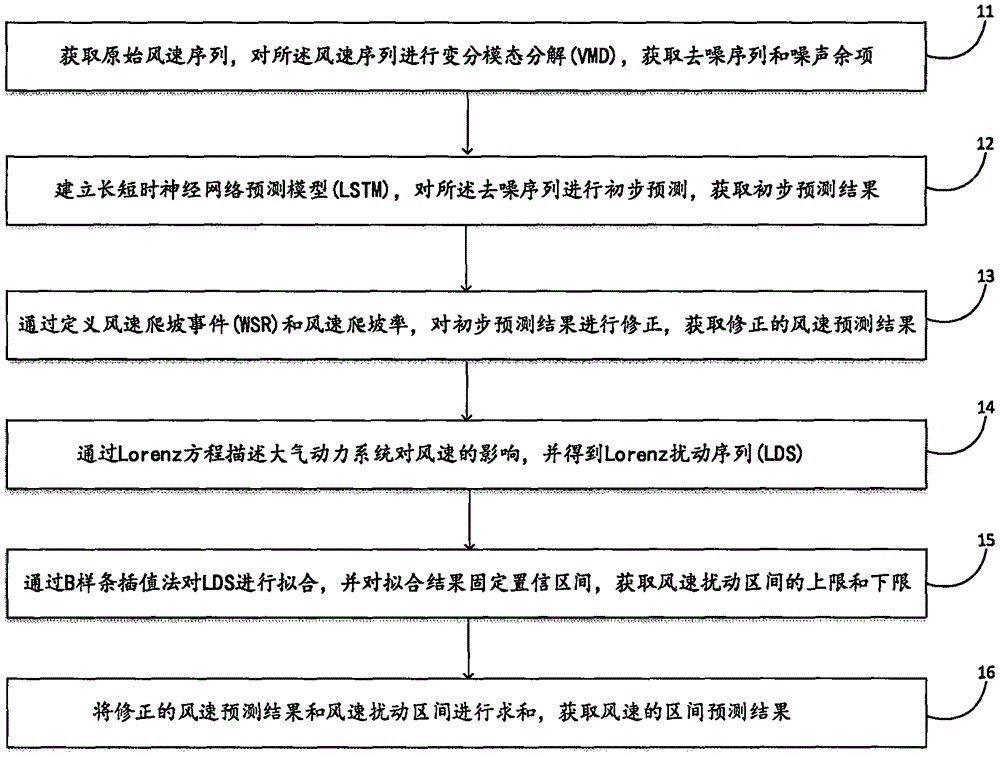
图1为本发明风速区间预测方法的流程示意图。如图1所示,基于lorenz系统的风速区间预测方法包括以下步骤:
步骤11:获取原始风速序列,对所述风速序列进行变分模态分解,获取去噪序列和噪声余项。
目前,vmd可以滤除具有频率特性的序列,留下一个杂乱的噪声部分。在本发明中,利用信号处理方法变分模态分解法对风速进行分解再重构,进行去噪,得到去噪序列和噪声余项。具体步骤如下:
步骤111:所述去噪序列构造当前模态数下的约束变分模型:首先,对于每一个模态分量
式中,
步骤112:引入二次惩罚因子α和lagrange乘法算子λ(t),将约束性问题变为非约束性问题,扩展的lagrange表达式如下:
步骤113:经过傅里叶等距变换等过程得到式(3),实现信号的自适应分解。
其中,
步骤114:迭代更新,直至收敛满足以下条件:
步骤12:建立长短时神经网络预测模型,对所述去噪序列进行初步预测,获取初步预测结果。
随着深度学习技术的不断发展,时间序列的概念被应用在循环神经网络(rnn)的结构设计中。因此,rnn具有良好的时间序列分析能力。而长短时神经网络作为一种改进的rnn,继承rnn对时序数据的分析能力,弥补了rnn在长期记忆方面的不足。由于长短时神经网络模型可以有效地保持较长时间的记忆,在风速预测领域也取得一定成果。
步骤121:将去噪的风速序列按照9∶1分为训练集和测试集,前90%的数据作为训练集,后10%的数据作为测试集;
步骤122:确定长短时神经网络的结构,输入层神经元个数为3,隐含层神经元个数为5,输出层神经元个数为1;
步骤123:将训练集和测试集的数据分别按照公式(6)来构造输入矩阵,
v1,v2,v3...表示第1,2,3...个风速值;
步骤124:将构造好的训练集输入矩阵按行输入到长短时神经网络中,对长短时神经网络进行训练,再将构造好的测试集输入矩阵按行输入到训练好的长短时神经网络中,获取风速初步预测结果。
步骤13:通过定义风速爬坡事件和风速爬坡率,对初步预测结果进行修正,获取修正的风速预测结果,具体包括:
步骤131:根据公式7定义风速爬坡事件,
|v(t0+δt)-v(t0)|/δt>vval(7)
v(t0)为t0时刻的风速值,δt是时间间隔,vval是风速爬坡的阈值;
步骤132:根据公式8定义风速梯度,
k(i)=(v(i)-v(i-1))/imterval(8)
v(i)是第i个风速值,interval是时间间隔;
步骤133:判断第i或i-1个风速值是否大于风速爬坡阈值wrrval,即判断公式9或公式10是否成立,
|k(i-1)|>wrrval(9)
|k(i)|>wrrval(10)
若成立,风速爬坡修正转化为一个多目标优化问题,当正向爬坡增加到一定程度超过正向阈值wrrup,即公式11,
或负向爬坡减小到一定程度超过负向阈值wrrdown,即公式12,
按照公式13对下一时刻的风速预测值进行修正,
步骤134:若公式9和公式10均不成立,不对该时刻的风速预测值进行修正,即修正前后保持不变。
步骤135:对于三个阈值的确定,用粒子群算法(pso);
pso最早是由eberhart和kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。用一种粒子来模拟上述的鸟类个体,每个粒子可视为n维搜索空间中的一个搜索个体,粒子的当前位置即为对应优化问题的一个候选解,粒子的飞行过程即为该个体的搜索过程.粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整.粒子仅具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的方向。每个粒子单独搜寻的最优解叫做个体极值,粒子群中最优的个体极值作为当前全局最优解。不断迭代,更新速度和位置。最终得到满足终止条件的最优解。
步骤1351:初始化,首先设置最大迭代次数为5次,目标函数的自变量个数为3个wrrup,wrrdown,和wrrval,粒子的最大速度为1.5,学习因子为1,位置信息为整个搜索空间,我们在速度区间和搜索空间上随机初始化速度和位置,设置粒子群规模为10,每个粒子随机初始化一个飞翔速度。
步骤1352:求解个体极值与全局最优解,定义目标函数为预测风速与真实风速之间的均方根误差,个体极值为每个粒子找到的最优解(pbest),从这些最优解找到一个全局值(gbest),叫做本次全局最优解。与历史全局最优比较,进行更新。
步骤1353:根据公式14和15更新速度和位置,
vi=vi+c1×rand()×(pbesti-xi)+c2×rand()×(gbesti-xi)(14)
xi=vi+xi(15)
i=1,2,...n,n是粒子的总个数,vi是粒子的速度,rand()是介于(0,1)之间的随机数,xi是粒子当前的位置,c1,c2是学习因子;
步骤1354:终止条件为达到设定迭代次数或代数之间的差值满足最小界限1e10-8;
步骤14:通过lorenz方程描述大气动力系统对风速的影响,并得到lds。
1963年,气象学家爱德华洛伦茨从确定的方程(后来被称为洛伦兹方程)中计算出了非周期现象。洛伦兹系统是数值实验中发现的最早的混沌运动耗散系统。它的状态方程(洛伦兹方程)是天气预报的简化模型。具体步骤如下:
步骤141:建立lorenz方程如公式14,设定参数σ=10,b=8/3,r=28,初始值为(0,1,1),获取三维lds;
步骤142:根据切比雪夫距离公式,将三维的lds进行降维处理,转化为一维的lds;
d(cn-c0)=max(|xn-x0|,|yn-y0|,|zn-z0|)(17)
步骤15:通过b样条插值法对lds进行拟合,并对拟合结果固定置信区间,获取风速扰动区间的上限和下限。
步骤151:对lds绘制频率直方图,设定频率直方图的区间个数为25;
步骤152:用b样条插值法对频率直方图进行拟合,获取拟合函数;
步骤153:设定置信区间,根据拟合函数得到置信上限和置信下限,置信上限取正值,置信下限取负值,获取风速扰动区间的上限和下限;
步骤16:将修正的风速预测结果和风速扰动区间进行求和,获取风速的区间预测结果。
步骤161:将修正的风速预测结果加上扰动区间上限,获取风速区间预测的上限;
步骤162:将修正的风速预测结果减去扰动区间下限,获取风速区间预测的下限
为了验证本发明方法对实际风电场的风速数据具有很好的预测性能,采用西班牙加利西亚的sotavento风电场的风速进行数据仿真实验,图2为本实施例提供的预测方法的流程图。如图2所示,所述具体过程包括:
步骤21:获取原始风速序列
为更好的验证本发明提出方法的预测能力,本实施例选取西班牙加利西亚一座海滨风电场的2个数据集建立了预测模型。数据集1的时间为2018年9月1日00:00至2018年9月7日22:40。第二个数据集的时间为2019年3月9日80:00至2019年3月16日06:30。它们代表了不同季节的风速,时间间隔为10分钟,数据集1中有1000个风速,数据集2中有996个风速。由于数据集2中有四个分散的空缺,我们使用公式(18)所示的线性插值来完成它们。
xt表示第t个时刻,yt表示该时刻对应的风速值,x表示介于xt和xt+i之间的任意时刻,y是其对应的未知的风速值。
对于每个数据集,前900个数据(整个数据的90%)用作训练集,后100个数据用作测试集。也就是说,预测时段是16小时30分钟。
步骤22:定义误差指标
对于确定性预测,本文选取最常用的均方误差(mse)、平均绝对误差(mae)、均方根误差(rmse)和平均绝对百分比误差(mape)进行评价。他们的计算公式如下所示。
yt表示t时刻真实风速,
对于区间预测,应同时考虑区间覆盖率(包含实际风速的区间数之比)和平均区间直径两个方面。因此,定义公式(23)和公式(24)分别描述区间覆盖率和平均区间直径。
nt表示第t个区间是否覆盖了第t个真实风速值,如果nt=1,表示第t个真实风速被覆盖了,如果nt=0,表示第t个真实风速没有被覆盖,rcover表示区间覆盖率,daverage表示平均区间直径。显然,覆盖率越高,平均直径越小,区间预测的效果越好,这说明预测区间较小时预测精度仍然较高。
步骤23:确定性预测结果与讨论
步骤231:首先,比较了自回归滑动平均模型(arma)、支持向量机(svm)、梯度提升决策树(gbdt)、极端梯度提升树(xgboost)、后向传播神经网络(bp)和lstm共6种单风速预测模型的预测结果,并计算了两个数据集上的误差,如表1和表2所示。
步骤232:确定各个模型的参数。根据最小信息准则(aic)确定arma的自相关系数参数p和偏自相关系数参数q。选择最常用的径向基函数作为svm的核心函数。分别通过最小化mae得到gbdt和xgboost的学习率和训练集数,两个模型的提升树数均设置为100。bp的结构为三层,节点数为3-30-1,lstm也设置为三层,节点数为3-5-1。本文在lstm中设置的隐藏层节点数小于bp,因为太多的节点会增加计算时间,尤其是对于lstm(在我们的编程环境中,当使用六个节点时,会消耗一分钟以上的时间),这将大大增加整个模型的计算时间),而且,即使lstm的隐藏层节点较少,其预测性能仍优于bp。
表1数据集1上的单一模型预测误差
表2数据集2上的单一模型预测误差
步骤233:表格计算结果分析。从表1和表2可以看出,lstm神经网络的所有误差指标在任何数据集上都是最小的。从表1可以看出,gbdt的误差最大。与gbdt相比,lstm的mse降低了69.83%,mae降低了46.78%,rmse降低了45.08%,mape降低了53.85%。换句话说,在常用的单一预测模型中,lstm具有最高的预测精度。由表2可知,支持向量机的误差最大。与svm相比,lstm的mse降低了84.63%,mae降低了61.09%,rmse降低了60.79%,mape降低了67.47%。也就是说,与基准预测模型相比,lstm具有最高的预测精度。
步骤234:六个模型在两个数据集上的预测结果分别如图4和图5所示。从图4和图5可以清楚地看出,lstm的预测结果存在明显的一步滞后,因此我们对数据进行去噪,并根据wsr对预测结果进行修改,从而改进了lstm。两个数据集的预测误差分别见表3和表4。
表3在数据集1上的修正后的预测误差对比
表4在数据集1上的修正后的预测误差对比
在表4和表5中,对于不同的分解层数(lev)(两个表中lev为从2到5),我们对wd-lstm实现的最小误差下加了下划线。对于不同的imf个数(表4中的范围为4到8,表5中的范围为3到7),我们将vmd-lstm所达到的最小误差进行了加粗。从这两个表可以看出,当wd分解层数为2时,wd-lstm的误差达到最小。而且,在wsr校正之前,大多数的vmd-lstm误差都小于wd-lstm的最小误差。这充分证明了vmd的去噪效果比wd的去噪效果好得多。在这两个数据集上,通过wsr对预测结果进行修正后,各模型的误差都显著减小。减小比率在5%到30%之间。数据集1上的最小误差由vmd-lstm-psor(imf=6)获得,数据集2上的最小误差由vmd-lstm-psor(imf=4)获得。
步骤235:修正后预测结果分析。图6和图7分别是数据集1当imf=6和数据集2当imf=4的lstm、vmd-lstm和vmd-lstm-psor的预测结果。从这两幅图可以看出,代表lstm预测结果的实线存在明显的一步滞后。经vmd预处理后,风速序列的波动减弱,风速曲线趋于平稳。最后,利用带粒子群优化的wsr对预测结果进行修正,使风场与实际风速曲线较为接近,代表vmd-lstm-psor预测结果的线最接近表示实际风速的线。
步骤24:区间预测结果与讨论
步骤241:分别用kde和b样条插值拟合lds。基于确定性预测结果,根据不同的置信区间,得到了风速的区间预测。覆盖率、平均直径和未覆盖点如表5所示。
表5区间预测结果分析
步骤242:区间预测结果分析。表5分别计算了90%置信区间和98%置信区间下不同拟合方法得到的区间预测结果。对于数据集1,一方面,对于90%置信区间,kde和b样条插值的平均直径几乎相同(分别为1.5009m/s和1.5075m/s),但b样条的覆盖率比kde高2%。b样条区间预测覆盖第2和第74个点,但kde没有。对于98%的置信区间,情况类似。平均直径几乎相同,但b样条的覆盖率比kde高3%。b样条区间预测包括三个点,即点第19、81和95个点,但kde没有。结果表明,当置信区间相同,平均直径基本相同时,kde对lds的拟合效果不如b样条插值的拟合效果好,b样条插值的置信区间可以覆盖更多真实的风速点。另一方面,对于相同的拟合方法,置信区间越大,平均直径越大,这与统计学原理相一致,但不能导致更高的覆盖率。因为更高的置信区间意味着区间预测可能有更高的上限和更高的下限,覆盖范围也会改变(对于kde拟合的lds,90%的置信区间下覆盖了第19、81和85个点而98%的置信区间没有,相反地,98%的置信区间覆盖了点84而90%的置信区间下没有。这种情况与b样条插值拟合lds相似)。这意味着,在不使用高置信区间的情况下,对lds的拟合可以获得更高的覆盖率和更好的区间预测结果。
步骤243:我们在两个数据集上绘制了区间预测的结果,分别如图8,图9,图10,图11所示。图8和图10绘制了90%置信区间下的区间预测结果,图9和图11绘制了98%置信区间下的区间预测结果。区间预测的结果覆盖了大部分实际风速点,表明基于lds的风速区间预测是有效的,用b样条插值拟合lds得到的预测结果优于kde拟合的lds,后者是一种更加有效的方法,和表5所示的一致。
图3为本发明风速预测系统的结构示意图。如图3所示,所述预测系统包括:
风速数据获取和去噪模块31,用于获取原始风速序列;对所述风速序列进行变分模态分解,获取去噪序列和噪声余项。
所述风速数据获取和去噪模块31具体包括:
获取原始风速数据;
设定分解个数;在确定的分解个数下通过迭代计算包含所有模态的集合和他们的中心频率;获取风速信号的本征模态函数分量和噪声余项;
将风速信号的本征模态函数分量进行重构,获取去噪的风速序列。
风速数据初步预测模块32,用于建立长短时神经网络预测模型,对所述去噪序列进行初步预测,获取初步预测结果。
所述风速数据初步预测模块32,具体包括:
将去噪的风速序列根据9∶1的比例划分为训练集和测试集;
设定长短时神经网络的网络结构,包括输入层神经元个数,隐含层神经元个数和输出层神经元个数;
通过将训练集输入长短时神经网络进行训练;
将测试集输入训练好的长短时神经网络,获取风速的初步预测结果。
基于风速爬坡的初步预测结果修正模块33,用于通过定义风速爬坡事件和风速爬坡率,对初步预测结果进行修正,获取修正的风速预测结果;
所述基于风速爬坡的初步预测结果修正模块33,具体包括:
计算风速梯度;根据风速梯度引入风速爬坡的定义;
当梯度的绝对值大于阈值a,且当前时刻的正梯度增大超过正梯度阈值b或负梯度减小超过负梯度阈值c时,用当前时刻的误差修正下一时刻的风速预测值;
对于阈值a,b和c,将其转化为一个多目标优化问题,以最小化均方根误差为目标,用pso求解该优化问题。
获取lds模块34,用于通过lorenz方程描述大气动力系统对风速的影响,并得到lds。
获取lds模块34,具体包括:
给定初始条件(0,1,1),求解lorenz方程,获取三维lds;
根据切比雪夫距离,将三维的lds转化为一维的扰动序列。
获取扰动上下限模块35,用于通过b样条插值法对lds进行拟合,并对拟合结果固定置信区间,获取风速扰动区间的上限和下限。
所述获取扰动上下限模块35,具体包括:
通过b样条差值对lds的分布进行拟合,获取b样条差值拟合函数;
分别固定置信区间为90%和98%,计算拟合函数的上下分位数点;
将上分位点设定为区间预测的上限,将下分位点设定为区间预测的下限。
预测模块36,用于将修正的风速预测结果和风速扰动区间进行求和,获取风速的区间预测结果。
所述预测模块36,具体包括:
通过将90%置信区间下的上下分位点加减到修正的风速预测结果上,得到90%置信区间下的风速区间预测结果;
通过将98%置信区间下的上下分位点加减到修正的风速预测结果上,得到98%置信区间下的风速区间预测结果。
本说明书中各个实施例采用递进的方式描述,每个实施例重点说明的都是与其他实施例的不同之处,各个实施例之间相同相似部分互相参见即可。对于实施例公开的系统而言,由于其与实施例公开的方法相对应,所以描述的比较简单,相关之处参见方法部分说明即可。
本文中应用了具体个例对本发明的原理及实施方式进行了阐述,以上实施例的说明只是用于帮助理解本发明的方法及其核心思想;同时,对于本领域的一般技术人员,依据本发明的思想,在具体实施方式及应用范围上均会有改变之处。综上所述,本说明书内容不应理解为对本发明的限制。
- 还没有人留言评论。精彩留言会获得点赞!