基于蒙特卡洛树搜索的多假设跟踪方法与流程

本发明涉及一种多假设跟踪方法，特别涉及一种基于蒙特卡洛树搜索的多假设跟踪方法。

背景技术：

多假设跟踪(mht)是一类经典的多目标跟踪框架，目前主流的多假设跟踪框架称为tomht(track-orientedmht)，在tomht的工程实现中无法避免的涉及到一类带约束的优化问题-最大团问题，最大团问题是一类经典的组合优化问题，它是一个np完全问题，在很多领域都有应用。在tomht中常常涉及规模很大的最大团问题，目前的主流的tomht项目中采用的解决该优化问题的算法来源于期刊论文“patricr.j.ostergard.anewalgorithmforthemaximum-weightcliqueproblem.nordicjournalofcomputing.volume8issue4,december2001pages424-436”。这是一类运算复杂度较高的精确算法，它能得到最大团的全局最优解，但是由于本问题是np完全问题，在问题规模较大时(邻接矩阵维度达到80-100)时，该算法将难以在可预期的时间内获取精确解，因此在较为复杂的跟踪环境下，该方法的表现不佳，往往需要在前端增加强制性的枝剪来控制问题规模。

技术实现要素：

为了克服现有多假设跟踪方法效率低的不足，本发明提供一种基于蒙特卡洛树搜索的多假设跟踪方法。该方法首先对顶点进行预处理，其次构建蒙特卡洛树搜索(mcts)涉及的搜索树，再驱动mcts进行搜索，最后进行结果搜集。本发明为tomht提供了在问题规模较大时替代经典的精确算法的技术方案，能够显著提升运算效率。相比背景技术方法它的最大优势在于能够任意的控制运算时间，并且尽可能的给出优秀的近似解。

本发明解决其技术问题所采用的技术方案：一种基于蒙特卡洛树搜索的多假设跟踪方法，其特点是包括以下步骤：

步骤一、对顶点进行预处理，首先归一化各个顶点的权值，用一个新的权值向量w′来取代原本的权值向量w，w＝{w1,w2,...,wm}：

然后为各个节点添加一个次级权，形成一个额外的权值向量：

其中，i(·)是指示函数，z是向量z中的元素。

步骤二、构建蒙特卡洛树搜索涉及的搜索树，树上的每个节点储存的信息包含：当前解、该节点被访问的次数和该节点的总得分。用v′表示某个节点，v表示其父节点，当前解、该节点被访问的次数和该节点的总得分分别用s(v′)，n(v′)，q(v′)表示，其中s(v′)是一个三值的向量，每个元素取0，1或者空，分别表示对应位置的节点没有选中，选中以及待定。搜索树初始化：产生一个根节点，它的s为元素全是空的m阶向量，n＝0，q＝0。

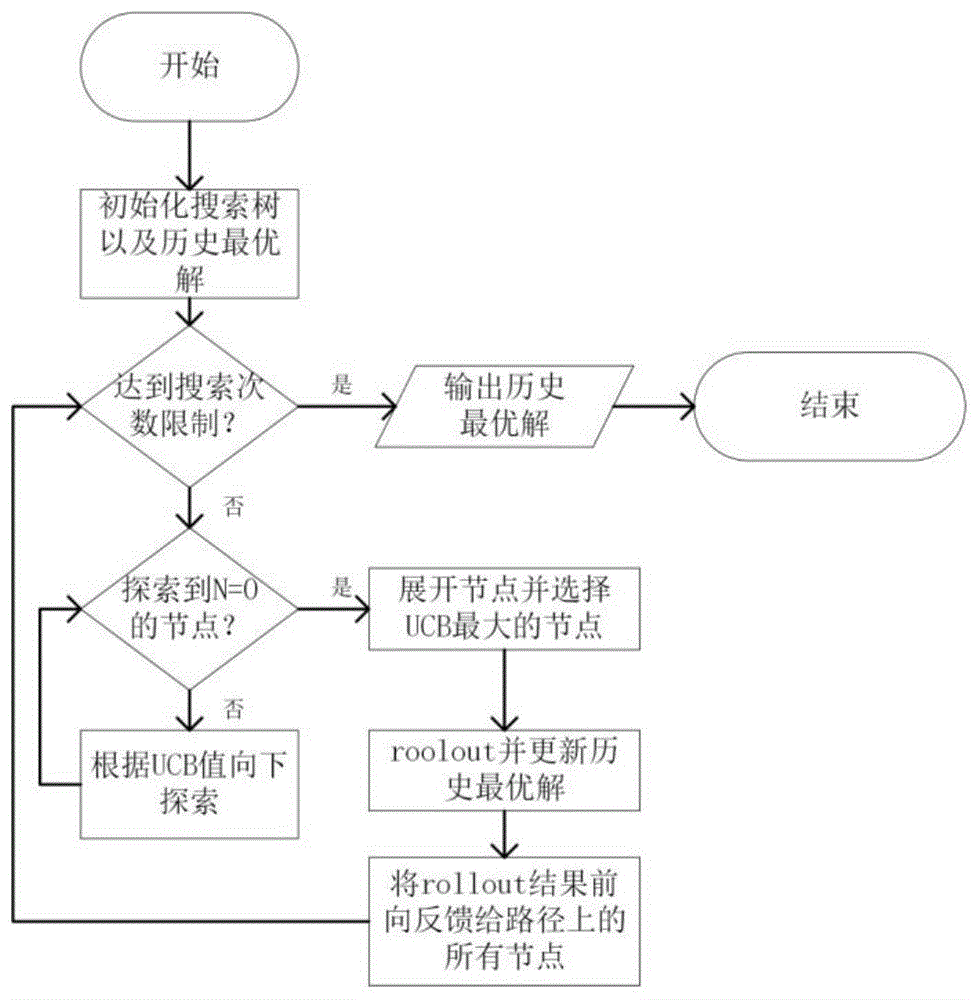
步骤三、驱动mcts进行搜索。mcts运行过程中涉及到三个操作，当前树的探索与展开、试运行以及rollout结果的前向传播。在搜索开始前还需要定义并初始化储存历史最优解的变量qbest＝0，sbest＝0。

步骤3.1、探索与展开当前树。算法每次探索当前的树时，都会从顶部的根节点出发，向下选择。如果探索到的节点已经被展开过，则选择其子节点中上置信心界最大的进行选择，对于ucb的计算公式需要重新设计。

其中，n(v)表示该节点的父节点被访问的次数，s(v′)k表示当前节点的s向量的第k项，c1，c2是两个超参数，用以权衡各项对ucb值的影响程度，c1＝1，c2＝0.05。如果探索到的节点没有被探索过，则需要展开该节点下的所有合法子节点，并且计算相应ucb值，选择ucb最大的节点，然后进行模拟。

步骤3.2、试运行。模拟的意义在于放弃对mct的向下探索，从当前解出发，按照简单的准则快速rollout，采用的准则是每次随机向解s中待定的节点中某一个置1，并将无法与该节点兼容的节点置0，直到s中所有的元素均为0或者1，此时这就是最大团问题的一个合法的团，此次rollout的质量评价q＝s*w^t，该质量评价会与历史最优质量qbest比较，如果q＞qbest，则将qbest，sbest更新为此次rollout的q和s，否则不更新历史最优值。

步骤3.3、前向传播结果。在每次rollout结束后需要把该次rollout的结果前向传递给mct中探索路径下的所有节点，更新它们的q，n值，对于路径上的任意节点v'，其更新规则为：

q＝q+q,n＝n+1

由于这个变化下次搜索每个节点的ucb值都需要重新计算。

步骤四、结果搜集。对于最大团的近似算法来说，需要在有限的时间内获得尽量可靠的结果，设置一个搜索次数的限制，当算法运行到设置的搜索次数上限，从历史最优解上搜集到算法的运行结果。

本发明的有益效果是：该方法首先对顶点进行预处理，其次构建蒙特卡洛树搜索(mcts)涉及的搜索树，再驱动mcts进行搜索，最后进行结果搜集。本发明为tomht提供了在问题规模较大时替代经典的精确算法的技术方案，能够显著提升运算效率。相比背景技术方法它的最大优势在于能够任意的控制运算时间，并且尽可能的给出优秀的近似解。

下面结合附图和具体实施方式对本发明作详细说明。

附图说明

图1是本发明基于蒙特卡洛树搜索的多假设跟踪方法的流程图。

图2是本发明方法搜索结果随着搜索次数向精确解逼近的过程曲线。

具体实施方式

参照图1-2。本发明基于蒙特卡洛树搜索的多假设跟踪方法具体步骤如下：

设最大团问题涉及的图为无向图g＝(v,e)，其中v表示顶点集v＝{v1,v2,...,vm}，m为顶点个数，e表示边集e＝{<vi,vj>|i≠j,vi∈v,vj∈v}。描述一个最大团问题需要邻接矩阵和顶点的权值向量，其中邻接矩阵表示为

权值向量表示每个顶点的权值w＝{w1,w2,...,wm}。最大团问题的目标是寻找一个v的子集v'，子集中所有的顶点都是两两连通的，最大化v'中所有顶点的总权值就是最大团问题。

步骤1，对顶点进行预处理，首先归一化各个顶点的权值，用一个新的权值向量w’来取代原本的w

然后为各个节点添加一个次级权，形成一个额外的权值向量：

其中i(·)是指示函数，z是向量z中的元素。

步骤2，构建蒙特卡洛树搜索(mcts)涉及的搜索树，树上的每个节点储存的信息包含：当前解、该节点被访问的次数、该节点的总得分。如果用v′表示某个节点，v表示其父节点，上诉的三个信息分别用s(v′)，n(v′)，q(v′)表示，其中s(v′)是一个三值的向量，每个元素可以取0，1或者空，分别表示对应位置的节点没有选中，选中以及待定。搜索树初始化：产生一个根节点，它的s为元素全是空的m阶向量，n＝0，q＝0。

步骤3，驱动mcts进行搜索。mcts运行过程中涉及到三个主要的操作，当前树的探索与展开，试运行(rollout)，以及rollout结果的前向传播。在搜索开始前还需要定义并初始化储存历史最优解的变量qbest＝0，sbest＝0。

子步骤1，探索与展开当前树。算法每次探索当前的树(以后称为mct)时，都会从顶部的根节点出发，向下选择。如果探索到的节点已经被展开过，则选择其子节点中上置信心界(ucb)最大的进行选择，对于本问题ucb的计算公式需要重新设计。

其中n(v)表示该节点的父节点被访问的次数，s(v′)k表示当前节点的s向量的第k项，c1，c2是两个超参数，用以权衡各项对ucb值的影响程度，在本算法中推荐值是c1＝1，c2＝0.05。如果探索到的节点没有被探索过，则需要展开该节点下的所有合法子节点，并且计算相应ucb值，选择ucb最大的节点，然后进行模拟。对于一颗mct，每次探索过程中总会遇到后者这种情况。

子步骤2，试运行(rollout)。模拟的意义在于放弃对mct的向下探索，从当前解出发，按照某些简单的准则快速rollout，对于本算法采用的准则是每次随机向解s中待定的节点中某一个置1，并将无法与该节点兼容的节点置0，直到s中所有的元素均为0或者1，此时这就是最大团问题的一个合法的团，此次rollout的质量评价q＝s*w^t，该质量评价会与历史最优质量qbest比较，如果q>qbest，则将qbest,sbest更新为此次rollout的q和s，否则不更新历史最优值。

子步骤3，前向传播结果。在每次rollout结束后需要把该次rollout的结果前向传递给mct中探索路径下的所有节点，更新它们的q，n值，对于路径上的任意节点v'，其更新规则为：

q＝q+q,n＝n+1

由于这个变化下次搜索每个节点的ucb值都需要重新计算。

步骤4，结果搜集。理论上搜索的过程可以一直进行下去，对于最大团的近似算法来说，需要在有限的时间内获得尽量可靠的结果，因此算法需要设置一个搜索次数的限制，理论上搜索次数越多耗时越多，解也越接近理论最优解。当算法运行到设置的搜索次数上限，可以从历史最优解上搜集到算法的运行结果。

对于一个多目标跟踪场景，部署一个tomht跟踪器的方法没有变化，本方法作用于tomht经过聚簇之后寻找全局最优假设的步骤。为了使用本方法，在获取聚簇结果并且生成最大团问题的邻接矩阵之后，增加一个选择最大团算法的判断策略，该策略有两个方案，其一是根据经验为邻接矩阵的规模(维度与边密度)设置一个阈值，超过阈值则放弃patric的方法转而选择本方法；其二是设置一个单次运算的时间上限，当patric的方法在设置的时间内无法返回结果时换用本方法。完成了该策略之后，可以将发明技术方案中的方法直接应用于tomht生成的最大团问题中，注意到本发明得到的解不能保证是全局最优的，它是一个随着算力投入不断逼近全局最优解的方法。

为了测试本方法的效果，模拟一个最大团问题。作为一个近似算法，最重要的性能指标是其获得的解有多接近精确解，对于一个包含80节点，每个节点和其他任意一个节点相连的概率为0.4的最大团问题，每个节点权值是[0,10]上均匀分布的随机数。本发明随着搜索次数收敛到精确解到过程如图2，在接近第1500次搜索后收敛到了精确解。搜索次数对本发明的效果是有影响的，增加搜索次数意味着投入更多的算力，也能得到更好的效果。如果用近似解和精确解的相对误差来评价近似解的质量的话，对于前文中同等规模的问题进行100次蒙特卡洛实验统计平均相对误差，1000次搜索的平均相对误差为5.9％，2000次搜索的平均相对误差为3.9％。