一种基于遗传算法的近邻传播聚类方法与流程

本发明应用背景为数据挖掘技术，即从数据中挖掘知识。

技术实现要素：
是指在数据的海洋中运用聚类算法对数据进行聚类，分析聚类结果，发现或获取有用信息，其旨在克服近邻传播聚类算法对偏向参数和阻尼因子的敏感问题，提高聚类算法的准确率，属于数据挖掘机技术领域最重要的组成部分之一。

背景技术：

聚类分析（clusteranalysis）简称聚类（clustering），是把一个数据对象划分成子集的过程。每一个子集是一个簇，使得簇中的对象彼此相似，但与其他簇中的对象不相似。目前，聚类分析已经在商务智能、图像模式识别、web搜索和数字医疗等方面得到广泛应用。

聚类是一种不需要提供类标号的无监督学习方式。目前数据聚类比较典型的算法有k-means聚类、层次聚类、fcm聚类等。但是上述几种算法均存在不同程度上的缺点，如k-means聚类算法对离群点、孤立点和初始聚类中心敏感，聚类数目需要人为设定且容易陷入局部最优解等缺点；层次聚算法的树形视图不会真正将数据拆分成不同的组，且计算量非常大，算法的运行速度慢等缺点；fcm聚类对初始聚类中心敏感，容易陷入局部最优解，且计算量非常大等缺点。

2007年frey和dueck提出了一种全新的基于代表点的聚类算法ap（affinitypropagation）近邻传播聚类算法，该算法采用消息传递得到问题的解。虽然ap聚类算法几乎优于其他聚类算法，但也存在对偏向参数和阻尼因子敏感的问题。针对这一问题，王开军等提出了自适应传播聚类算法（a_ap）；xian-huiwang提出了基于粒子群智能算法自适应搜索最佳的偏向参数(paap);b.jia提出了基于布谷鸟智能算法自适应搜索最佳的偏向参数(caap)。上述方法虽然在一定程度上使得算法得到优化，但是无法精确获得全局最优解。基于遗传算法的近邻传播聚类方法是通过运用遗传算法不断的更新迭代获取最佳偏向参数和阻尼因子，ap聚类算法再根据获得的最佳偏向参数和阻尼因子完成聚类，获得最佳聚类效果。新的聚类算法不仅可以克服原算法对偏向参数和阻尼因子的敏感问题，还可以提高算法的聚类效果。

发明内容

ap聚类算法中有两个重要参数：置于相似度矩阵s(similarity)对角线的偏向参数和迭代中针对吸引度矩阵r(responsibility)和归属度矩阵a(availability)更新的阻尼因子。由于值的选取直接影响到聚类数目的多少，当较大，聚类数目就越多；反之，聚类数目就会越少。然而，大小的选择不仅决定了算法的收敛性，而且当算法发生震荡时，可以通过手动增大的值消除震荡。原始的ap聚类算法对于和大多取经验值，因此为了解决这一问题，提出一种基于遗传算法的近邻传播聚类方法,称ga_ap。该方法首先是选用遗传算法利用ap聚类算法不停地更新迭代获取适应度函数值（fitness），选用作为适应度函数，根据适应度函数值自动调整偏向参数和阻尼因子；然后将获取到的最佳和在ap聚类算法中进行聚类，完成聚类并获得最终的聚类结果。为实现上述目的，本发明采用以下技术方案：

基于遗传算法的近邻传播聚类算法主要包括以下几个部分：第一，数据预处理，即数据缺失值和数据标准化等；第二，选用遗传算法获取最优偏向参数和阻尼因子；第三，选用最优的偏向参数和阻尼因子完成ap聚类，获取最终聚类结果。

数据预处理。数据缺失值是选用和给定元组所属的类的所有样本的属性均值进行填充；数据标准化采用零均值规范化，即经过处理的数据的均值为0，标准差为1。

获取最优偏向参数和阻尼因子。将偏向参数和阻尼因子作为两个决策变量，选用ari作为适应度函数fitness，利用ap聚类算法返回适应度函数值，遗传算法通过选择、交叉和变异三个主要步骤不停地更新迭代，自动调整和，最终选取fitness函数值最大的两个决策变量作为最优偏向参数和阻尼因子。

ap聚类。利用最优偏向参数和阻尼因子在ap聚类算法中完成聚类，获取最终聚类结果。

附图说明

图1为本发明说明书附图。

图2为本发明ga_ap聚类算法流程。

图3为本发明给定偏向参数和阻尼因子范围利用遗传算法寻找最优解。

图4为本发明五种算法在5个uci数据集上的聚类数目柱状图。

图5为本发明五种算法在5个uci数据集上的f1_score曲线图。

图6为本发明五种算法在5个uci数据集上的准确率曲线图。

具体实施方式

附图中，相同部分在不同的视图中采用相同的标号表示，并且所描述的各种元件不必按照比例绘制，下面结合附图和实施例对本发明进一步说明。

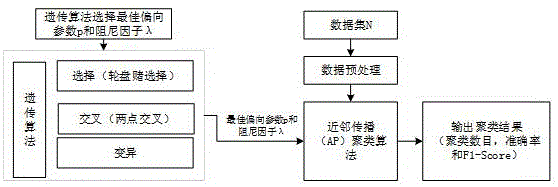
图1为说明书框图，是整个聚类算法的系统框图。

图2为本发明ga_ap聚类算法流程图。数据预处理。数据缺失值是选用和给定元组所属的类的所有样本的属性均值进行填充；数据标准化采用零均值规范化。公式为

(1)

其中表示原始数据均值，表示原始数据的标准差。选择偏向参数取值范围为，其中p_mean表示相似度矩阵的均值，阻尼因子取值范围为。设置遗传代数为numofgen=100，种群个数为numofind=30，交叉概率为pc=0.7，变异概率为pm=0.02。适应度函数fitness，选用调整兰德指数ari，即fitness=ari。调整兰德指数通过labels_true（真实类标号）和predict_labels（聚类结果后的类标号）之间的一致性来评价被聚在一起的数据对象是否被正确分类。计算公式为

(2)

式中，表示labels_true和predict_labels的一致性。选用偏向参数和阻尼因子作为决策变量，初始化种群，采用二进制编码，然后再解码，将种群个体的值作为ap聚类算法的输入计算适应度函数的值。ap聚类。设有数据集，利用数据i和k之间的负欧氏距离作为相互之间的相似度信息，即。数据对象之间的信息是利用归属度矩阵和吸引度矩阵不断更新迭代完成的，其中是指数据对象k向数据对象i发送的信息值，表示为数据对象i选择数据对象k作为代表点的合适程度；是数据对象i向数据对象k发送的信息值，表示为数据对象k作为数据对象i聚类中心点的合适程度。吸引度矩阵为

(3)

归属度矩阵为

(4)

为了防止震荡，引入了阻尼因子增强算法的稳定性，计算公式为

(5)

(6)

根据上述式子不断更新迭代吸引度矩阵和归属度矩阵，使得目标函数值最大，目标函数公式为

(7)

式中，表示聚类中心，是惩罚项，定义为

(8)

z表示所有数据对象到各自聚类中心的相似度之和。不断地更新迭代归属度和吸引度，直到达到终止条件。迭代结束后，通过计算a+r的值来确定聚类中心点。当，数据对象k为聚类中心点，各数据对象的聚类中心点计算公式为

(9)

最后，将其他数据对象分配到离它最近的聚类中心所属的类，完成聚类并返回ari的值作为适应度函数值。第一代，采用轮盘赌进行选择。每一轮将产生一个[0,1]均匀随机数，将随机数作为选择指针来确定被选个体；采用两点交叉。两个交叉位置可无重复地随机选择，在交叉点之间的变量间续地相互交换，产生两个新的后代，在在第一位置与第一个交叉点之间的一段不做交换；然后变异。重新计算种群的适应度函数值，并记录当代最优个体的染色体和最优种群个体适应度函数值。重复上述步骤，直到第100代，算法结束，选择出最优种群个体适应度函数值和决策变量值，即输出最优偏向参数和阻尼因子。然后再将最优偏向参数和阻尼因子在ap聚类算法中完成聚类，输出最终聚类结果。由于准确率和f1_score能够更加客观的反映聚类算法的优劣，accuracy和f1_score值越大说明聚类效果越好，因此选择accuracy和f1_score作为算法的评价指标。准确率,用于比较获得标签和数据提供的真实标签。计算公式为

(10)

式中，tp将正类预测为正类数，tn将负类预测为负类数，fp将负类预测为正类数误报，fn将正类预测为负类数→漏报。f1_score是由精确率（precision）和召回率(recall)共同表示。计算公式为

(11)

式中，。

图3为本发明给定偏向参数和阻尼因子范围利用遗传算法寻找最优解。偏向参数的取值范围为，其中是指相似度矩阵的均值。阻尼因子的取值范围为。利用iris数据集为例，从图中可以看出，遗传算法最大遗传代数为100代，在第89代时，适应度函数取最大值fitness=0.67，在此处获得了最优偏向参数p=-52.32，阻尼因子。

图4为本发明五种算法在iris、wine、heart、haberman和soybean-small5个uci数据集上的聚类数目柱状图。ap、a_ap、paap、caap和ga_ap五种聚类算法在5个uci数据集上的聚类数目对比。从聚类数目上看，ga_ap算法的聚类数目更接近真实数据集类数。

图5为本发明五种算法在iris、wine、heart、haberman和soybean-small5个uci数据集上的f1_score曲线图。ap、a_ap、paap、caap和ga_ap五种聚类算法在5个uci数据集上的f1_score对比。从f1_score上看，ga_ap算法的f1_score大多优于其他几种算法。

图6为本发明五种算法在iris、wine、heart、haberman和soybean-small5个uci数据集上的准确率accuracy曲线图。ap、a_ap、paap、caap和ga_ap五种聚类算法在5个uci数据集上的准确率对比。从准确率上看，ga_ap算法的准确率比其他几种算法要高。