一种渗透破坏离散元模拟方法与流程

本发明属于渗透破坏模拟技术领域，具体涉及一种渗透破坏离散元模拟方法。

背景技术：

在当前的离散元软件中，多采用流固耦合方法模拟渗透破坏时的颗粒运动，该方法虽然接近实际的渗透破坏物理过程，但其计算量大，计算效率较低，模拟计算用时较长，因此需寻求合理的简化方法对该模拟进行简化，以提高渗透破坏模拟计算的效率。

技术实现要素：

本发明的目的是提供一种渗透破坏离散元模拟方法，以解决上述技术问题。

本发明提供了一种渗透破坏离散元模拟方法，包括：

在无流体的固体颗粒模拟中，施加一种与流场水力梯度相关的力，即梯度力，用以替代流体对于颗粒的作用力，以对渗透破坏现象进行简化模拟。

进一步地，所述渗透破坏离散元模拟方法具体包括如下步骤：

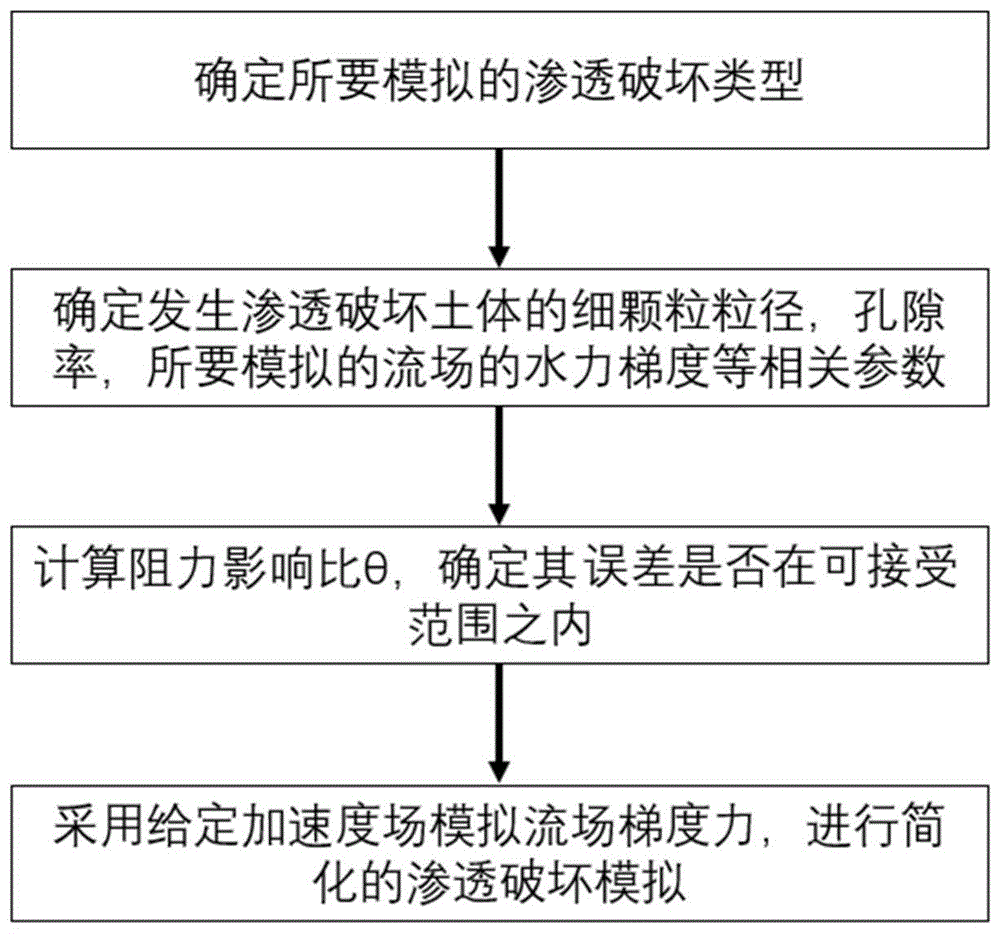
步骤1，确定所要模拟的渗透破坏类型；

步骤2，确定发生渗透破坏土体的细颗粒粒径、孔隙率，以及所要模拟的流场水力梯度；

步骤3，计算阻力影响比，确定其误差是否在可接受范围之内；

步骤4，采用给定加速度场模拟流场梯度力，进行简化的渗透破坏模拟。

进一步地，步骤3中基于下述公式计算阻力影响比θ：

式中：ρw为流体密度；r为颗粒半径；为颗粒运动速度；cd为拖曳力系数；为拖曳力修正表达式。

其中，即为标准拖曳力计算公式，为：

进一步地，步骤4中基于下述公式施加沿流线方向的加速度场，从而实现施加流场梯度力：

式中：αi为待施加的沿流线方向的加速度；γw为流体容重；γs为颗粒容重；i为待施加的水力梯度。

与现有技术相比本发明的有益效果是：

能够在实现流固耦合效果的基础上，省略流固耦合计算过程，提高模拟计算速度。

附图说明

图1是本发明一种渗透破坏离散元模拟方法的流程图；

图2为本发明一实施例中孔隙率参数为疏松时θ～r的敏感度影响曲线；

图3为本发明一实施例中孔隙率参数为普通时θ～r的敏感度影响曲线；

图4为本发明一实施例中孔隙率参数为密实时θ～r的敏感度影响曲线；

图5为本发明一实施例中细颗粒粒径为疏松时θ～i的敏感度影响曲线；

图6为本发明一实施例中细颗粒粒径为普通时θ～i的敏感度影响曲线；

图7为本发明一实施例中细颗粒粒径为密实时θ～i的敏感度影响曲线。

具体实施方式

下面结合附图所示的各实施方式对本发明进行详细说明，但应当说明的是，这些实施方式并非对本发明的限制，本领域普通技术人员根据这些实施方式所作的功能、方法、或者结构上的等效变换或替代，均属于本发明的保护范围之内。

在岩土工程常见的渗透破坏模拟中，人们主要聚焦于颗粒在流体作用下的受力，进而分析其可能发生渗透破坏的状态与特征。针对渗透破坏的流固耦合模拟，本实施例提出了一种简化的思路，并对其进行了分析验证。

当前离散元模拟中，多采用如下控制方程表征颗粒在流场中与流体耦合的受力状态：

其中：为颗粒的运动速度，m为颗粒质量，为作用在颗粒上的附加力(外部施加的力和接触力)的总和，为水力梯度产生的力，为重力引起的加速度。

对于该公式，本实施例将其转化为用各项力表征的公式，即为：

可以认为，对于任一颗粒，其在流场作用下所受到的合力由三部分组成，分别为：作用在颗粒上的附加力(外部施加的力和接触力)的总和流体作用施加在颗粒上的力重力

因此，相对于传统的纯固体离散元研究，流固耦合模拟的重点在于准确地模拟出流体对于颗粒的作用力的效果。在渗透破坏过程中，流体对任一颗粒作用力主要为沿流线方向的渗流场力受流固界面因速度差异产生的拖曳力并且在孔隙介质中，拖曳力相对较小。

本实施例提出了一种简化方法：在无流体的固体颗粒中，施加一种与流场水力梯度相关的力(以下称为梯度力)，用以替代流体对于颗粒的作用力从而在达到模拟流固耦合效果的同时减少耦合步骤，提高模拟运算效率。

根据本方案的模拟对象。依照图1所示步骤进行该模拟方法的适用性判定，当达到模拟对象的误差允许范围之内时，即可采用该简化模拟方法对渗透破坏现象进行简化模拟。

在上文的推导与分析中，利用离散元开展流固耦合模拟的目的即是正确反映流体对于颗粒的作用力。

以管涌现象为例，定义阻力影响比θ，有：

由上，θ表征了颗粒所受拖曳力在其受到流体作用力中的占比，即阻力对于流体对颗粒作用力的影响程度，即使用该简化方案所带来的相对误差大小。

针对该分析中的部分参数，其取值表如下：

为了更加简化地分析各项不确定参数与θ的响应关系，此处引入如下两个关系：

(1)darcy公式

其中，为该流场中流体的流速，k为该土体的渗透系数，i为该流场的水力梯度。

(2)kozeny-carman公式

其中，k为渗透系数，s0为颗粒单位体积的比表面积，∈为土体孔隙率。

对于离散元模拟中形状概化为标准球形的颗粒，可通过如下公式计算其单位体积的比表面积：

所以原式变为：

由上文中分析得到的各控制方程，我们需进行阻力影响比θ分别与颗粒半径r，颗粒运动速度以及水力梯度i之间的响应关系。

根据上文分析，最终联立得到阻力影响比θ的最终公式：

考虑到该方案是对传统流固耦合模拟中复杂情况的一些简化，因此需要通过对其误差进行分析来验证其有效性。

可以看出，在结合前文给出的关系，阻力影响比θ主要受如下三个参数的影响：粒径r、水力梯度i、孔隙率∈。

对于孔隙率∈，土体试样在受到流体冲蚀而发生管涌现象时，其孔隙率的不同将会导致不同的管涌破坏后果，因此针对不同孔隙率的土体试样进行研究非常有必要。根据传统渗透破坏研究的试样调查，我们在此次误差分析中分别选取孔隙率参数为0.1(密实)，0.35(普通)，0.5(疏松)三种状态进行分析。

1、粒径r

针对管涌现象，其为在渗流场的作用下，一定级配的无黏性土中的细小颗粒通过较大颗粒形成的孔隙发生移动而产生破坏。本实施例中着重分析无黏性土中的细小颗粒受力情况。此处主要考虑粒径在0.06-2mm的土体颗粒。

根据图2、图3、图4可以看出，在较大范围的水力梯度作用下，三种密实程度(分别为密实、正常、疏松)的试样，采用该简化方法所带来的误差，即阻力影响比θ随细颗粒粒径的变化，均保持在0.05％～0.4％之间，这符合渗透破坏现象模拟的误差要求，因此该方法具有较强的有效性。

2、水力梯度i

根据目前的实验以及数值模拟采用数据，对于具体产生管涌现象水力梯度没有较为明确的范围规定。本实施例采取一个较大的水力梯度分析范围，即i＝1～20进行参数的敏感度分析。

根据图5、图6、图7可以看出，在给定细颗粒粒径的范围内，三种密实程度(分别为密实、正常、疏松)的试样，采用该简化方法所带来的误差，即阻力影响比θ随流场水力梯度的变化，亦保持在0.05％～0.4％之间，这符合渗透破坏现象模拟的误差要求，因此该方法具有较强的有效性。

对于本领域技术人员而言，显然本发明不限于上述示范性实施例的细节，而且在不背离本发明的精神或基本特征的情况下，能够以其他的具体形式实现本发明。因此，无论从哪一点来看，均应将实施例看作是示范性的，而且是非限制性的，本发明的范围由所附权利要求而不是上述说明限定，因此旨在将落在权利要求的等同要件的含义和范围内的所有变化囊括在本发明内。