一种月地三脉冲返回轨道速度增量分析方法与流程

本发明属于月地返回轨道特性解析分析领域，特别涉及一种月地三脉冲返回轨道速度增量分析方法。

背景技术：

月球是人类探测太空奥秘的首选目标，也是人类为扩大生存空间进入深空最合适的中转站，所以人类也在不断努力探索各种登陆月球的方式。随着嫦娥四号任务的圆满成功，越来越多的人憧憬中国载人登月梦想能够尽早实现。

21世纪初，美国公布的“星座”计划中具体阐述了全月面到达和任意时刻返回的任务目标，全月面到达便要求探测任务具备对月球高纬地区开展月面活动的能力，而任意时刻返回则是为了保障航天员的安全。

载人登月任意时刻返回方式主要有两种类型：第一种是航天器不通过轨道机动，沿着原飞行轨道自由返回地球，这种方式只适用于地月转移阶段，而关于自由返回轨道的研究也已经比较成熟。第二种是航天器通过轨道机动返回地球，这种方式适用载人登月各个阶段。

在环月飞行阶段，由于出发轨道面的指向可能并不理想，载人登月任务若要在任意时刻做到安全返回，必须通过轨道机动实现。航天器在环月飞行过程中，一旦发生故障需要应急返回时，往往需要施加额外的速度来调整轨道面以进入返回窗口。调整轨道面通常有两种方案，分别是单脉冲变轨和三脉冲变轨。

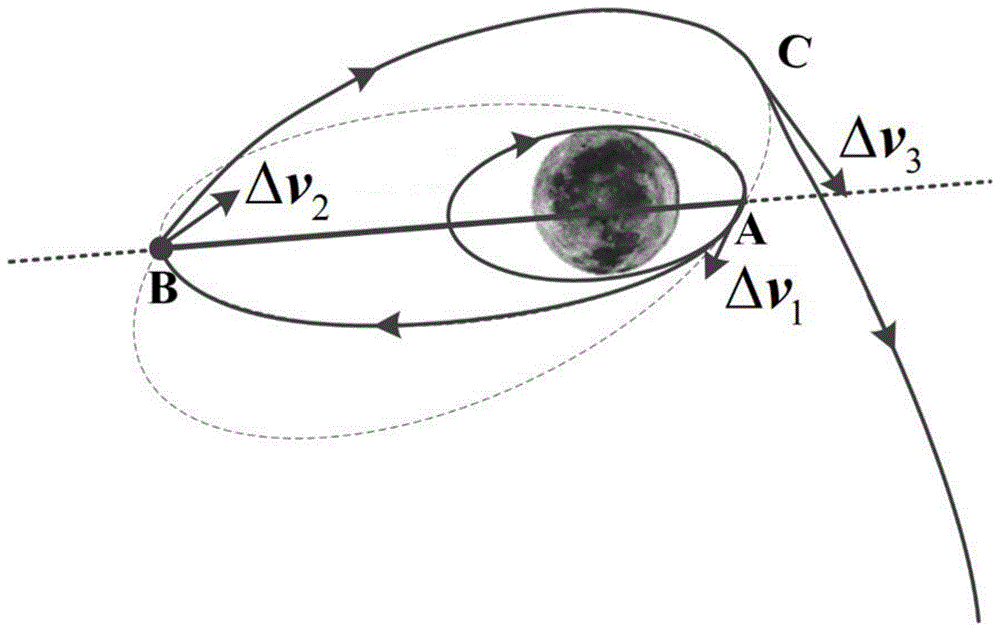
如图1所示为月地三脉冲返回轨道示意图。月地三脉冲返回轨道机动方案具体过程如下：首先，在环月轨道施加第一次切向脉冲δv1，进入大椭圆过渡轨道，施加脉冲处的点a同时也是大椭圆过渡轨道的近月点。然后，在大椭圆过渡轨道上的某点(点b)施加第二次脉冲δv2，调整轨道面角度，点b的位置由环月轨道面和月球逃逸轨道面的交线确定，且点b为离大椭圆过渡轨道远月点较近的交点。最后，在大椭圆过渡轨道的近月点(点c)的切线方向施加第三次脉冲δv3，进入月球逃逸轨道返回地球。

在轨道面角度调整过大时，与单脉冲变轨相比，三脉冲变轨可以有效减少轨道机动所需的速度增量，适应性更强，因此一般作为环月飞行段任意时刻返回的轨道机动方案。

关于月地返回轨道的设计与分析方法，通常采用以下几类动力学模型：圆锥曲线拼接模型、多圆锥截线法、限制性三体模型和高精度模型。

在后续的载人登月工程中，尤其关注燃料消耗的问题，由于速度增量直接反映航天器的燃料消耗，所以有必要对轨道方案中的速度增量特性进行计算分析。

但是，在对月地三脉冲返回轨道速度增量进行初步分析时，采用上述现有技术中的动力学模型进行求解，虽然精度较高，但由于需要考虑一些摄动项(如地球中心引力、日月引力摄动、地球和月球非球形引力摄动、太阳光压摄动等)，因而求解过程比较复杂，轨道积分计算的速度慢，导致计算用时较长，并不适合作为一种速度增量初步分析的工具。

技术实现要素：

本发明的目的在于，针对现有技术中分析月地三脉冲返回轨道速度增量时求解复杂、速度慢的缺点，提供一种月地三脉冲返回轨道速度增量分析方法，利用空间几何关系，能够快速有效、直观简洁地对三脉冲机动过程所需的速度增量进行初步近似分析。

为解决上述技术问题，本发明所采用的技术方案是：

一种月地三脉冲返回轨道速度增量分析方法，其特点是包括以下步骤：

步骤a，以月心为原点，获得环月轨道面法向单位矢量h1，月球逃逸轨道面法向单位矢量h2，施加第一次脉冲的位置ra，施加第二次脉冲的位置rb，施加第三次脉冲的位置rc；

步骤b，获得以月球逃逸轨道瞄准v∞out为轴线的圆锥面s1，其中圆锥面s1对应的圆锥的半锥角为η；

步骤c，以v∞out和h1所在的平面为基准面，设定rc绕v∞out所在直线旋转的角度σ，根据σ确定rc；再根据v∞out和rc确定月球逃逸轨道面；

步骤d，获得以rc所在直线为轴线的圆锥面s2，圆锥面s2对应的圆锥的半锥角为α；

步骤e，获得h1与v∞out的夹角β，环月轨道与月球逃逸轨道的异面差ξ，且ξ为h1与h2的交角；

步骤f，

按照下式求得第一次脉冲大小δv1：

其中，μm为月球引力常数，atra为大椭圆过渡轨道的半长轴且ttra为大椭圆过渡轨道的周期；

按照下式求得第二次脉冲大小δv2：

其中，vτ2为施加第二次脉冲前rb处的横向速度且其中htra为大椭圆过渡轨道的面积速度，etra为大椭圆过渡轨道的偏心率；

按照下式求得第三次脉冲大小δv3：

其中，aleo为月球逃逸轨道半长轴且

步骤g，按照下式求得总速度增量δv：

δv＝δv1+δv2+δv3；

步骤h，改变影响总速度增量δv大小的自变量，获得总速度增量随自变量变化的规律。

作为一种优选方式，所述步骤h中的自变量包括σ、β、v∞out中的一种或几种。

作为一种优选方式，所述步骤h还包括：对σ进行数值寻优以得到总速度增量δv的最小值。

与现有技术相比，本发明利用空间几何关系，能够快速有效、直观简洁地对三脉冲机动过程所需的速度增量进行初步近似分析，可以作为后续载人登月探测任务返回轨道方案中燃料消耗的初步分析工具。

附图说明

图1是月地三脉冲返回轨道示意图。

图2是双曲剩余速度锥面示意图。

图3是本发明所涉参数的空间几何关系示意图。

图4是总速度增量与ξ和α的关系图。

图5是总速度增量与σ的关系图。

图6是不同β对应的最小总速度增量图。

具体实施方式

本发明以双曲剩余速度锥面为基础，如图2所示，双曲剩余速度锥面定义如下：

在二体模型下，航天器在月球影响球内的飞越轨道为双曲线轨道。航天器在月球影响球边界处的速度可以看作在无穷远处的速度，即双曲线轨道的剩余速度v∞。航天器在进入月球影响球处的速度v∞in和飞出月球影响球时的速度v∞out大小相同，均可以视为沿着渐近线方向，渐近为δ。当v∞in和双曲线轨道近月点的月心距rp给定时，所有可能存在的v∞out分布构成一个以v∞in所在直线为轴线的圆锥面，该圆锥面称之为双曲剩余速度锥面。

如图3所示，在双曲速度锥面基础上，可以得到相关轨道参数的空间几何关系式：

以月球为中心天体(即以月心为原点)，设环月轨道面法向单位矢量为h1，月球逃逸轨道面法向单位矢量为h2，施加第一次脉冲的位置为ra，施加第二次脉冲的位置为rb，施加第三次脉冲的位置为rc。当月球逃逸轨道瞄准的v∞out给定时，所有可能存在的rc构成以v∞out所在直线为轴线的圆锥面s1，且圆锥面s1对应的圆锥的半锥角为η。以v∞out和h1所在的平面为基准面(如3中的阴影平面)，rc绕v∞out所在直线旋转的角度记为σ，当σ确定时，rc随之确定，月球逃逸轨道面进而可由v∞out和rc确定。此外，当rc给定时，所有可能存在的rb构成以rc所在直线为轴线的圆锥面s2，圆锥面s2对应的圆锥的半锥角为α。设h1与v∞out的夹角为β，环月轨道与月球逃逸轨道异面差为ξ，即h1与h2的交角为ξ。根据空间几何关系，可以得到以下关系式：

三脉冲机动过程所需的速度增量计算过程如下：

设大椭圆过渡轨道的周期为ttra，则大椭圆过渡轨道的半长轴为：

式中：μm为月球引力常数。

第一次脉冲大小δv1为：

其中，μm为月球引力常数。

月球逃逸轨道半长轴为：

第三次脉冲大小δv3为：

月球逃逸轨道的偏心率和圆锥半锥角η为：

根据异面变轨公式，可得第二次脉冲δv2大小为：

式中：vτ2为施加第二次脉冲前rb处的横向速度，可以表示为：

式中：htra为大椭圆过渡轨道的面积速度，etra为大椭圆过渡轨道的偏心率；fb为大椭圆过渡轨道上施加第二次脉冲处的真近点角。

因此，当v∞out给定时，β、η随之确定，由空间几何关系式可知，α和ξ均是关于σ的函数，则δv2可以表示为关于σ的函数。因此，可以由σ的大小直接求得对应的速度增量，也可以简单地对σ进行数值寻优，即可得到所需的最小速度增量，求解过程快速有效，同时也能根据这些角度得到对应的空间几何位置，显得直观简洁。三次机动的总速度增量δv为：

δv＝δv1+δv2+δv3；

此外，改变影响总速度增量δv大小的自变量(包括σ、β、v∞out中的一种或几种)，可以获得总速度增量随自变量变化的规律。

下面给出本发明的一具体的实施例：

初始环月轨道半径为1938km，大椭圆过渡轨道周期ttra为24小时，瞄准参数v∞out的大小为1000m/s，β为45°。

总速度增量δv与ξ和α的关系如图4所示，从图4中可以看出，δv受ξ和α影响较大，ξ越大，δv越大，α越大，δv越大

总速度增量δv与σ的关系图如图5所示，从图5中可以看出，δv随着σ的增大，呈现先减小后增大的趋势。当σ为51.7°时，δv达到最小为1119.91m/s，此时ξ为56.3°，α为14.0°。当σ为90°时，δv达到最大为1271.30m/s，此时ξ为45.0°，α为45.8°。

改变β的大小，其它参数设置不变，计算不同β对应的最小总速度增量，如图6所示。从图6中可以看出，当β逐渐增大时，三脉冲返回轨道机动需要的最小总速度增量逐渐减小，最大约为1600m/s，最小不到900m/s。这个结论可以从轨道的空间几何关系中得到解释，例如，当β为90°时，环月轨道面与月球逃逸轨道面重合时，无需调整轨道面异面差，所以需要的总速度增量最小。

可见，本发明的基于双曲剩余速度锥面的月地三脉冲返回轨道速度增量分析方法，可以作为载人登月探测任务返回轨道方案燃料消耗的一种初步分析工具，实现快速有效地分析月地三脉冲返回轨道速度增量相关特性，为后续载人登月探测任务返回轨道方案提供参考。

上面结合附图对本发明的实施例进行了描述，但是本发明并不局限于上述的具体实施方式，上述的具体实施方式仅仅是示意性的，而不是局限性的，本领域的普通技术人员在本发明的启示下，在不脱离本发明宗旨和权利要求所保护的范围情况下，还可做出很多形式，这些均属于本发明的保护范围之内。