一种基于用电负荷分析的居民用户分类方法与流程

本发明属于供电领域，具体涉及一种基于用电负荷分析的居民用户分类方法。

背景技术：

居民用户的用电负荷正在逐渐成为电网系统中的高峰负荷的主要构成部分，给电网系统的安全稳定运行带来了新的挑战。因此，如何针对各类居民用户的用电负荷特征来实现电网系统的供给侧管理，是未来电网系统安全稳定运行的关键。

针对各类居民用户的用电负荷特征的聚类分析，许多学者做过相关的研究。蔡恒，伍惠铖，邹知斌等在《某居民小区用电调查与负荷分析》(江西电力,2017,41(2):24-27，)中通过对南昌市某居民小区用户智能电表的数据进行分析，给出了用户四个季节的用电曲线，以及节假日和工作日、周末的用电曲线，分析了用户的用电行为，为用电客户、供电企业和社会环境的创新服务提供了依据。刘飞，贲树俊等在《基于聚类分析的居民典型负荷特性分析》(江苏电机工程，2007,12(26):34-37)中用k-means聚类对用电数据进行分析，得到不同季节的典型用电负荷代表曲线，研究得到居民负荷特征与各个影响因素之间的一些联系。丁麒，王光增等在《地区电力用户负荷模式聚类分析应用》(机电工程，2008,25(9):31-33,84)中对典型变电所区域的用户进行了聚类，与传统的国民经济行业分类进行了类比，该方法也在用电负荷管理、变电站规划、状态估计等方面为供电部门提供了参考依据。张倩在《供需互动的居民用户用电决策模型及信息系统研究》(学位论文：华北电力大学.2017)中利用模糊c均值聚类算法对居民负荷曲线进行聚类分析，得出居民的不同用电特征，发掘居民用电优化空间，引导用户合理用电，优化用电结构，达到削峰填谷的作用。孙毅，顾玮，李彬等在《面向售电侧改革的用户分层聚类与套餐推荐方法》(电网技术，2018,42(2):447-454)中提出了一种基于差异化特征提取的用户分层聚类方法，分层聚类中的第1层聚类基于马尔科夫模型提取代表用户行为多样性的用电特征；第2层针对第1层得到的各类用户提取差异化的用电特征，分别运用合适的聚类算法实现用户的再次分类。最后为两层聚类后的子类用户推荐合适的电价套餐。

然而，居民用户的用电负荷具有用电信息数据量大的特点，并且不同种类的居民用户的用电方式也存在较大差异，而上述方法对各类居民用户的用电负荷特征的分析的精细化程度不够，导致不能准确地按各类居民用户的用电方式对居民用户进行分类，从而使供电单位不能根据居民用户的种类确定各类居民用户的用电负荷特征，进而准确地进行电网系统的供给侧管理，保证电网系统安全稳定运行。

技术实现要素：

有效地分析各类居民用户的用电负荷特征是实施电网系统的供给侧管理措施的基础。通过对各类居民用户的用电负荷特征的分析，不仅有助于评价一个地区用电负荷构成、用电模式的优劣，它也是合理安排用电布局、有效利用电能资源的一项重要研究性工作，能够保障电网系统安全、稳定地运行。

本发明的目的在于提供一种根据居民用户的日用电负荷曲线获取的居民用户分类方法，从而能够根据居民用户的种类确定各类居民用户的用电负荷特征，进而准确地进行电网系统的供给侧管理，保证电网系统安全稳定运行。

为实现上述目的，本发明采用了如下技术方案：

本发明提供了一种基于用电负荷分析的居民用户分类方法，具有这样的特征，包括以下步骤：

步骤s1：对多个日用电负荷数据进行数据预处理，获取多个样本数据；

步骤s2：对样本数据进行预聚类，获取多个数据子簇；

步骤s3：基于贝叶斯准则对数据子簇进行凝聚聚类，获取多个数据聚类；

步骤s4：对数据聚类进行分析计算，获取凝聚聚类的轮廓平均值；

步骤s5：判断轮廓平均值是否大于等于预定的轮廓阈值，若判断为是时，进入步骤s10，若判断为否时，进入步骤s6；

步骤s6：判断凝聚聚类的次数是否小于等于预定聚类次数，若判断为是时，进入步骤s7；

步骤s7：判断每个数据聚类中的样本数据的数量是否小于等于预定样本数量，若判断为否时，将数据聚类作为中间数据聚类，进入步骤s8，若判断为是时，将数据聚类作为已确定数据聚类，进入步骤s9；

步骤s8：根据中间数据聚类中的样本数据，重复步骤s2-s3，获取待确定数据聚类；

步骤s9：将待确定数据聚类和已确定数据聚类进行整合，获取新的数据聚类，然后进入步骤s4；

步骤s10：根据数据聚类对居民用户进行分类。

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，数据聚类的数量为m个，预定聚类次数为m次，轮廓阈值为

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，步骤s1中的数据预处理包括以下子步骤：

步骤s1-1：采用牛顿插值法对多个日用电负荷数据进行数据清洗，获取多个初始数据；

步骤s1-2：对多个初始数据分别进行数据归一化处理，获取对应的多个样本数据。

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，步骤s2包括如下子步骤：

步骤s2-1：基于birch算法逐个读取样本数据；

步骤s2-2：根据读取结果对密集区域内的多个样本数据进行预聚类，从而获取数据子簇。

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，步骤s3中的贝叶斯准则的表达式为：

bic＝-2ln(l)+ln(h)·y，

bic为数据聚类的分类评价，bic越高代表数据聚类的分类越合理，l为极大似然函数值，h为数据子簇的数量，y为所有数据子簇包含的样本数据的数量。

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，样本数据的数量为n，n为大于等于2的正整数，

步骤s4包括以下子步骤：

步骤s4-1：根据n个样本数据对应得到n个样本数据的簇内不相似度a(i)，簇内不相似度a(i)的表达式为：

i，i’为同个数据聚类内两个样本数据，dist(i，i’)为两个样本数据i，i’间的欧式距离，|cs|为样本数据i所属的数据聚类s内所包含的样本数据的数量；

步骤s4-2：根据n个样本数据对应得到n个样本数据的簇间不相似度b(i)，簇间不相似度b(i)的表达式为：

i，i’为不同的数据聚类内两个样本数据，dist(i，i’)为两个样本数据i，i’间的欧式距离，|ct|为样本数据i’所属的数据聚类t内所包含的样本数据的数量；

步骤s4-3：根据样本数据的簇内不相似度a(i)和样本数据的簇间不相似度b(i)得到轮廓平均值t，轮廓平均值t的表达式为：

s(i)为轮廓系数，表达式为：

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，步骤s10中对居民用户进行分类具体为根据多个预定用电特征指标，获取与多个数据聚类对应的居民用户分类。

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，居民用户分类包括上班族+小孩综合住户、上班族+老人综合住户、老人家庭住户、单身上班族住户以及综合类多人口住户。

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，预定用电特征指标包括整体负荷水平、用电高峰时段、晚负荷下降时点以及日负荷波动率，整体负荷水平的负荷水平值的表达式为：

plevel代表负荷水平值；paverage为日均负荷；pmax为所有日用电负荷数据的最大值，用电高峰时段包括5点至6点、11点至12点、19点至20点以及20点至21点，晚负荷下降时点包括21点和22点，日负荷波动率的表达式为：

pwave代表日负荷波动率；perror为日负荷的标准差。

在本发明提供的基于用电负荷分析的居民用户分类方法中，还可以具有这样的特征：其中，整体负荷水平包括高负荷水平、较高负荷水平、中等负荷水平、低负荷水平以及极低负荷水平，高负荷水平的负荷水平值plevel大于等于50％，较高负荷水平为负荷水平值plevel小于50％且大于等于40％，中等负荷水平为负荷水平值plevel小于40％且大于等于20％，低负荷水平为负荷水平值plevel小于20％且大于等于10％，极低负荷水平为负荷水平值plevel小于10％。

发明的作用与效果

根据本发明所涉及的一种基于用电负荷分析的居民用户分类方法，因为首先对日用电负荷数据进行数据预处理获取多个样本数据，接着对样本数据进行预聚类和凝聚聚类获取多个数据聚类，然后通过对多个数据聚类的轮廓平均值与预定的轮廓阈值进行比较判断，然后根据判断结果、凝聚聚类次数以及数据聚类中的样本数据的数量，对样本数据进行重复多次预聚类和凝聚聚类，最后根据数据聚类对居民用户进行分类，所以，本发明的一种基于用电负荷分析的居民用户分类方法基于贝叶斯准则通过对样本数据进行多次聚类形成多个数据聚类，从而能够快速地进行多个数据聚类的最优化划分，进而根据数据聚类对居民用户进行分类，相较以往的居民用户分类方法，对居民用电负荷的分析更为精细，大大提高对居民用户的分类的准确性，从而让供电单位能够根据居民用户的种类确定各类居民用户的用电负荷特征，进而准确地进行电网系统的供给侧管理，保证电网系统安全稳定运行。

附图说明

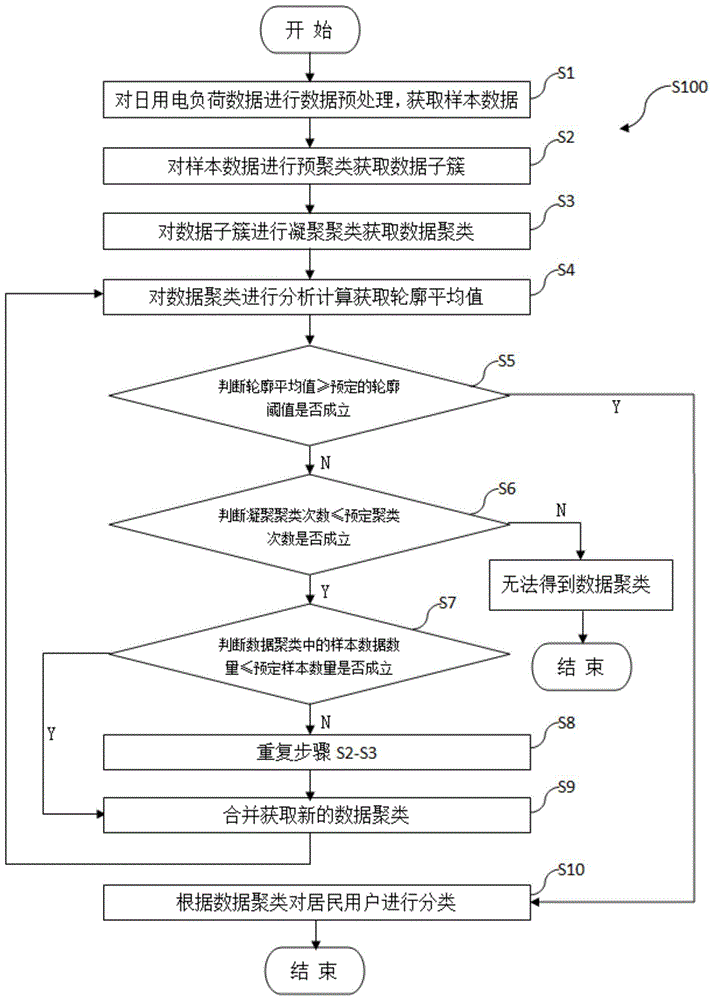
图1是本发明的实施例中的一种基于用电负荷分析的居民用户分类方法的步骤示意图；

图2是本发明的实施例中的样本数据曲线；

图3(a)是本发明的实施例中的日用电负荷数据经过第一次预聚类-凝聚聚类后形成的数据聚类结果一；

图3(b)是本发明的实施例中的日用电负荷数据经过第一次预聚类-凝聚聚类后形成的数据聚类结果二；

图4(a)是本发明的实施例中的日用电负荷数据经过第二次预聚类-凝聚聚类后形成的数据聚类结果一；

图4(b)是本发明的实施例中的日用电负荷数据经过第二次预聚类-凝聚聚类后形成的数据聚类结果二；

图5(a)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果一；

图5(b)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果二；

图5(c)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果三；

图5(d)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果四；以及

图6是本发明的实施例中的日用电负荷数据经过预聚类-凝聚聚类后完成的数据聚类结果。

具体实施方式

为了使本发明实现的技术手段、创作特征、达成目的与功效易于明白了解，以下实施例结合附图对本发明的基于用电负荷分析的居民用户分类方法作具体阐述。

图1是本发明的实施例中的基于用电负荷分析的居民用户分类方法的步骤示意图。

如图1所示，本实施例中的基于用电负荷分析的居民用户分类方法，用于根据多个日用电负荷数据对居民用户进行分类，包括以下步骤：

步骤s1：对多个日用电负荷数据进行数据预处理，获取多个样本数据，在步骤s1中的数据预处理包括以下子步骤：

步骤s1-1：采用牛顿插值法对多个日用电负荷数据进行数据清洗，获取多个初始数据。

在实际采样过程中，由于硬件因素的原因，会使一部分的日用电负荷数据在采样过程中丢失，因此需要通过使用牛顿插值法对丢失的日用电负荷数据进行数据清洗以使得初始数据的数量与日用电负荷数据的数量一致。

具体过程为：对多个日用电负荷数据进行数据清洗，主要采用牛顿插值法对缺失数据进行填补，获取多个初始数据。

牛顿插值法的插值多项式为式(1)所示：

其中，n为日用电负荷数据的数量，n为大于等于2的正整数，f(xi)为牛顿插值法得到的缺失的日用电负荷数据，(x1,f(x1)),(x2,f(x2)),…,(xn,f(xn))为n个日用电负荷数据组成的数列，(xi,f(xi))为缺失的日用电负荷数据，x∈r,i∈[1,n]，p(xi)为牛顿插值逼近函数，r(xi)为误差函数。

牛顿插值逼近函数的表达式为式(2)所示：

误差函数的表达式为式(3)所示：

r(xi)＝(xi-x1)(xi-x2)…(xi-xn)f[xn,xn-1,…,x1,xi](3)

在本实施例中，日用电负荷数据为若干台区一年的日用电负荷数据，每个台区对应电网系统中的一台变压器的供电区域，日用电负荷数据的采样数量为96个(24小时，每隔15分钟采集一个点)，初始数据的数量也为96个。

步骤s1-2：对多个初始数据分别进行数据归一化处理，获取对应的多个样本数据，具体为采用线性归一化的方法，把初始数据的取值转换到[0,1]之间，获取对应的样本数据。

归一化公式为式(4)所示：

p'i＝(pi-min(p))/(max(p)-min(p))(4)

式中，i∈[1,n]。

其中，p为初始数据，pi为归一化后的数据，即样本数据。

图2是本发明的实施例中的样本数据曲线。

在本实施例中，多个初始数据来源于多个台区，而来源于不同台区之间的初始数据表示的容量是不相同的，虽然初始数据的量纲是相同的，但来源于不同台区间的初始数据大小相差悬殊。因此需要对所有初始数据进行归一化处理，即通过变换，将有量纲的初始数据转变为无量纲，即获取标量的样本数据，这样就保证了后面聚类结果的准确性。

如图2所示，利用式(4)对多个初始数据进行归一化处理，获取多个样本数据，并根据多个样本数据画出样本数据曲线。在实际应用中，不同台区得到的最大负荷(lmax)、最小负荷(lmin)是不同的，这样会造成归一化的结果不稳定，从而影响后续的结果。因此，根据各个台区负荷的实际情况，用经验值来替代lmax、lmin，这里取lmax＝500,lmin＝0，这样就避免了不同样本集的lmax、lmin不同所造成的模型偏差。

步骤s2：对样本数据进行预聚类，获取多个数据子簇，步骤s2包括如下子步骤：

步骤s2-1：基于birch算法逐个读取样本数据，具体为采用birch(balancediterativereducingandclusteringusinghierarchies，利用层次结构的平衡迭代归约和聚类)算法中cf(clusteringfeature)树生长的思想，逐个读取多个样本数据的集中数据点。

步骤s2-2：根据读取结果对密集区域内的多个样本数据进行预聚类，从而获取数据子簇，具体为在生成cf树的同时，预先聚类密集区域的样本数据，从而形成多个数据子簇。

步骤s3：基于贝叶斯准则对数据子簇进行凝聚聚类，获取多个数据聚类，数据聚类的数量为m个，贝叶斯准则的表达式为式(5)所示：

bic＝-2ln(l)+ln(h)·y(5)

bic为数据聚类评价，bic越高代表数据聚类的划分越合理，l为极大似然函数值，h为数据子簇的数量，y为所有数据子簇包含的样本数据的数量，

具体为：

以预聚类阶段的结果-数据子簇为对象，利用凝聚法(即重复地将最近的两个数据子簇进行合并形成新的数据子簇)，逐个地合并数据子簇，直到合并为期望的数据子簇数量为止，并将此时的数据子簇作为数据聚类。

预聚类-凝聚聚类即为两步法聚类，采用两步法聚类时，聚类准则基于贝叶斯准则，即为bayesianinformationcriterion(bic)。

步骤s4：对数据聚类进行分析计算，获取数据聚类的轮廓平均值，步骤s4包括以下子步骤：

步骤s4-1：根据n个样本数据对应得到n个样本数据的簇内不相似度a(i)，簇内不相似度a(i)的表达式为式(9)：

i，i’为同个数据聚类内两个样本数据，dist(i，i’)为两个样本数据i，i’间的欧式距离，|cs|为样本数据i所属的数据聚类s内所包含的样本数据的数量；

步骤s4-2：根据n个样本数据对应得到n个样本数据的簇间不相似度b(i)，簇间不相似度b(i)的表达式为式(10)所示：

i，i’为不同的数据聚类内两个样本数据，dist(i，i’)为两个样本数据i，i’间的欧式距离，|ct|为样本数据i’所属的数据聚类t内所包含的样本数据的数量；

步骤s4-3：根据样本数据的簇内不相似度a(i)和样本数据的簇间不相似度b(i)得到轮廓平均值t，轮廓平均值t的表达式为式(11)所示：

s(i)为轮廓系数，表达式为式(12)所示：

步骤s5：判断轮廓平均值是否大于等于预定的轮廓阈值，轮廓阈值为预定聚类次数为m次，即判断轮廓平均值是否成立，若判断为是时，聚类完成，进入步骤s10，若判断为否时，进入下一步，即步骤s6。

在本实施例中，预定聚类次数m等于3。

步骤s6：判断凝聚聚类的次数是否小于等于预定聚类次数，若判断为是时，进入下一步，即步骤s7，聚类终止，即无法得到聚类结果。

步骤s7：判断每个数据聚类中的样本数据的数量是否小于等于预定样本数量，若判断为否时，将数据聚类作为中间数据聚类，进入步骤s8，若判断为是时，将数据聚类作为已确定数据聚类，进入步骤s9；

步骤s7的过程具体为：

设聚类结果为存在q类数据聚类，分别对每一类数据聚类q中的样本数据的数量wq(q＝[1,q]，q∈n)进行判断，如果wq小于等于预定的样本数量，则不需要对该类聚类继续进行聚类并将数据聚类q作为已确定数据聚类q1，进入步骤s9，否则，将数据聚类q作为中间数据聚类q2，进入步骤s8。

在本实施例中，预定样本数量为2个。

步骤s8：根据中间数据聚类中的样本数据，重复步骤s2-s3，获取待确定数据聚类；

步骤s8的过程具体为：

将所有的中间数据聚类q2重复步骤s2-s3一次，获取待确定数据分类q3。

步骤s9：将待确定数据聚类和已确定数据聚类进行整合，获取新的数据聚类，然后进入步骤s4；

步骤s9的过程具体为：

将所有的待确定数据分类q3和已确定数据聚类q1进行整合，获取新的数据聚类。

图3(a)是本发明的实施例中的日用电负荷数据经过第一次预聚类-凝聚聚类后形成的数据聚类结果一；图3(b)是本发明的实施例中的日用电负荷数据经过第一次预聚类-凝聚聚类后形成的数据聚类结果二；图4(a)是本发明的实施例中的日用电负荷数据经过第二次预聚类-凝聚聚类后形成的数据聚类结果一；图4(b)是本发明的实施例中的日用电负荷数据经过第二次预聚类-凝聚聚类后形成的数据聚类结果二；图5(a)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果一；图5(b)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果二；图5(c)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果三；图5(d)是本发明的实施例中的日用电负荷数据经过第三次预聚类-凝聚聚类后形成的数据聚类结果四；图6是本发明的实施例中的日用电负荷数据经过预聚类-凝聚聚类后完成的数据聚类结果。

如图3(a)-6所示，聚类分析的具体过程如下：

对样本数据进行第一次多维聚类，即进行第一次预聚类-凝聚聚类，分出2个数据聚类，第一次多维聚类结果如图3(a)-3(b)所示，其中，曲线的横坐标为一天内的时刻点，纵坐标为用电负荷(kw)。

第一次多维聚类后，轮廓平均值t＝0.8，不满足t≥(1-m/10)的条件，因此要对第一次多维聚类结果进行第二次多维聚类，即进行第二次预聚类-凝聚聚类，因为只有数据聚类2中样本数量大于2个，因此只需要对数据聚类2进行第二次多维聚类，分出2个数据聚类，第二次多维聚类结果如图4(a)-4(b)所示，其中，曲线的横坐标为一天内的时刻点，纵坐标为用电负荷(kw)。

第二次多维聚类后，轮廓平均值t＝0.7，仍不满足t≥(1-m/10)的条件，因此要对第二次多维聚类的结果继续进行第三次多维聚类，第三次多维聚类结果如图5(a)-5(d)所示，其中，曲线的横坐标为一天内的时刻点，纵坐标为用电负荷(kw)。

第三次多维聚类结束后，轮廓平均值t＝0.7，满足t≥(1-m/10)的条件，最终的5个数据聚类形成，如图6所示，其中，曲线的横坐标为一天内的时刻点，纵坐标为用电负荷(kw)。

步骤s10：根据数据聚类对居民用户进行分类，对居民用户进行分类具体为根据多个预定用电特征指标，获取与多个数据聚类对应的居民用户分类，

预定用电特征指标包括整体负荷水平、用电高峰时段、晚负荷下降时点以及日负荷波动率。

整体负荷水平的负荷水平值的表达式为(13)所示：

plevel代表负荷水平值；paverage为日均负荷；pmax为所有日用电负荷数据的最大值，根据式(13)的计算结果分为高负荷水平(大于等于50％)、较高负荷水平(小于50％且大于等于40％)、中等负荷水平(小于40％且大于等于20％)、低负荷水平(小于20％且大于等于10％)和极低负荷水平(小于10％)共五类。

用电高峰时段包括5点至6点、11点至12点、19点至20点以及20点至21点四个时段。

晚负荷下降时点包括21点和22点两类。

日负荷波动率的表达式为式(14)：

pwave代表日负荷波动率；perror为日负荷的标准差。根据式(14)的计算结果分为有波动(30％及以上)和无波动(30％以下)两类。

居民用户分类包括上班族+小孩综合住户、上班族+老人综合住户、老人家庭住户、单身上班族住户以及综合类多人口住户。

上班族+小孩综合住户：负荷水平值为高负荷水平，用电高峰时段为11点-12点和19点-20点，晚负荷下降时点为21点，日负荷波动率为有波动，在本实施例中，图6中自上至下第二条日用电负荷曲线对应的居民用户的日均用电负荷为204kw，负荷水平值高(40.8％)；存在2个很明显的用电高峰时段，分别在11-12点左右和19-20点左右，并且晚上负荷下降的时点较早，在21点左右，日负荷波动率较大，达33.5％。基于实际调研分析，该类用户符合家中有孩子的居民用户的用电情况，因此将该日用电负荷曲线对应的居民用户分类定义为上班族+小孩综合住户。

上班族+老人综合住户：负荷水平值为中等负荷水平，用电高峰时段为11点-12点和19点-20点，晚负荷下降时点为21点，日负荷波动率为无波动，在本实施例中，图6中自上至下第三条日用电负荷曲线对应的居民用户的用电情况与上班族+小孩综合住户类似，但是日均用电负荷为146kw，整体水平值为中等(29.2％)，低于上班族+小孩综合住户，并且用电负荷很平缓，无明显波动(日负荷波动率小于30％)。基于实际调研分析，该类用户符合老人和上班族的混合式居民用户的用电情况，因此将该日用电负荷曲线对应的居民用户分类定义为上班族+老人综合住户。

老人家庭住户：负荷水平值为低负荷水平，用电高峰时段为5点-6点和20点-21点，晚负荷下降时点为21点，日负荷波动率为无波动，在本实施例中，图6中自上至下第四条日用电负荷曲线对应的居民用户的日均用电负荷为87kw，负荷水平值较低(17.4％)，该类用户存在2个用电高峰，分别在5-6点左右和20-21点左右，晚负荷下降时点在21点附近。基于实际调研分析，该类用户符合老人的生活作息并且节电意识强这一特点。因此将该日用电负荷曲线对应的居民用户分类定义为老人家庭住户。

单身上班族住户：负荷水平值为极低负荷水平，用电高峰时段为20点-21点，晚负荷下降时点为22点，日负荷波动率为无波动，在本实施例中，图6中自上至下第五条日用电负荷曲线对应的居民用户的日均用电负荷仅有44kw，负荷水平值极低(8.8％)，该类用户白天用电负荷相对平缓，用电高峰仅有一个，在20-21点附近，晚负荷下降时点在22点附近。基于实际调研分析，该类用户符合单身上班族住户的用电情况，因此将该日用电负荷曲线对应的居民用户分类定义为单身上班族住户。

综合类多人口住户：负荷水平值为较高负荷水平，用电高峰时段为11点-12点和20点-21点，晚负荷下降时点为22点，日负荷波动率为无波动，在本实施例中，图6中自上至下第一条日用电负荷曲线对应的居民用户的日均用电负荷高达312kw，负荷水平值较高(62.4％)，存在2个很明显的用电高峰时段，分别在11-12点左右和20-21点左右，并且晚上负荷下降的时点较晚，在22点左右，日负荷波动率较小，在30％以下。基于实际调研分析，该类用户符合多人口的综合类住户的用电情况，因此将该日用电负荷曲线对应的居民用户分类定义为综合类多人口住户。

实施例的作用与效果

根据本实施例所涉及的一种基于用电负荷分析的居民用户分类方法，因为首先对日用电负荷数据进行数据预处理获取多个样本数据，接着对样本数据进行预聚类和凝聚聚类获取多个数据聚类，然后通过对多个数据聚类的轮廓平均值与预定的轮廓阈值进行比较判断，然后根据判断结果、凝聚聚类次数以及数据聚类中的样本数据的数量，对样本数据进行重复多次预聚类和凝聚聚类，最后根据数据聚类对居民用户进行分类，所以，本实施例的一种基于用电负荷分析的居民用户分类方法基于贝叶斯准则通过对样本数据进行多次聚类形成多个数据聚类，从而能够快速地进行多个数据聚类的最优化划分，进而根据数据聚类对居民用户进行分类，相较以往的居民用户分类方法，对居民用电负荷的分析更为精细，大大提高对居民用户的分类的准确性，从而让供电单位能够根据居民用户的种类确定各类居民用户的用电负荷特征，进而准确地进行电网系统的供给侧管理，保证电网系统安全稳定运行。

因为本实施例中的数据预处理包括采用牛顿插值法对日用电负荷数据进行数据清洗并进行数据归一化处理，从而获取样本数据，所以使得样本数据分布均匀且可进行不同量纲数据间的整合，从而避免了不同来源的日用电负荷数据造成的数据偏差，保证了多维聚类结果的准确性。

因为本实施例中的轮廓平均值的引入，所以使得多维聚类划分的过程中得到了数学理论的支撑，从而多维聚类划分的过程更为严谨，进而更进一步提高了多维聚类结果的准确性。

因为本实施例中居民用户进行分类具体为根据多个预定用电特征指标，获取对应的与多个数据聚类对应的居民用户分类，又对预定用电特征指标进行分类，所以能够方便供电单位根据用户的用电情况对号入座，合理统筹，从而大大提高了供电单位对电网系统的供给侧的管理和规划能力。

上述实施方式为本发明的优选案例，并不用来限制本发明的保护范围，本领域普通技术人员在所附权利要求范围内不需要创造性劳动就能做出的各种变形或修改仍属本专利的保护范围。