单轴荷载下的岩石块度分形损伤演化本构模型建立方法与流程

本发明属于岩石力学研究技术领域，具体涉及一种单轴荷载下的岩石块度分形损伤演化本构模型建立方法。

背景技术：

岩石是一种非均质的地质材料，内含大量随机分布的孔隙、空洞、界面等缺陷，这种材料在载荷作用下，其内部结构的力学性质将持续发生变化，研究岩石本构关系问题一直是岩石力学研究的重点之一，在工程爆破、矿山开采、矿石粉碎、隧道开挖、覆岩稳定性计算等许多领域的工程实践中都有着广泛应用。

一方面，现有技术中，学者们从岩石材料内部所含缺陷分布的随机性出发，将连续损伤理论和统计强度理论有机地结合起来，从岩石微元强度服从正态分布或weibull分布的角度出发，使岩石本构模型的研究取得了重大进展，但是，现有岩石本构模型比较多，但往往都难以反映实际。

另一方面，大量的研究以及工程施工实践证明：岩石的宏观破碎是由岩体内大量的原生裂隙、孔隙以及如温度、含水率、受荷情况等外部环境的多种因素相互作用共同影响的结果，且岩石宏观破裂的形成并不是一次性造成，而是由加载过程中多处小破裂演化扩展相互交联积聚的结果，该过程虽然是随机的但仍然具有统计自相似性，因此岩石破坏后的碎块也具有分形特征，即块度分形；由于岩石破碎后的碎块分布是其损伤破坏结果的体现。因此块度分形维数可以用来定量描述岩石的破碎效果和表征岩石内部的损伤演化情况，所以运用分形理论来解决岩石破坏损伤规律是可行的；但是，现有技术中还缺乏运用分形理论来进行岩石破坏损伤规律的研究，这方面的研究工作还有待于系统和深化。

技术实现要素：

本发明所要解决的技术问题在于针对上述现有技术中的不足，提供一种单轴荷载下的岩石块度分形损伤演化本构模型建立方法，其方法步骤简单，实现方便，建立起了采用岩石块度分形维数来表征岩石内部的损伤演化情况的模型，能够较为真实地反映实际，实用性强，推广应用价值高。

为解决上述技术问题，本发明采用的技术方案是：一种单轴荷载下的岩石块度分形损伤演化本构模型建立方法，该方法包括以下步骤：

步骤一、基于weibull分布建立岩石损伤演化本构关系式，具体过程为：

步骤101、假设岩石强度值的概率密度符合weibull分布，将其概率密度函数p(ε)表示为：

其中，ε为岩石应变，m和f为用于表示岩石的力学特性的weibull分布的参数；

步骤102、假设岩石内部微单元的总个数为n,在外力作用下已发生破坏的微单元个数为nt，将损伤变量d表示为：

d＝nt/n(f2)

步骤103、将当岩石应变ε增加时在外力作用下已发生破坏的微单元个数nt表示为：

步骤104、将公式(f3)代入公式(f2)，得到：

步骤105、建立岩石损伤演化本构关系式为：

σ＝eε(1-δd)(f5)

其中，e为弹性模量，δ为岩石损伤比例系数；

步骤二、建立基于块度分形维数的岩石块度分形损伤演化本构关系式：结合分形维数与岩石损伤的关系，用块度分形维数约化处理后的块度分形系数f替换公式(f5)中的岩石损伤比例系数δ，得到基于块度分形维数的岩石块度分形损伤演化本构关系式为：

σ＝eε(1-fd)(f6)

步骤三、建立单轴荷载下的岩石块度分形损伤演化本构模型，具体过程为：

步骤301、将公式(f4)代入公式(f6)，得到岩石块度分形损伤演化本构模型为：

步骤302、确定出单轴荷载下用于表示岩石的力学特性的weibull分布的参数m和f；

步骤303、将步骤302中确定出的参数m和f代入公式(f7)，建立出单轴荷载下的岩石块度分形损伤演化本构模型。

上述的单轴荷载下的岩石块度分形损伤演化本构模型建立方法，步骤二中所述块度分形系数f的确定方法为：其中，d为块度分形维数值，dmax为同尺度下最大块度分形维数值。

上述的单轴荷载下的岩石块度分形损伤演化本构模型建立方法，步骤302中所述确定出单轴荷载下用于表示岩石的力学特性的weibull分布的参数m和f的具体方法为：

步骤3021、设岩石应力-应变曲线的峰值强度点为(εc，σc)；

步骤3022、令岩石应力-应变曲线的峰值强度点(εc，σc)处的导数为0，得到公式：

步骤3023、在峰值强度点(εc，σc)处满足关系式：

步骤3024、联立公式(f8)和公式(f9)，解得参数m和f分别为：

上述的单轴荷载下的岩石块度分形损伤演化本构模型建立方法，步骤303中将步骤302中确定出的参数m和f代入公式(f7)，建立出的单轴荷载下的岩石块度分形损伤演化本构模型为：

本发明与现有技术相比具有以下优点：

1、本发明的方法步骤简单，实现方便，通过建立单轴荷载下的岩石块度分形损伤演化本构模型，建立起了采用岩石块度分形维数来表征岩石内部的损伤演化情况的模型，为岩体的块度预测提供了一种简便、快捷、易操作的方法，应用到工程实际中进行岩体的块度预测，能够有效地节省人力成本和时间。

2、本发明采用块度分形系数代替了传统的损伤系数，建立了一个新的描述岩石损伤过程的本构方程，即单轴荷载下的岩石块度分形损伤演化本构模型，建立起了采用岩石块度分形维数来表征岩石内部的损伤演化情况的模型，有助于运用分形理论来进行岩石破坏损伤规律的研究的系统和深化，而且，经过实验验证，采用该模型计算得到的理论应力-应变曲线与实验应力-应变曲线误差较小，能够较为真实地反映实际。

3、本发明的方法能够推广应用到工程爆破、矿山开采、矿石粉碎、隧道开挖、覆岩稳定性计算等许多领域的工程实践中，能够为采矿、隧道等地下工程空间破碎围岩的破碎程度预测提供方法，为采取合理的支护措施和方法设计提供科学参考依据，该方法可解决采用常规测量方法无法测量围岩破碎程度的难题；实用性强，推广应用价值高。

综上所述，本发明的方法步骤简单，实现方便，建立起了采用岩石块度分形维数来表征岩石内部的损伤演化情况的模型，能够较为真实地反映实际，实用性强，推广应用价值高。

下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。

附图说明

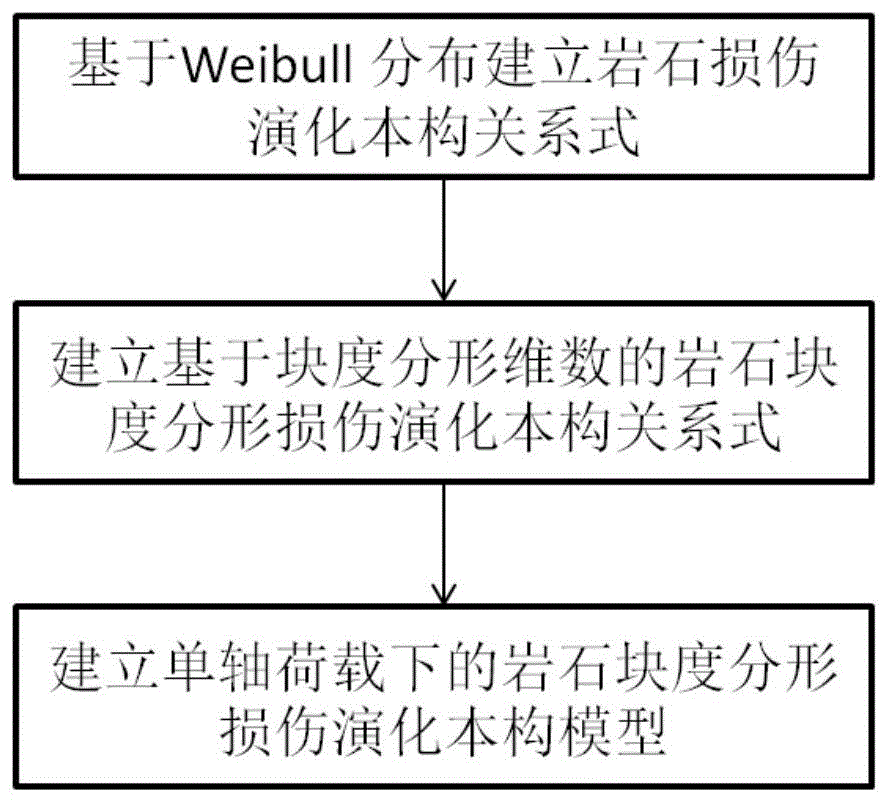
图1为本发明的方法流程框图。

图2a为加载速率为0.001mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图。

图2b为加载速率为0.005mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图。

图2c为加载速率为0.01mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图。

图2d为加载速率为0.05mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图。

具体实施方式

如图1所示，本发明的单轴荷载下的岩石块度分形损伤演化本构模型建立方法，该方法包括以下步骤：

步骤一、基于weibull分布建立岩石损伤演化本构关系式，具体过程为：

步骤101、假设岩石强度值的概率密度符合weibull分布，将其概率密度函数p(ε)表示为：

其中，ε为岩石应变，m和f为用于表示岩石的力学特性的weibull分布的参数；

步骤102、假设岩石内部微单元的总个数为n,在外力作用下已发生破坏的微单元个数为nt，将损伤变量d表示为：

d＝nt/n(f2)

步骤103、将当岩石应变ε增加时在外力作用下已发生破坏的微单元个数nt表示为：

步骤104、将公式(f3)代入公式(f2)，得到：

步骤105、建立岩石损伤演化本构关系式为：

σ＝eε(1-δd)(f5)

其中，e为弹性模量，δ为岩石损伤比例系数；

步骤二、建立基于块度分形维数的岩石块度分形损伤演化本构关系式：结合分形维数与岩石损伤的关系，用块度分形维数约化处理后的块度分形系数f替换公式(f5)中的岩石损伤比例系数δ，得到基于块度分形维数的岩石块度分形损伤演化本构关系式为：

σ＝eε(1-fd)(f6)

本实施例中，步骤二中所述块度分形系数f的确定方法为：其中，d为块度分形维数值，dmax为同尺度下最大块度分形维数值。

具体实施时，对多个同尺度的岩石试块进行单轴荷载下的破碎实验并求取块度分形维数值，dmax即为同尺度下的最大块度分形维数值。求取块度分形维数值的方法可以采用现有技术中对岩石块度分形维数预测的方法，如(1)利用裂隙分形维数与块度分形维数有着相同的分形意义，建立二者之间的联系，通过裂隙分形维数预测块度；(2)直接的几何拓扑计算方法；(3)断裂能量耗散方法。

步骤三、建立单轴荷载下的岩石块度分形损伤演化本构模型，具体过程为：

步骤301、将公式(f4)代入公式(f6)，得到岩石块度分形损伤演化本构模型为：

步骤302、确定出单轴荷载下用于表示岩石的力学特性的weibull分布的参数m和f；

本实施例中，步骤302中所述确定出单轴荷载下用于表示岩石的力学特性的weibull分布的参数m和f的具体方法为：

步骤3021、设岩石应力-应变曲线的峰值强度点为(εc，σc)；

步骤3022、令岩石应力-应变曲线的峰值强度点(εc，σc)处的导数为0，得到公式：

步骤3023、在峰值强度点(εc，σc)处满足关系式：

步骤3024、联立公式(f8)和公式(f9)，解得参数m和f分别为：

步骤303、将步骤302中确定出的参数m和f代入公式(f7)，建立出单轴荷载下的岩石块度分形损伤演化本构模型。

本实施例中，步骤303中将步骤302中确定出的参数m和f代入公式(f7)，建立出的单轴荷载下的岩石块度分形损伤演化本构模型为：

为了验证本发明的方法建立的单轴荷载下的岩石块度分形损伤演化本构模型的准确性与适用性，将不同加载速率下，根据公式(f10)和公式(f11)分别计算得到的参数m和f代入公式(f12)中，得到基于岩石块度分形损伤演化本构方程计算得到的应力-应变关系曲线，即岩样的块度分形损伤演化本构方程的理论模型，并与实验的应力-应变关系曲线进行对比。其中，各个加载速率与块度分形系数f、参数m和f的对应关系表如表1所示，加载速率为0.001mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图如图2a所示，加载速率为0.005mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图如图2b所示，加载速率为0.01mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图如图2c所示，加载速率为0.05mm/s时的理论模型应力-应变关系曲线和实验应力-应变关系曲线对比图如图2d所示。

表1各个加载速率与f、m和f的对应关系表

从图2a、2b、2c和2d能够看出，虽然存在一定误差，但在峰值强度前，试验曲线与模型曲线拟合度相对较好，该模型能够较好的反映岩石峰前破裂过程中应力应变的总体趋势；模型曲线的峰后情况与试验曲线有较大误差，这是主要由于弹性模量取值的问题造成的，但对于本申请研究的损伤强度点是峰值应力点，其误差还在可接受范围之内；且由图可知加载速率越大，模型曲线和实验曲线的拟合误差越小；由于该模型未考虑岩石在加载过程中孔隙裂隙的闭合情况，所以峰值强度前模型曲线未出现下凹，因此如果不考虑岩石压缩阶段的非线性变形,模型曲线和试验曲线的误差会更小。

以上所述，仅是本发明的较佳实施例，并非对本发明作任何限制，凡是根据本发明技术实质对以上实施例所作的任何简单修改、变更以及等效结构变化，均仍属于本发明技术方案的保护范围内。