一种振动信号去噪的模态混叠消除方法与流程

本发明涉及振动信号领域，具体涉及一种用于振动信号去噪的方法。

背景技术：

在现场的爆破测振过程中，由于测振仪器受到外界及自身因素的干扰，测得的信号中往往存在噪声，从而对振动信号的分析产生影响，故需要对信号进行时频分析以去除噪音的影响。目前常用的信号去噪方法有fourier变换、小波变换、希尔伯特-黄变换hht(hilbert-huangtransform)等。其中，fourier变换是处理信号噪音最传统的方法，但fourier变换只能在频域内进行分析，若信号在时域上某处发生突变，则会对整个频域产生影响，无法分辨信号的尖峰是突变还是噪音导致。因此在20世纪80年代出现了小波变换理论，小波变换能对信号在时域和频域内进行转换，进而达到较好的去噪效果。但小波变换分解的精度依赖小波基的选择，而选择小波基本身就具有一定的模糊性，且小波基的长度有限，会造成信号能量的泄露等，而hht变换(由希尔伯特变换hilbert和经验模态分解emd组成)可以直接将原始信号按不同的时间尺度进行emd分解，分解成一系列从高频到低频的imf分量，能很好地提取非平稳信号变化的特征；与小波变换相比，hht不需要选择基函数，且具有自适应性和多分辨率的特点，可以更好地对非平稳信号进行时频分析，但在实际滤波的去噪过程中，发现hht也存在一些问题，由李夕兵等主编的2009年由北京科学出版社出版的《爆破振动信号分析理论与技术》一书中的第100-105页，提到了imf分量的正交性问题，该方法存在不完全正交的缺点，即emd分解出的imf分量之间会出现模态混叠现象；曹莹等于2016年在电机与控制学报上发表的《多尺度形态滤波模态混叠抑制方法》也提到了模态混叠现象，即分解出的imf分量不满足频率的依次递减性和主频的唯一性，对之后的hht滤波去噪效果会产生影响，并采用多尺度形态滤波的方法抑制了一定程度上的混叠现象。

技术实现要素：

目前针对imf分量混叠问题，在此引入主成分分析(pca)，采用pca对emd进行了改进，提出了pemd滤波降噪法，将原始信号通过emd分解出的imf分量组合转换为正交的主成分分量组合，继而通过主成分分量的重构生成正交的原始信号，达到emd完全正交分解信号的目的，以便更好地进行后续滤波去噪处理。

本发明的技术方案为：一种振动信号去噪的模态混叠消除方法，它包括以下步骤：

⑴提取原始数据；

⑵对原始数据进行标准化处理；

⑶计算相关系数矩阵；

⑷计算相关系数的特征值和特征向量；

⑸计算特征值的累计贡献率；

⑹构建由特征向量组成的正交主成分分量；

⑺选择累计贡献率达到95％以上的特征值组合，得到相对应的主成分分量组合，再分别以各个主成分的贡献率为权重，构建主成分综合评价的信号模型，生成新的正交原始信号；

⑻对新的正交原始信号进行emd分解，得到完全正交的imf分量，消除各分量之间的模态混叠效应，进而将具有不同特征的振动信号和噪音分离到不同的imf分量中；

⑼根据现场测振的实际情况，滤除噪音所在的imf分量，再进行信号重构，以达到滤波去噪效果。

优选的，所述的提取原始数据，具体是将原始信号x(t)通过emd分解成m个imf指标，每个分量都取n个采样点。

优选的，所述的原始数据标准化处理，具体计算公式如下：

假设进行主成分分析的指标变量imf分别为x1,x2,…,xm，第i个采样点的第j个imf分量的取值为aij，将aij转换成标准化值有

式中：μj为j个指标变量imf均值；sj为第j个指标变量imf标准差。

同时，将指标变量进行标准化处理，即

式中：为标准化的imf。

优选的，所述的计算相关系数矩阵r，具体计算公式如下：

^r＝(rij)m×m

优选的，所述的计算特征值和特征向量，具体计算公式如下：

计算相关系数矩阵r的特征值λj，得到对应的特征向量uj＝[u1j,u2j,…,umj]^t,j＝1,2，…,m。

优选的，所述的计算特征值的累计贡献率，具体计算公式如下：

式中：bj为第j个特征值的信息贡献率，αp为前p个特征值的累计贡献率。

优选的，所述的构建由特征向量组成的主成分分量，具体计算公式如下：

由特征向量组成的m个新主成分分量yj为

优选的，所述的选择累计贡献率达到95％以上的主成分分量组合，由于各主成分分量之间完全正交，故可分别以各个主成分的贡献率为权重，构建主成分综合评价的信号模型，重构生成新的正交原始信号。

优选的，所示的对新的正交原始信号进行emd分解，得到完全正交的imf分量，消除了各分量之间的模态混叠效应，进而将具有不同特征的振动信号和噪音分离到不同的imf分量中。

优选的，所述的对所得的正交imf分量进行滤波处理，再进行信号重构。

有益效果为：由于pemd是从信号本身的特性出发，将信号完全正交分解，具有不同特征的振动信号和噪音被分离到不同的imf分量中，通过与经典emd算法和eemd改进算法对比，得到pemd算法在仿真模拟实验信号和实测爆破振动信号的去除模态混叠效果及去噪效果上均优于eemd和emd，达到了最佳的效果。

附图说明

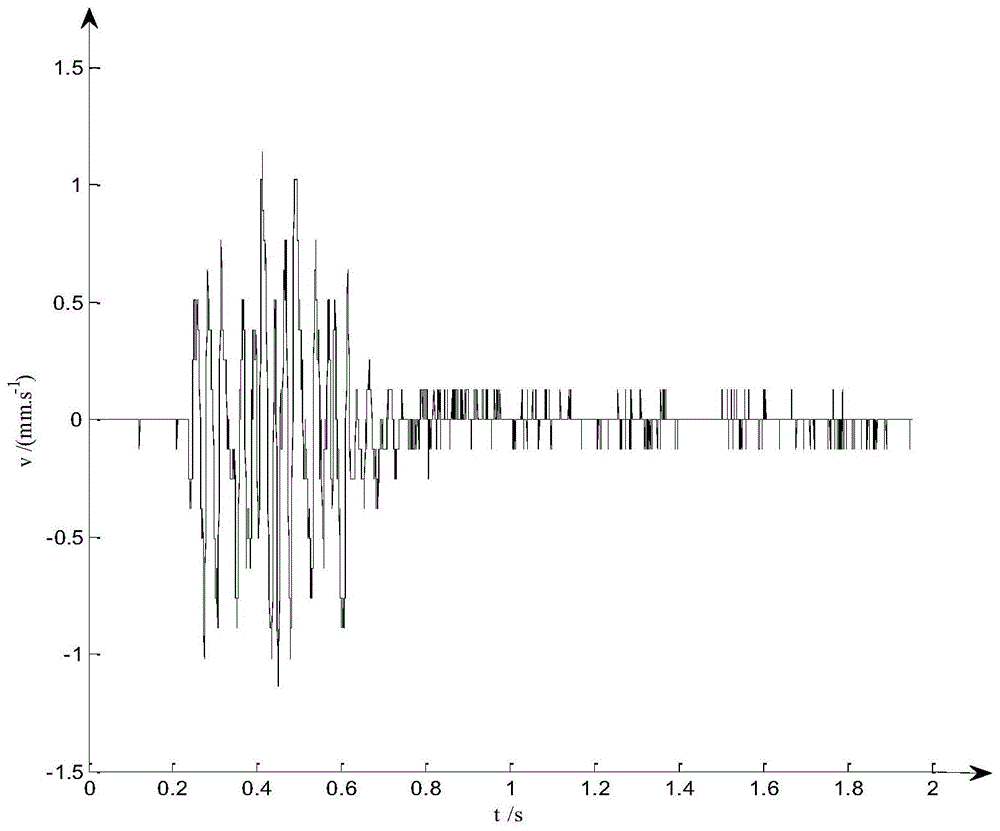
图1是本发明所涉及的爆破振动信号速度时程曲线图；

图2是本发明所涉及的爆破振动信号imf分量图；

图3是本发明所涉及的爆破振动信号特征向量表；

图4是本发明所涉及的爆破振动信号主成分分量的累计贡献率图；

图5是本发明所涉及的爆破振动信号重构对比图；

图6是本发明所涉及的爆破振动信号模态混叠消除对比图；

图7是本发明所涉及的爆破振动信号去噪效果对比图；

图8是本发明所涉及的爆破振动信号去噪能量对比图。

具体实施方式

针对江西省铅山县永平露天铜矿爆破测振描述了本发明的原理以及具体实施方式，试验地点选在江西省铅山县永平露天铜矿，测点布置在东部边坡台阶上，爆破振动测试采用加拿大instantel公司生产的blastmateiii型测振仪，本次测试信号的采样率为2048hz，故其奈奎斯特(nyquist)频率为1024hz，对所测得的一组原始数据取前4000个采样点，如图1所示。采用本发明的振动信号去噪的模态混叠消除方法进行去噪处理，具体步骤如下：

⑴将爆破振动信号s(t)通过emd分解成11个固有模态函数(imf)指标分量c1～c11，如图2所示；

⑵对原始数据进行标准化处理。进行主成分分析的指标变量imf分别为x1,x2,…,x11，第i个采样点的第j个imf的值为aij，将aij转换成标准化值有

式中：μj为第j个imf的均值；sj为第j个imf的标准差；

同时，将指标变量imf进行标准化处理，即

式中：为标准化的imf；

⑶计算相关系数矩阵r。

r＝(rij)11×11

式中r为相关系数矩阵；

⑷计算特征值与特征向量

计算相关系数矩阵r的特征值λj，得到对应的特征向量uj＝[u1j,u2j,…,u11j]^t,j＝1,2，…,11，如图3，其中行项代表标准化的imf分量列项代表相关系数矩阵特征值对应的特征向量uj；

⑸计算前p个特征值的累计贡献率。

式中：bj为第j个特征值的信息贡献率，αp为前p个特征值的累计贡献率；计算可得，前10个特征值的累计贡献率达到了96％，故取p＝10，如图4；

⑹构建主成分分量由前10个特征值所对应的特征向量uj组成的10个新主成分分量yj为

⑺重构爆破振动信号

选择前10个主成分分量进行信号重构，生成新的正交原始信号，拟合的剩余标准差rmse为0.0033，如图5；

⑻去除模态混叠

对新的正交原始信号进行emd分解，得到完全正交的imf分量，消除了各分量之间的模态混叠效应，进而将具有不同特征的振动信号和噪音分离到不同的imf分量中。通过与原始数据emd分解和eemd分解的对比，取前六个模态混叠现象较为明显的imf分量c1～c6进行分析，得到去除模态混叠的效果如图7所示。

由图6可知，三者的c1均为噪音，频率范围均分布在0～1000hz，emd分解的c2与c3的频带分别在0～80hz和0～150hz之内，不符合依次递减的规律，c4与c5的频带均在0～100hz，且c5具有多种主频。c6在0～30hz的范围具有多种主频，不具备唯一性，故直接使用emd分解出的imf分量均发生了混叠效应。eemd分解的分量频谱以此处于0～1000、0～600、0～200、0～150、0～50、0～30hz的范围，除了c5与c6，其余分量基本上符合依次递减的规律，在一定程度上减轻了混叠现象；但是从主频上来看，c2、c3以及c6的主频不唯一。而pemd分解的imf分量，其频率分布范围依次在0～1000、0～120、0～100、0～80、0～50、0～30hz，符合分解之后频率依次递减的规律，且各分量主频也均符合唯一性，故对比之下，改进算法pemd的去混叠效果最佳。且pemd分解结果稳定不变，具有唯一性；

⑼滤波去噪

根据现场测振的实际情况，滤除噪音所在的imf分量，再进行信号重构，以达到滤波去噪效果，如图7所示。

从图7左侧时域信号可以看出，emd和eemd滤波去噪方法可以滤掉部分噪声，但是相比pemd，去噪之后的信号中仍有很的噪声成分。而采用pemd滤波去噪方法得到的信号更为光滑，去掉的噪声信号相对更多，因此去噪效果最好。从图7右侧频谱分析，爆破振动信号主频带分布在0～130hz，根据张声辉等于2019年在振动与冲击期刊上发表的《露天边坡爆破地震波能量分布特征研究》可知，永平铜矿爆破振动信号的主频带分布在0～64hz，故该爆破振动信号受到了高频噪音的污染，通过emd和eemd滤波去噪后的信号主频均分布在0～95hz，压制了部分高频噪音；而pemd滤波去噪信号主频分布在0～64hz的范围内，很好的滤掉了绝大部分高频噪音。故无论从时域还是频域分析，pemd滤波效果均优于eemd和emd；

从能量的角度对三者的滤波去噪效果进行分析，如图8所示。

由图8中的柱状能量图可知，原始信号s(t)从低频到高频能量呈现先减后增的趋势，是由于原始信号含有低频的振动信号和较多的高频噪音，而经过emd、eemd和pemd滤波后的信号，能量从低频到高频呈现依次减少的趋势，是因为这三种方法均滤掉了部分高频噪音能量，留下了中低频的信号能量。

由图8中的振动信号-噪音折线能量占比图可知，emd、eemd和pemd的振动信号能量百分比均逐渐提高，噪音能量所占比例逐渐下降，故经过滤波后三者均达到了去噪效果，且pemd的振动信号能量所占比例达到了98.2％以上，噪音只占1.8％左右，很好地去除了绝大部分噪音能量。故从能量角度分析，pemd去噪效果最优。

以上所述仅为本发明的实施例，并非因此限制本发明的专利范围，凡是利用本发明说明书及附图内容所作的等效流程变换，或直接或间接运用在其他相关的技术领域，均同理包括在本发明的专利保护范围内。