自然破片战斗部破片质量与数量分布预测仿真计算方法与流程

本发明涉及破片战斗部威力仿真领域，特别涉及一种自然破片战斗部破片质量与数量分布预测仿真计算方法。

背景技术：

破片质量与数量分布是设计具有理想破片杀伤效应弹丸的重要问题，而影响破片质量、数量分布的因素很多，其中包括一些随机因素，这就导致要想对这些因素进行理论分析很难。在弹丸设计过程中，为了选择具有最佳破片杀伤效应的设计方案，需在几个不同方案，如不同结构、或不同弹体材料、或不同炸药中进行筛选。在方案筛选中，都是用实际战斗部的破碎性试验求得破片质量与数量分布数据，不仅耗费大量的人力、物力、财力，而且研制周期较长。

为了解决上述问题，科研人员力图在研制过程中，至少是方案筛选时，避免进行实际战斗部的破碎性试验，而是通过理论分析或简单实验来解决问题。目前，广泛用于预测自然破片质量、数量分布的有mott实验公式，但该公式存在大、小破片区偏离实验值较大的问题，而且对于给定的条件，必须用实验测定破碎参数，而这并不容易；sternberg为了弥补mott公式的不足，提出了按质量将破片分为三个区域，并给出了三个不同实验公式，该公式虽然避免了大、小破片区偏离实验值的问题，但待定常数多，使用不便；松永美之公式与特定的试验结果比较吻合，但该分布公式没有考虑弹体材料对破碎性的影响；其它一些破片质量分布式，如矶部公式、铃木公式等，也都忽略了材料的影响。

技术实现要素：

鉴于上述问题，本发明的目的在于提供一种在自然破片战斗部设计过程中，仅需通过简单模拟试验测出单位长度修正payman参数cu和c/m比值关系，即能较为准确预测自然破片战斗部的破片质量与数量分布，以完成各种战斗部设计方案筛选工作的高效的预测仿真计算方法。

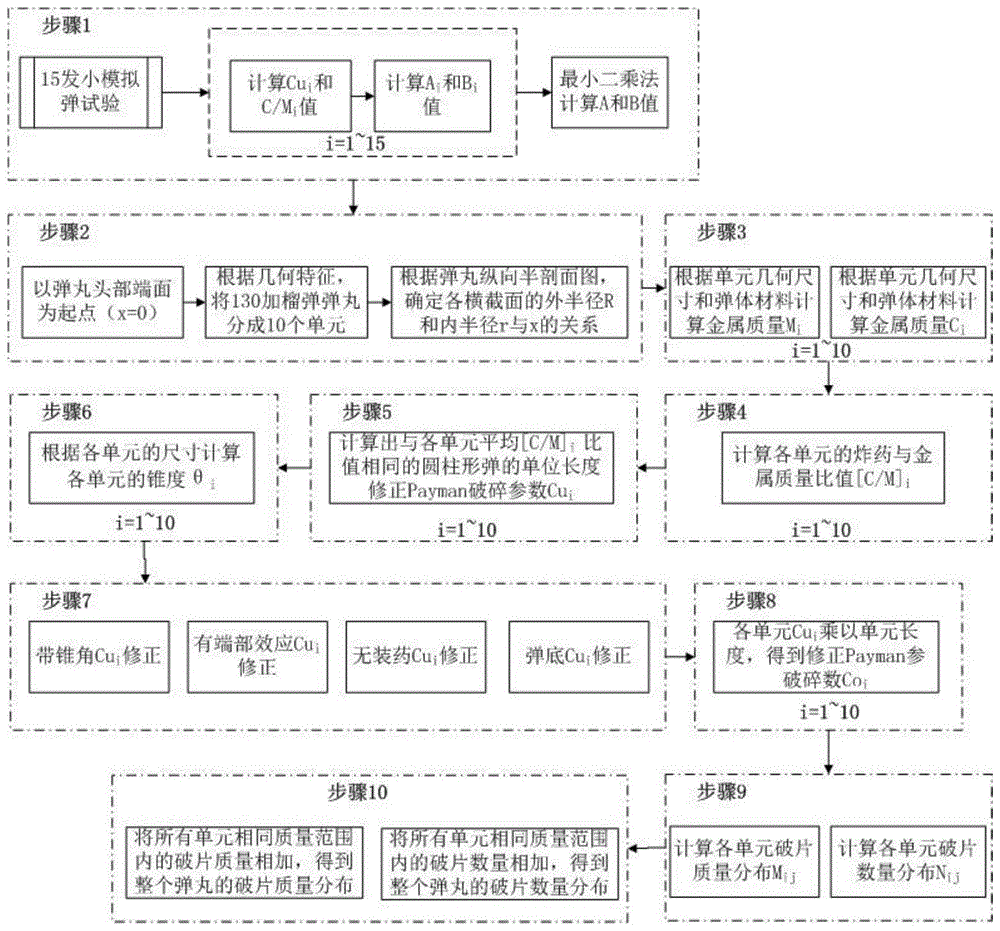
为了实现上述目的，本发明的技术方案为：一种自然破片战斗部破片质量与数量分布预测仿真计算方法，其特征在于：包括以下步骤：

步骤1、采用与战斗部具有相同材料、相同热处理工艺、相同炸药含量的小圆柱形模拟弹进行静爆试验，计算单位长度修正payman破碎参数cu，利用在给定材料、热处理工艺、炸药含量情形下cu与c/m的线性关系，计算出弹体材料与炸药组合的特征常数a、b值；

步骤2、根据战斗部纵向半剖图按几何特征将战斗部划分成n个单元；

步骤3、根据单元的几何尺寸和弹体材料与炸药的密度，计算各单元的金属质量mi和炸药质量ci，其中，i取值为0-n；

步骤4、计算各单元的炸药质量ci与金属质量mi的比值

步骤5、将各单元的值代入已知的cu＝a+b×(c/m)中，计算出各单元的单位长度修正payman破碎参数cui；

步骤6、根据各单元的几何尺寸计算各单元的锥角；

步骤7、根据各单元的几何特征，分别对各单元的单位长度修正payman破碎参数进行修正，得到修正后的cui’；

步骤8、各个单元的cui’值乘以各自单元的长度，得到各单元的修正payman破碎参数coi；

步骤9、计算各个单元的破片质量与数量分布；

步骤10、将所有单元的相同质量范围内的破片质量和数量相加，得到整个战斗部的破片质量与数量分布。

进一步的，所述步骤1中采用与战斗部具有相同材料、相同热处理工艺、相同炸药含量的小圆柱形模拟弹进行静爆试验，计算单位长度修正payman破碎参数cu，具体包括：

步骤1-1、根据破片积累质量百分数p的对数与无量纲破片质量m/mr之间的线性关系[1]计算修正payman破碎参数co，公式为

式中m为破片质量；mr为回收破片的总质量，当回收率很高时近似等于弹体的金属质量m；m/mr称为无量纲破片质量，p为质量大于m的破片积累质量百分数；

步骤1-2、根据修正payman破碎参数co与弹体长度l间的正比关系[2]计算单位长度修正payman破碎参数，即：

其中,比例系数cu为单位长度修正payman破碎参数。

进一步的，所述步骤1中利用在给定材料、热处理工艺、炸药含量情形下cu与c/m的线性关系，计算出弹体材料与炸药组合的特征常数a、b值，具体为：

对于给定的弹体材料和炸药，单位长度修正payman破碎参数cu与c/m间存在如下公式[3]，即

其中，c为炸药质量，m为弹体的金属质量，a和b是弹体材料与炸药组合的特性常数；

以步骤1中小圆柱形模拟弹试验数据为依据，取得每发模拟弹的c/m比值，用xi表示，及单位长度修正payman破碎参数cui，用yi表示，得到关系[3]的线性拟合关系为如下公式[4]，即

yi＝a+bxi+εi(i＝1,2,…,n)[4]

其中,(xi，yi)表示(c/m，cu)的第i个样本观察值，利用最小二乘法原理，计算取值最小时的a、b值。

进一步的，所述步骤7中根据各单元的几何特征，分别对各单元的单位长度修正payman破碎参数进行修正，得到修正后的cui’，具体为：

步骤7-1、对于相同材料和炸药组合，平均c/m比值相同的带锥度弹和圆柱弹之间存在如下公式

cu(带锥度弹)＝(1-t1θ)cu(圆柱弹)[5]

其中，t1为锥度修正系数，θ为表面锥度，当内表面和外表面都带锥度时取其平均值，即带锥度弹按公式[5]得到修正的cui’；

步骤7-2、对于存在起爆端端部效应的情况，端部效应导致破碎性降低，对比相应无端部效应的弹，存在如下公式

cu(有端部效应)＝cu(无端部效应)-t2a[6]

其中，t2为端部效应修正系数，常数a与公式[3]中一致，即对于存在有端部效应的按公式[6]式得到修正的cui’；

步骤7-3、对于无装药的空弹体情形，无装药部分的修正payman破碎参数co按如下公式[7]估算，

co(无装药部分)＝t3a[7]

其中，t3为无装药修正系数，常数a与公式[3]中一致，即对于无装药部分的按公式[7]式得到修正的co’，并基于公式[2]得到修正的cui’；

步骤7-4、对于存在弹底的情形，分邻近圆柱部分、底这两部分考虑，则存在如下公式[8]和[9]，

cu(底)＝t5cu(邻近圆柱部分)[9]

其中，t4t5为弹底修正系数，t4取值0-1之间，t5取值0-1之间，即对于存在弹底情形按公式[8]、[9]得到修正的cui’。

进一步，所述步骤9具体包括：

步骤9-1、依据国军标相关标准规范确定不同破片质量mi(i＝1,2,...,k)系列阈值；

步骤9-2、依据公式[1]得到破片质量在mi到mj范围内的破片总质量为：

其中，mij为质量在mi到mj范围内的破片总质量；mi和mj为破片质量分组的下限和上限，mj>mi；m为战斗部各单元的弹体金属质量总和，即弹体的金属质量；α为质量修正系数，其值根据模拟试验数据选取；

步骤9-3、各质量范围内的破片数量为：

其中，a和b是加权系数，a+b＝1，其值根据模拟试验数据选取。

与现有技术相比，本发明的优点在于：

首先，本方法以破碎性相似关系为基础，简便易行，实用性强，只需要通过少量小圆柱形弹模拟试验即可测出弹体材料与炸药组合的特性常数a和b，利用战斗部纵向半剖图就能计算任意战斗部的破片质量与数量分布；

其次，通过几何因素的修正，特别是弹底和无装药部分的修正以及质量修正系数α和加权系数a与b的引入，大大提高了预测结果的精度；

最后，这种方法既考虑了炸药和弹体结构的影响，也考虑了弹体材料的影响，在战斗部设计中可应用此方法进行弹形选择、炸药选择、弹体材料及其热处理工艺选择，实现弹体材料、炸药和结构的合理匹配，设计出具有理想破片杀伤效应的战斗部。

附图说明

图1为本发明的自然破片战斗部破片质量与数量分布预测仿真计算流程示意图。

图2为根据130加榴弹弹丸的纵向半剖图将弹丸分为10个单元结构示意图。

图3为弹丸破片质量与数量分布预测计算软件之计算指标导入示意图，包括弹体密度、炸药密度、ab值、弹体单元内外径等计算指标。

图4为弹丸破片质量与数量分布预测计算软件之破片质量与数量分布计算示意图。

图5为弹丸破片质量与数量分布预测计算软件之预测结果汇总表示意图。

图6为弹丸破片质量与数量分布预测计算软件之破片质量分布预测结果示意图。

图7为弹丸破片质量与数量分布预测计算软件之破片数量分布预测结果示意图。

图8为弹丸破片质量与数量分布预测计算软件之各单元参数结果预测结果示意图。

具体实施方式

如图1-8所示公开了本申请自然破片战斗部破片质量与数量分布预测仿真计算方法的流程及相关结果。

该方法具体包括：

步骤1、采用与战斗部具有相同材料、相同热处理工艺、相同炸药含量的小圆柱形模拟弹进行静爆试验，计算单位长度修正payman破碎参数cu，利用在给定材料、热处理工艺、炸药含量情形下cu与c/m的线性关系，计算出弹体材料与炸药组合的特征常数a、b值；

其中，计算单位长度修正payman破碎参数cu，具体包括：

步骤1-1、根据破片积累质量百分数p的对数与无量纲破片质量m/mr之间的线性关系[1]计算修正payman破碎参数co，公式为

式中m为破片质量；mr为回收破片的总质量，当回收率很高时近似等于弹体的金属质量m；m/mr称为无量纲破片质量，p为质量大于m的破片积累质量百分数；

步骤1-2、根据修正payman破碎参数co与弹体长度l间的正比关系[2]计算单位长度修正payman破碎参数，即：

其中,比例系数cu为单位长度修正payman破碎参数。

而计算出弹体材料与炸药组合的特征常数a、b值，则具体为：

对于给定的弹体材料和炸药，单位长度修正payman破碎参数cu与c/m间存在如下公式[3]，即

其中，c为炸药质量，m为弹体的金属质量，a和b是弹体材料与炸药组合的特性常数；

为了获取最能反映出cu与c/m之间的线性关系，以步骤1中小圆柱形模拟弹试验数据为依据，取得每发模拟弹的c/m比值，用xi表示，及单位长度修正payman破碎参数cui，用yi表示，得到关系[3]的线性拟合关系为如下公式[4]，即

yi＝a+bxi+εi(i＝1,2,…,n)[4]

其中,(xi，yi)表示(c/m，cu)的第i个样本观察值，利用最小二乘法原理，计算取值最小时的a、b值，换言之，此a、b值即为所求。

步骤2、根据战斗部纵向半剖图按几何特征将战斗部划分成n个单元；

步骤3、根据单元的几何尺寸和弹体材料与炸药的密度，计算各单元的金属质量mi和炸药质量ci，其中，i取值为0-n；

步骤4、计算各单元的炸药质量ci与金属质量mi的比值

步骤5、将各单元的值代入已知的cu＝a+b×(c/m)中，计算出各单元的单位长度修正payman破碎参数cui；

步骤6、根据各单元的几何尺寸计算各单元的锥角；

步骤7、根据各单元的几何特征，分别对各单元的单位长度修正payman破碎参数进行修正，得到修正后的cui’；

由于弹的各单元的几何特征不一，故而需分情况有针对性的进行修正，具体而言：

步骤7-1、对于相同材料和炸药组合，平均c/m比值相同的带锥度弹和圆柱弹之间存在如下公式

cu(带锥度弹)＝(1-t1θ)cu(圆柱弹)[5]

其中，t1为锥度修正系数，θ为表面锥度，当内表面和外表面都带锥度时取其平均值，即带锥度弹按公式[5]得到修正的cui’；

步骤7-2、对于存在起爆端端部效应的情况，端部效应导致破碎性降低，对比相应无端部效应的弹，存在如下公式

cu(有端部效应)＝cu(无端部效应)-t2a[6]

其中，t2为端部效应修正系数，常数a与公式[3]中一致，即对于存在有端部效应的按公式[6]式得到修正的cui’；

步骤7-3、对于无装药的空弹体情形，无装药部分的修正payman破碎参数co按如下公式[7]估算，

co(无装药部分)＝t3a[7]

其中，t3为无装药修正系数，常数a与公式[3]中一致，即对于无装药部分的按公式[7]式得到修正的co’，并基于公式[2]得到修正的cui’；

步骤7-4、对于存在弹底的情形，分邻近圆柱部分、底这两部分考虑，则存在如下公式[8]和[9]，

cu(底)＝t5cu(邻近圆柱部分)[9]

其中，t4t5为弹底修正系数，t4取值0-1之间，t5取值0-1之间，即对于存在弹底情形按公式[8]、[9]得到修正的cui’；

步骤8、各个单元的cui’值乘以各自单元的长度，得到各单元的修正payman破碎参数coi；

步骤9、计算各个单元的破片质量与数量分布；在该步骤中，具体对应有，

步骤9-1、依据国军标相关标准规范确定不同破片质量mi(i＝1,2,...,k)系列阈值；

步骤9-2、依据公式[1]得到破片质量在mi到mj范围内的破片总质量为：

其中，mij为质量在mi到mj范围内的破片总质量；mi和mj为破片质量分组的下限和上限，mj>mi；m为战斗部各单元的弹体金属质量总和，即弹体的金属质量；；α为质量修正系数，其值根据模拟试验数据选取；

步骤9-3、各质量范围内的破片数量为：

其中，a和b是加权系数，a+b＝1，其值根据模拟试验数据选取；

步骤10、将所有单元的相同质量范围内的破片质量和数量相加，得到整个战斗部的破片质量与数量分布。

下面本实施例以130加榴弹破片质量与数量分布预测为例，具体描述自然破片战斗部破片质量与数量分布预测仿真计算方法。其中计算a、b值依据“15发小圆柱形模拟弹试验”经人工处理手工完成，130加榴弹破片质量与数量分布预测计算由我单位自主研发的《弹丸破片质量与数量分布预测计算软件》(著作权登记号：2019sr0905364)计算完成。

基于各种因素考量，本实施例中采用的弹体材料名称为“xx弹钢”，炸药名称为“xx炸药”；同时，破片质量分组范围采用我国现行破片质量分组标准，质量分组如下：mi＝0，0.2，1，4，8，12，16，20，30，50，100，200；mj＝0.2，1，4，8，12，16，20，30，50，100，200，500

计算方法流程参见图1，具体步骤如下：

步骤1、本实施例用130加榴弹的弹体材料为“xx弹钢”，其密度取铁的密度7.8克/厘米³，选用炸药为“xx炸药”，密度为1.67克/厘米³。按照上述弹体材料和炸药制作6发小圆柱形模拟弹，进行静爆试验后，按破片质量分组范围收集每发弹的破片质量与数量数据，并依据发明内容中的公式[1][2][3]，得到这种材料与炸药组合的cu与c/m关系为cu＝19.1+92.8(c/m)(即a＝19.1，b＝92.8)，该小圆柱形模拟弹试验结果见下表：

小模拟弹尺寸见下表：(尺寸单位mm，重量：kg)

步骤2、以弹丸头部端面为起点(即x＝0)，x表示到起点的距离(沿中心线)，根据130加榴弹弹丸纵向半剖图，确定各横截面的外半径r和内半径r与x的关系如表1。

表1各横截面半径与x的关系

根据几何特征，将弹丸分为10个单元，如图2所示，分割线到起点的距离x＝0，39，110，180，247，273，417，466，512，527，557。

至于步骤3到步骤10，则由《弹丸破片质量与数量分布预测计算软件》计算完成，具体步骤如下：

1)点击“导入计算指标”按钮，以电子表格文件的形式导入弹体密度、炸药密度、a、b值、弹体单元内外径等计算指标，如图3所示；

2)点击“预测计算”按钮，开始破片质量与数量分布计算，如图4所示；

3)点击“计算结果导出”按钮，以电子表格文件的形式导出破片质量与数量分布计算结果，如图5～图8所示。

本申请的方法由于是以破碎性相似关系为基础，故而简便易行，实用性强，同时，通过几何因素的修正，特别是弹底和无装药部分的修正以及质量修正系数α和加权系数a与b的引入，能大大提高预测结果精度，而且由于考虑了炸药、弹体结构、弹体材料等因素，能便于设计出具有理想破片杀伤效应的战斗部。