一种基于遥感数据的区域碳储量空间格局监测系统和方法与流程

本发明属于环境保护和城市规划技术领域，具体涉及一种基于遥感数据的区域碳储量空间格局监测系统和方法。

背景技术：

随着经济的快速发展，城市化建设已经蔓延到世界物质文化遗产地区的周边。政府间气候变化专门委员会(ipcc)评估报告认为，在过去的20年里至少有1/4的人为二氧化碳排放是由于土地利用变化造成的。由此，人类活动对碳循环的影响是气候变化研究的重要核心问题之一，在制定应对和缓解气候变暖的对策中，目前提出了通过经营土地来吸收co2的策略，因此准确确定土地利用变化对有机碳库的影响对科学认识陆地生态系统碳循环规律及制定缓解和应对全球气候变暖具有重要的理论和现实意义。

目前对碳储量观测的方式主要有三种：(1)基于站点的碳浓度观测；(2)基于卫星遥感平台的碳浓度观测；(3)基于大气碳循环模型的碳浓度模拟。基于地面定位观测的方式，可提供监测站点长时间序列、高精度、连续碳浓度观测数据，能够揭示碳浓度的年变化和季节变化趋势，对揭示碳浓度时空变化规律、大陆尺度源汇信息等提供了大量基础数据资料，但实际实施时对监测站点的密度要求高，投入成本高，不能大范围的同步观测，而基于卫星遥感平台正好弥补了这一缺点，卫星观测可以获得温室气体连续空间分布和变化，是监测温室气体分布的有效方法，观测资料具有稳定、长时间序列、广空间区域、空间三维监测的优点，帮助理解温室气体的源与汇以及大气、植被和土壤之间的碳循环过程。大气碳循环模型的碳浓度模拟不能准确反映中小尺度区域空间的碳储量变化，其结果会造成较大的误差。

技术实现要素：

本发明目的在于针对现有大范围区域碳储量的研究周期长的缺点，提供一种基于遥感数据的区域碳储量空间格局监测系统和方法，使用卫星遥感数据，采用降水量、植被覆盖率、地表温度、土地利用数据、灯光数据、dem数据和气象数据建立模型的方法来监测区域碳储量的时空变化。

本发明是通过以下技术方案实现的：

一种基于遥感数据的区域碳储量空间格局监测方法，所述方法包括：

步骤一、获取预设时间内遥感卫星观测的数据并进行预处理，分别得到降水量数据、modis数据、热红外影像数据、地表真实反射率数据、dem数据以及dmsp/ols夜光数据；其中，所述的降水量数据用于计算月累计降水数据；所述的modis数据通过ndvi计算法获取植被指数最大值；所述的热红外影像数据和地表真实反射率数据通过大气传输方程法获取地表温度；所述的地表真实反射率数据通过监督分类法获取土地利用分类图；所述的dem数据用于计算坡度、坡向和高程；所述的dmsp/ols夜光数据用于计算灯光密集区；

步骤二、获取预设时间内的气象站点数据和土壤检测数据，结合气象站点数据和土壤检测数据建立线性回归模型，使用土壤检测数据对线性回归模型进行精度评价；其中，所述的气象站点数据通过数据标准化转换生成月降水量、月气温值和月日照百分率的空间分布图；所述的土壤检测数据通过数据标准化分别抽取为模型样本和检验样本；

步骤三、基于步骤一得到的月累计降水数据、植被指数最大值、地表温度、坡度、坡向、高程以及灯光密集区与步骤二得到的月降水量、月气温值和月日照百分率的空间分布图建立土壤有机模型因子，并经过因子筛选和模型分析建立最佳模型线性组合；

步骤四、结合步骤二得到的精度评价结果与步骤三得到的最佳模型线性组合反演土壤有机含碳量，生成土壤有机碳空间密度分布图，得到土壤碳储量；

步骤五、基于步骤一得到的土地利用分类图统计土地分类面积和土地转移矩阵，结合casa模型得到植被碳储量；

步骤六、基于步骤四的土壤碳储量和步骤五的植被碳储量，确定区域碳储量空间格局，利用时间序列的相关性来确定土壤有机碳变化。

本发明进一步解决的技术方案是，步骤二具体如下：

建立多元线性总体回归方程：

y＝β0+β1x1+β2x2+…+βkxk(1)

求解回归系数的估计值：

使用检验样本对线性回归模型进行精度评价，测定方程的拟合程度：

对拟合程度进行调整：

由此评价回归方程的拟合程度；

式(1)中，β0为回归常数，β1,…βk称为回归系数；y为被解释变量；x1,x2,…xk是k个解释变量；

式(2)中，sse表示残差平方和，表示被解释变量估计值；

式(3)中，ssr表示回归平方和；sst表示离差平方和；sse表示残差平方和；表示被解释变量估计值；表示被解释变量平均值

式(4)中，r²表示拟合程度；(n-1)表示离差平方和的自由度；(n-k-1)表示残差平方和自由度。

本发明进一步解决的技术方案是，所述的数据标准化包括克里金插值法或泛克里金插值法。

本发明进一步解决的技术方案是，步骤三中，所述的土壤有机模型因子包括植被因子和地形因子；

其中，植被因子的具体计算包括：

dvi＝nir-red

式(5)中，nir表示卫星遥感影像的近红外数字量化值；red表示卫星遥感影像的红色波段的数字量化值；ndvi表示归一化植被指数；rvi表示比值植被指数；dvi表示差值植被指数；savi表示土壤调节植被指数；l为土壤调节系数，取值0.5；

地形因子直接由坡度、坡向和高程的数据表示。

本发明进一步解决的技术方案是，步骤四的具体如下：

建立土壤有机碳储量的多元线性回归模型：

式(6)中，为常数项，为回归系数，x1，x2，...，xn为影响土壤碳储量的自变量，δ为随机误差项。

本发明进一步解决的技术方案是，步骤五具体如下：

基于土地利用转移矩阵的计算公式为：

nc(i,j)＝nc(i)×10+nc(j),(j＞1)(1)

基于casa模型的植被净初级生产力计算公式为：

npp(x，t)＝apar(x，t)*ε(x，t)

ε＝t11×t22×w2×εmax(2)

由此得到植被碳储量；

式(1)中，nc(i,j)为i，j两年份的土地利用变化图；nc(i)为i年份遥感分类影像；nc(j)为j年份的遥感分类影像；

式(2)中，npp(x,t)表示像元x在t时间的植被净初级生产力(gc/m²·月)；apar(x,t)表示像元x在t时间吸收的光合有效辐射(mj/m²·月)；ε(x,t)表示像元x在t时间的实际光能利用率ε的值；tε1、tε2为温度胁迫系数；wε为水文胁迫系数；εmax为理想条件下光能利用率的最大值。

本发明进一步解决的技术方案是，基于式(2)的光合有效辐射apar的计算公式为：

apar(x，t)＝par(x，t)*fpar(x，t)(9)

式(9)中，par(x,t)表示t时间在像元x处太阳总辐射量，fpar(x,t)表示植被冠层对入射光合有效辐射的吸收比例；

式(10)中，ndvi表示归一化植被指数。

本发明进一步解决的技术方案是，步骤六中，所述土壤有机碳变化的计算公式为：

式(11)中，θslope为单个像元多时间的趋势斜率，ci为第i个时间碳储量值，n表示研究时间，单位为月、年，i表示研究开始的时间。

本发明还保护一种基于遥感数据的区域碳储量空间格局监测系统，包括遥感数据处理模块、实测数据处理模块和数据分析与输出模块；其中，所述的遥感数据处理模块和实测数据处理模块的输出端与数据分析与输出模块的输入端相连；

所述的遥感数据处理模块用于获取预设时间内遥感卫星观测的数据并进行预处理；

所述的实测数据处理模块用于获取预设时间内的气象站点数据和土壤检测数据并建立线性回归模型；

所述的数据分析与输出模块用于根据遥感数据处理层和实测数据处理层的数据确定植被碳储量和土壤碳储量，并利用时间序列的相关性来分析土壤有机碳变化。

本发明的有益效果为：

本发明所使用的数据源都是易获取的，都有较成熟的算法得到需要的产品数据，通过计算机编程实现自动化监测运行，耗费人力物力财力少，相比较其他模型准确反映用户需要的中小尺度区域空间的碳储量变化情况。

本发明结合了卫星遥感技术实现区域碳储量监测的全覆盖，避免了地面监测站数据插值带来的数据可性度低的缺点，充分发挥了遥感技术在碳储量变化监测方面的应用优势。

附图说明

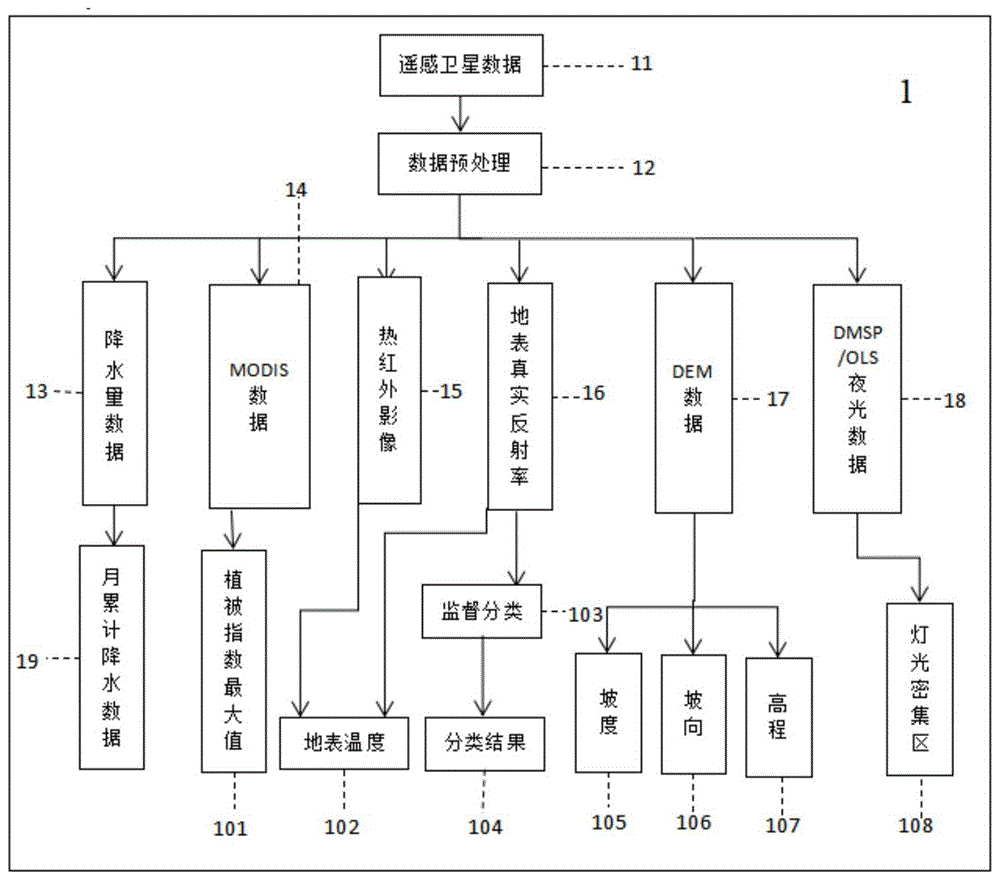
图1是本发明专利的遥感数据处理模块流程示意图。

图2是本发明专利的实测数据处理模块框图。

图3是本发明专利的数据分析与输出模块的流程图。

具体实施方式

下面结合附图和实施例对本发明的发明内容作进一步地说明。

一种基于遥感数据的区域碳储量空间格局监测系统，包括遥感数据处理模块、实测数据处理模块和数据分析与输出模块；其中，所述的遥感数据处理模块和实测数据处理模块的输出端与数据分析与输出模块的输入端相连；

所述的遥感数据处理模块用于获取预设时间内遥感卫星观测的数据并进行预处理；

所述的实测数据处理模块用于获取预设时间内的气象站点数据和土壤检测数据并建立线性回归模型；

所述的数据分析与输出模块用于根据遥感数据处理层和实测数据处理层的数据确定植碳储量和土壤碳储量，并利用时间序列的相关性来分析土壤有机碳变化。

参见图1-3，集到的遥感卫星数据进行数据预处理，包括辐射定标、大气校正、归一化植被指数(ndvi))计算、地表温度反演、夜光数据过滤和土地利用分类等操作；数据预处理的输出数据包括月累计降水量数据、modis地表反射率数据、陆地卫星landsat热红外数据和多光谱地表真实反射率数据、dem数据和灯光数据。数据预处理12的输出数据都具有相同的空间投影坐标系和删格行列数；

步骤一、获取预设时间内遥感卫星观测的数据并进行预处理，分别得到降水量数据、modis数据、热红外影像数据、地表真实反射率数据、dem数据以及dmsp/ols夜光数据；其中，所述的降水量数据用于计算月累计降水数据；所述的modis数据通过ndvi计算法获取植被指数最大值；所述的热红外影像数据和地表真实反射率数据通过大气传输方程法获取地表温度；所述的地表真实反射率数据通过监督分类法获取土地利用分类图；所述的dem数据用于计算坡度、坡向和高程；所述的dmsp/ols夜光数据用于计算灯光密集区；

首先通过modis数据计算植被指数(ndvi)，公式为：

ndvi＝(ρnir-ρred)/(ρnir+ρrsd)(12)

式(12)中，ρnir为近红外波段数据，ρred为红色波段数据。

然后利用热红外影像数据反演地表温度，用到地表真实反射率数据作为参考，具体方法为：

①大气透过率计算：

式(13)中：ω是大气水分含量(g*cm^-2)，α和β常量，分别α＝0.02和β＝0.6321；ρ0.9和ρ0.8分别是0.9和0.8波段的地面反射率；

②地表比辐射率的估算：

εsurface＝0.9625+0.0614fv-0.0461fv2

εbuilding＝0.9589+0.086fv-0.0671fv2(14)

式(14)中，εsurface和εbuilding分别代表自然表面像元和城镇像元的比辐射率；

③计算相同温度下黑体的辐射亮度值：

卫星传感器接收到的热红外辐射亮度值lλ由三部分组成：大气向上辐射亮度l↑；地面的真实辐射亮度经过大气层之后到达卫星传感器的能量；大气向下辐射到达地面后反射的能量。卫星传感器接收到的热红外辐射亮度值的表达式可写为(辐射传输方程)：

lλ＝[ε·b(ts)+(1-ε)l↓]·τ+l↑(15)

式(15)中，ε为地表辐射率，ts为地表真实温度，b(ts)为普朗克定律推到得到的黑体在ts的热辐射亮度，τ为大气在热红外波段的透过率；则温度为t的黑体在热红外波段的辐射亮度b(ts)为：

b(ts)＝[lλ-l↑-τ·(1-ε)l↓]/τ·ε(16)

式(16)中，τ为大气在热红外波段的透过率，l↑为大气向上辐射亮度w/(m²·sr·μm)，l↓为大气向下辐射亮辐射亮度w/(m²·sr·μm)。

④反演地表温度：

ts＝k2/ln(k1/b(ts)+1)(17)

式(17)中，k1和k2是常量。

接着，dem数据采用srtm_dem全球90米分辨率数据，分别通过以下公式计算坡度、坡向和高程。表示坡度最为常用的方法，用度数来表示坡度，利用反三角函数计算而得，其公式如下：α(坡度)＝arctan(垂直增量/水平增量)；坡向用于识别出从每个像元到其相邻像元方向上值的变化率最大的下坡方向。坡向可以被视为坡度方向。坡向是一个角度，将按照顺时针方向进行测量，角度范围介于0(正东)到360(仍是正东)之间，即完整的圆。不具有下坡方向的平坦区域将赋值为-1。

步骤二、获取预设时间内的气象站点数据和土壤检测数据，结合气象站点数据和土壤检测数据建立线性回归模型，使用土壤检测数据对线性回归模型进行精度评价；气象数据在国家气象科学数据共享服务平台上下载得到全国气象站点的温度和降水数据、日值及月值辐射数据及各个站点的经度，纬度，海拔高程；其中，所述的气象站点数据通过数据标准化转换生成月降水量、月气温值和月日照百分率的空间分布图；所述的土壤检测数据通过数据标准化分别抽取为模型样本和检验样本；

利用gis软件对气象数据进行克里金空间插值或泛克里金插值法，形成具有空间连续性的逐月气候变化数据；克里金插值法或泛克里金插值法计算方法为：

式(18)中，z0是点(x,y)的估计值，λi是权重系数；

具体步骤如下：

建立多元线性总体回归方程：

y＝β0+β1x1+β2x2+…+βkxk(19)

求解回归系数的估计值：

通过求解这一方程组便可分别得到β0,β1,…βk回归系数的估计值，当自变量个数较多时，计算十分复杂，必须依靠计算机独立完成。现在，利用spss，只要将数据输入，并指定因变量和相应的自变量，立刻就能得到结果。

使用检验样本对线性回归模型进行精度评价，对多元线性回归，也需要测定方程的拟合程度、检验回归方程和回归系数的显著性。测定方程的拟合程度：

同一元线性回归相类似，0≤r²≤1，r²越接近1，回归平面拟合程度越高，反之，r²越接近0，拟合程度越低。r²的平方根成为负相关系数(r)，也成为多重相关系数。它表示因变量y与所有自变量全体之间线性相关程度，实际反映的是样本数据与预测数据间的相关程度。判定系数r²的大小受到自变量x的个数k的影响。在实际回归分析中可以看到，随着自变量x个数的增加，回归平方和(ssr)增大，使r²增大。由于增加自变量个数引起的r²增大与拟合好坏无关，因此在自变量个数k不同的回归方程之间比较拟合程度时，r²不是一个合适的指标，必须加以修正或调整。

调整方法为：把残差平方和与总离差平方和的分子分母分别除以各自的自由度，变成均方差之比，以剔除自变量个数对拟合优度的影响。调整的r²为：

由上时可以看出，考虑的是平均的残差平方和，而不是残差平方和，因此，一般在线性回归分析中，越大越好；由此评价回归方程的拟合程度；

式(19)中，β0为回归常数，β1,…βk称为回归系数；y为被解释变量；x1,x2,…xk是k个解释变量；

式(20)中，sse表示残差平方和，表示被解释变量估计值；

式(21)中，ssr表示回归平方和；sst表示离差平方和；sse表示残差平方和；表示被解释变量估计值；y表示被解释变量平均值

式(22)中，r²表示拟合程度；(n-1)表示离差平方和的自由度；(n-k-1)表示残差平方和自由度。

步骤三、基于步骤一得到的月累计降水数据、植被指数最大值、地表温度、坡度、坡向、高程以及灯光密集区与步骤二得到的月降水量、月气温值和月日照百分率的空间分布图建立土壤有机模型因子，并经过因子筛选和模型分析建立最佳模型线性组合；

所述的土壤有机模型因子包括植被因子和地形因子；由植被因子采用归一化植被指数(ndvi)、比值植被指数(rvi)、差值植被指数(dvi)，土壤调节植被指数(savi)参与建立土壤有机碳储量模型。根据各波段反射率和各植被指数计算公式，计算4种植被指数，具体计算包括：

dvi＝nir-red

式(23)中，nir表示卫星遥感影像的近红外数字量化值；red表示卫星遥感影像的红色波段的数字量化值；ndvi表示归一化植被指数；rvi表示比值植被指数；dvi表示差值植被指数；savi表示土壤调节植被指数；l为土壤调节系数，取值0.5；

地形因子可利用dem数据计算得到高程、坡度数据。

步骤四、结合步骤二得到的精度评价结果与步骤三得到的最佳模型线性组合反演土壤有机含碳量，生成土壤有机碳空间密度分布图，得到土壤碳储量；在土壤碳储量估测研究中，模型的选择至关重要。常见的遥感估测模型主要有一元线性或非线性回归模型、多元回归模型，优选地，采用多元线性回归模型，利用两个或两个以上影响因素作为自变量与因变量建立最优模型来预测因变量。土壤有机碳储量的多元线性回归模型可以表示为：

式(24)中，为常数项，为回归系数，x1，x2，...，xn为影响土壤碳储量的自变量，δ为随机误差项。

选择自变量时应注意：自变量对因变量必须具有显著的线性相关性；自变量之间应具有一定的互斥性，即自变量之间的相关性不应高于自变量与因变量的相关性，以保证回归模型具有良好的预测效果和解释能力。多元回归模型的参数估计，在要求误差平方和最小的前提下，用最小二乘法求解。对于因变量较多的情况下，多元逐步回归可以决定自变量的去留，只保留对模型贡献较大的自变量。

步骤五、基于步骤一得到的土地利用分类图统计土地分类面积和土地转移矩阵，结合casa模型得到植被碳储量；

具体如下：

基于土地利用转移矩阵的计算公式为：

nc(i,j)＝nc(i)×10+nc(j),(j＞1)(25)

结合casa模型得到植被碳储。casa模型中植被净初级生产力(npp)的测算由植被吸收的光合有效辐射(apar)与光能转化率(ε)这凉个变量的乘积确定；基于casa模型的植被净初级生产力计算公式为：

npp(x，t)＝apar(x，t)*ε(x，t)

ε＝tε1×tε2×wε×εmax(26)

光能利用率ε是指植被通过光合作用，将所吸收的光合有效辐射转化为有机碳的效率。在理想条件下，某种植被的光能利用率可以达到最大值εmax，但实际情况是，植被的光能利用率主要受到温度、水分胁迫因子的影响，在大多数时候小于最大光能利用率；

由此得到植被碳储量；

式(25)中，nc(i,j)为i，j两年份的土地利用变化图；nc(i)为i年份遥感分类影像；nc(j)为j年份的遥感分类影像；

式(26)中，npp(x,t)表示像元x在t时间的植被净初级生产力(gc/m²·月)；apar(x,t)表示像元x在t时间吸收的光合有效辐射(mj/m²·月)；ε(x,t)表示像元x在t时间的实际光能利用率ε的值；tε1、tε2为温度胁迫系数；wε为水文胁迫系数；εmax为理想条件下光能利用率的最大值。

apar取决于太阳总辐射和植被对光合有效辐射的吸收比例，由于不同植被的生理特性会影响植被吸收的光合有效辐射，其对太阳辐射的吸收比例会产生不同的表现。公式如下：

apar(x，t)＝par(x，t)*fpar(x，t)(27)

其中，apar与植被类型和归一化植被指数(ndvi)关系密切，存在着一定的线性关系，这一关系可以通过植被ndvi的最大值和最小值来确定。

式(27)中，par(x,t)表示t时间在像元x处太阳总辐射量，fpar(x,t)表示植被冠层对入射光合有效辐射的吸收比例；

式(28)中，ndvi表示归一化植被指数。

在实际应用中，植被碳库由植物的地上生物量和地下生物量两部分决定的，地上生物量使用净初级生产力(npp)来计算，地下生物量采用地下与地上生物量比例系数来计算。

地上生物量与地下生物量的相关性关系可用下式表示：logy＝logb+αlogx；式中，y表示地上部分生长量，x表示地下部分生长量，α表示相关性的斜率，logb表示截距。

步骤六、基于步骤四的土壤碳储量和步骤五的植被碳储量，确定区域碳储量空间格局，利用时间序列的相关性来确定土壤有机碳变化；所述土壤有机碳变化的计算公式为：

式(29)中，θslope为单个像元多时间的趋势斜率，ci为第i个时间碳储量值，n表示研究时间，单位为月、年，i表示研究开始的时间。

dmsp/ols数据是用来确定土地利用分类结果中城市建成区的精确面积和分布，如若土地利用分类结果使用的是高分辨率卫星影像生成，则可以不使用dmsp/ols数据，具体可根据需要增加减少数据。

本发明使用的数据量和数据类型较多且计算量大，可以根据需要每个功能模块单独开发再组合，在上述实施方式的描述中，具体数据、算法、模块或者软件的运用可以在任何的一个或多个实施例或示例中以合适的方式结合。

需要补充的是，为了实现本发明的便利性，所使用的遥感卫星影像空间分辨率需要重采样到统一，方便后续空间分析和模型建立。

以上所述的仅是本发明的优选实施方式，应当指出，对于本领域的普通技术人员来说，在不脱离本发明创造构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。