一种生物样本高分辨率图像获取方法与流程

本发明属于生命科学医学成像技术领域，更具体地，涉及一种生物样本高分辨率图像获取方法。

背景技术：

在传统采样过程中，为了保证还原的信号不失真，采样频率不得低于信号最高频率的2倍，在这一理论下，巨大的采样数据量限制了信息获取的时间和效率。针对这一问题，有学者提出压缩感知法，其在信号具有稀疏性的条件下，可以在小于奈奎斯特采样的采样数下重建原始信号。这与最近广泛应用的机器学习相比，不需要任何训练数据和训练时间等限制条件，仅利用低分辨三维图像输入，就可以高效地进行高分辨图像高精度的重建。

现代的亚细胞分辨率的生物医学成像领域中，光片显微成像系统以通量高、分辨率较高等特点近几年飞速发展。其中贝塞尔光片系统通过扫描贝塞尔光束解决了传统光片成像系统大视野和高分辨率不能兼得的矛盾，得到厚度较薄且均匀的贝塞尔光片，同时具有大视场、高分辨率、各向同性等特点。但在实际生物成像应用中往往需要较高分辨率即高放大倍率用于观察生物样本，高放大倍率的成像需要更长的数据采集时间，更长时间的光漂白及光毒性。

因此，在现代的生物医学成像领域中，在较短的数据采集时间内，获得较高分辨率的数据，不仅可以减小光漂白光毒性对样本荧光的影响，还可以大大减小样本成像的时间成本和研究周期，是生物医学成像研究领域发展的广泛趋势。

技术实现要素：

本发明提供一种生物样本高分辨率图像获取方法，用以解决现有生物样本高分辨率图像获取中因需要采集多张低分辨率图像且计算过程需要不断对参数进行试值而存在高分辨率图像获取耗时的技术问题。

本发明解决上述技术问题的技术方案如下：一种生物样本高分辨率图像获取方法，包括：

s1、获取一张各维稀疏的低分辨率三维堆叠图像，所述三维堆叠图像为通过贝塞尔光片显微成像系统采集的生物样本的图像；

s2、基于所述三维堆叠图像的分辨率及实际所需的高分辨率，构建压缩感知法中三维的系统点扩散函数，并基于所述三维堆叠图像的稀疏度，由稀疏度与正则化因子成反比，对压缩感知法中的正则化因子取值；

s3、基于所述系统点扩散函数和所述正则化因子的取值，采用压缩感知法，将所述三维堆叠图像重建为高分辨率图像，完成高分辨率图像获取。

本发明的有益效果是：本发明利用贝塞尔光片显微成像系统采集低分辨率图像，贝塞尔光片显微成像系统具有高通量、高分辨率、各向同性的采集特点，可以利用贝塞尔光片在大视野中短时间内采集各维稀疏的低分辨图像，而由于压缩感知法具有在信号具有稀疏性条件下可以在小于奈奎斯特采样的采样数下重建原始信号得到高分辨率图像的特点，因此，贝塞尔光片显微成像系统和压缩感知法可以结合以进行高分辨图像重建，由于贝塞尔光片显微成像系统采集的图像为三维堆叠图像而非二维，对此本发明对压缩感知法进行优化改进，将压缩感知法中的系统点扩散函数进行三维重建，得到三维的系统点扩散函数，另外，在得到系统点扩散函数并采用压缩感知法进行迭代求解高分辨率图像之前，基于原始低分辨率三维堆叠图像的稀疏度首先确定压缩感知法中的正则化因子取值，基于该取值进行高分辨率图像构建，避免了在采用压缩感知法迭代求解高分辨率图像期间对正则化因子多次试值而存在耗时的问题，其中，在对正则化因子取值时通过稀疏度与正则化因子成反比进行拟合取值，充分考虑了稀疏度对求解过程的影响，提高求解效率和准确度。因此，本发明将具有高通量高分辨率等特点的贝塞尔光片照明显微成像系统与压缩感知结合，将高通量贝塞尔光片照明成像得到的单张三维堆叠图像作为输入，不需要多帧采集、高分辨耗时采集及任何训练等限制条件，避免了长时间采集图像对生物样本造成损失而存在图像失真等的问题，采用改进的压缩感知法进行高分辨率图像求解重建，能够实现高效、准确地生物样本高分辨率图像获取。

上述技术方案的基础上，本发明还可以做如下改进。

进一步，所述构建压缩感知法中三维的系统点扩散函数，具体为：

基于所述三维堆叠图像和实际所需高分辨率图像的分辨率，计算所述三维堆叠图像和所述实际所需高分辨率图像的像素尺寸；

基于所述贝塞尔光片显微成像系统的光学分辨率以及所有所述像素尺寸，计算三维高斯模糊函数中的σ值，以构建得到三维高斯模糊函数；

将所述三维高斯模糊函数与贝塞尔函数相乘，得到三维的系统点扩散函数。

本发明的进一步有益效果是：以三维高斯模糊函数为基础，以构建三维的系统点扩散函数，由于原始低分辨率三维堆叠图像由贝赛尔光片显微成像系统采集，因此采用压缩感知法时，将三维高斯模糊函数与贝塞尔函数相乘，得到用于对原始低分辨率三维堆叠图像进行高分辨率重建的三维系统点扩散函数，高效准确，可靠性高。

进一步，所述正则化因子λ的取值为：λ＝α·β；

其中，α＝2‖a^ty‖1，a为所述系统点扩散函数，y为低分辨率三维堆叠图像；β＝ke+b，且β和e成线性反比，e为y的熵，表征y的稀疏度，k、b为计算结果相对y而结构不变的条件下的拟合参数。

本发明的进一步有益效果是：正则化因子λ随输入图像的不同而改变，可以实现正则化因子随输入图像不同的自动计算。λ＝α·β，其中α由图像与a^’t卷积的最大值得到，确定λ的上限，根据数学证明，当λ>α时，将无法迭代收敛。β与输入图像的稀疏程度成反比关系，使用图像熵参数e对图像稀疏程度进行定量，即：β∝1/e，在0-1之间取值。若图像所拍摄样本结构复杂，信号密集且强弱差距较大，熵e较大，则λ较小，可以防止原图过多的限制条件导致过拟合；若图像所拍摄结构简单，信号稀疏或者强度分布较为均匀，熵e较小，则λ较大，对迭代过程进行更多的限制，防止伪影的出现。通过该种方式在迭代计算之前确定λ值，避免了多次试λ值导致耗时的问题，极大提高高分辨率图像的获取效率。

进一步，所述熵e的取值在1-3之间。

进一步，所述拟合参数k、b的取值：

若所述生物样本中的成像目标呈线状，取k＝-0.0841，b＝0.5199；

若所述生物样本中的成像目标呈圆点状，取k＝-0.3538，b＝1.8224。

进一步，所述s3包括：

基于压缩感知法中的l2范数最小化法，构建目标函数：求解通过对傅里叶变换，得到高分辨率图像x，求解约束条件为：其中，y为低分辨率三维堆叠图像，x为y对应的高分辨率图像，a为所述系统点扩散函数，λ为正则化因子，f为傅里叶变换矩阵；

基于所述正则化因子的取值，调整l2范数最小化法的参数，采用l2范数最小化法迭代求解，得到所述生物样本的高分辨率图像。

本发明的进一步有益效果是：由于低分辨率三维堆叠图像的稀疏度不同，对应正则化因子λ不同，由正则化因子自动调整l1范数优化算法的阈值、步长等参数。修改l1范数优化算法的阈值和步长参数，保障低强度信号的精准计算，以弥补三维生物样本成像中样本透明化对荧光猝灭的影响。

进一步，所述s2之前，所述方法还包括：

对所述三维堆叠图像分割，得到多块子三维堆叠图像，其中，每块子三维堆叠图像的内部信号结构疏密均匀；

则对各块子三维堆叠图像分别执行s2、s3，并对每块子三维堆叠图像对应的高分辨率图像进行拼接，得到所述生物样本的高分辨率图像。

本发明的进一步有益效果是：由于一次性处理较大的低分辨率三维堆叠图像，对于计算设备的要求较高，另外，由于同一张低分辨率三维堆叠图像不同部位的稀疏程度不同，则对于正则化因子取值会不同，因此，如果直接对一张低分辨率三维堆叠图像采用压缩感知计算，会造成计算成本高且精确度受限的问题，本发明先对低分辨率三维堆叠图像进行分割，对每张分割的图像进行正则化因子取值，后续进行拼接等处理得到大范围的分辨率较高的图像，实现更高效、准确地高分辨率图像重建。

进一步，所述对各块子三维堆叠图像分别执行s2、s3之前，所述方法还包括：对每块子三维堆叠图像进行傅里叶变换以稀疏化，得到多块稀疏三维堆叠图像，以对各块稀疏三维堆叠图像分别执行s2、s3。

本发明的进一步有益效果是：对原始低分辨率三维堆叠图像进行傅里叶变换，以对图像稀疏化，更加有利于采用压缩感知法进行高质量的高分辨率图像计算。

本发明还提供一种生物样本高分辨率图像，包括：对待成像生物样本，采用如上所述的任一种生物样本高分辨率图像获取方法获取得到该生物样本的高分辨图像。

本发明的有益效果是：本发明采用上述生物样本高分辨率图像获取方法得到待成像生物样本的高分辨率图像，图像相比较生物样本真实度高。

本发明还提供一种存储介质，所述存储介质中存储有指令，当计算机读取所述指令时，使所述计算机执行如上述任一种生物样本高分辨率图像获取方法。

附图说明

图1为本发明实施例提供的一种生物样本高分辨率图像获取方法的流程框图；

图2为本发明实施例提供的三维高斯模糊函数中σ值的计算示意图；

图3为本发明实施例提供的thy1-gfp鼠脑小脑神经横向面图像；

图4为本发明实施例提供的thy1-gfp鼠脑小脑神经轴向面图像。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

实施例一

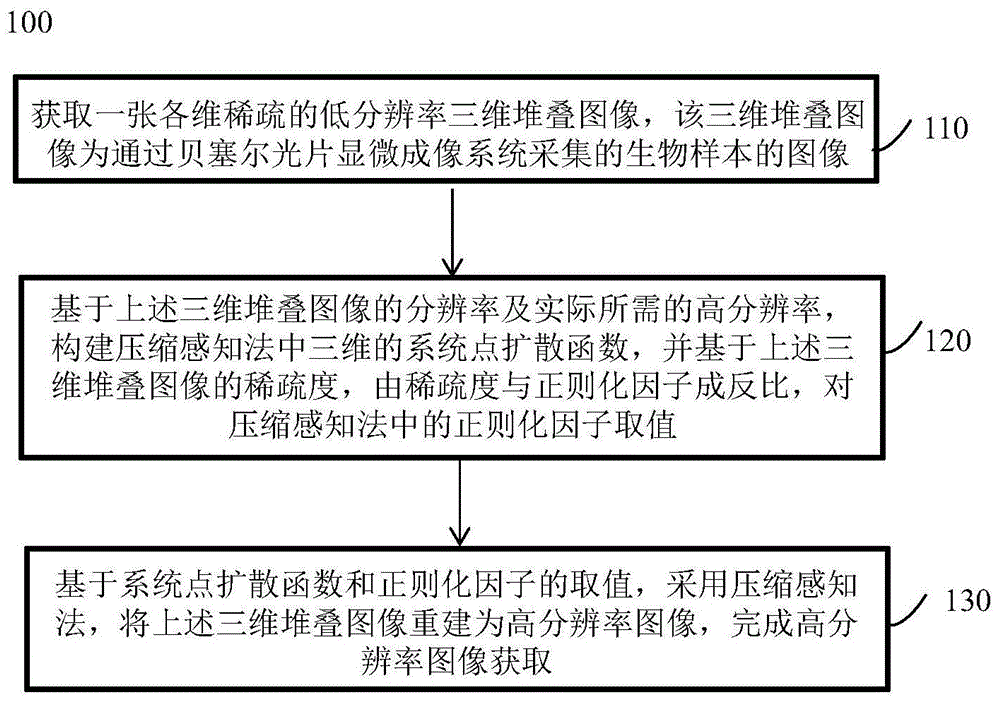
一种生物样本高分辨率图像获取方法100，如图1所示，包括：

步骤110、获取一张各维稀疏的低分辨率三维堆叠图像，该三维堆叠图像为通过贝塞尔光片显微成像系统采集的生物样本的图像；

步骤120、基于上述三维堆叠图像的分辨率及实际所需的高分辨率，构建压缩感知法中三维的系统点扩散函数，并基于上述三维堆叠图像的稀疏度，由稀疏度与正则化因子成反比，对压缩感知法中的正则化因子取值；

步骤130、基于系统点扩散函数和正则化因子的取值，采用压缩感知法，将上述三维堆叠图像重建为高分辨率图像，完成高分辨率图像获取。

压缩感知所需要处理的原始数据应该分布稀疏，分布稀疏的方法虽然可以是将数据从空间域经过傅里叶变换转换到频域的处理操作，但仍然需要样本本身结构不能太密集，因此本发明与贝塞尔光片显微成像系统结合，源数据本身在采样的时候，轴向用极薄的光片实现稀疏采样，因此同一层平面内信息仅包含被光片照射到的区域，与传统的共聚焦和宽场等成像方式相比，天然获得了更为稀疏的采样，符合压缩感知算法对于源数据的需求。另外，步骤110中，利用贝塞尔光片显微成像系统在较短时间内对生物样本进行低分辨图像的高通量采样，采集的图像比较稀疏，特别是在垂直于图像的z轴方向稀疏。

需要说明的是，贝塞尔光片显微成像系统对生物样本采集图像时，首先透明化处理生物组织，得到成像用的生物样本，采集的图像为模糊的低分辨率三维图像，而本方法目的即为基于该张低分辨率图像获得清晰的高分辨率三维图像。

优选的，上述构建压缩感知法中三维的系统点扩散函数，具体为：

基于三维堆叠图像和实际所需高分辨率图像的分辨率，计算上述三维堆叠图像和上述实际所需高分辨率图像的像素尺寸；

基于贝塞尔光片显微成像系统的光学分辨率以及所有像素尺寸，计算三维高斯模糊函数中的σ值，以构建得到以垂直图像方向为自变量方向的三维高斯模糊函数；

将三维高斯模糊函数与与其具有相同自变量方向的贝塞尔函数相乘，得到三维的系统点扩散函数。

a是系统的点扩散函数(psf)，表征显微镜对样本的降质过程，通常定义为：一个完美的无限小的点经过系统之后会变成一个具有具体半径的球。当样本中的每一个点都变成球，自然而然分辨率就会下降。

需要说明的是，将压缩感知(cs)扩展为三维的模型，即构建三维的系统点扩散函数，具体为：首先获取贝塞尔光片显微成像系统的光学分辨率，基于当前原始低分辨率三维堆叠图像的分辨率大小和实际所需的图像的高分辨率大小，计算得到两个图像的像素尺寸大小，基于光学分辨率和两个像素尺寸大小，可以计算得到三维高斯模糊函数中的σ值。

其中，将g(x)·b(x)＝a，其中，其中，σ的求法：例如，已知低分辨图像y是在3.2x下拍摄，希望构建的高分辨图像x能够达到12.6x的效果，根据查显微镜参数表可知，3.2x的光学分辨率12.6x单个像素大小是0.516um。则：

该式中的分子指模糊圆的半径，分母指该模糊圆被采样的像素大小。σ代表了三维的系统点扩散函数a能把该模糊圆扩的多大，单位是像素数，即：该模糊圆有0.5×1.103＝0.5515um大小，有1.1个像素大小。如图2所示，则σ＝4，占了四个像素。

优选的，上述正则化因子λ的取值为：λ＝α·β；

其中，α＝2‖a^ty‖1，a为三维的系统点扩散函数，y为上述低分辨率三维堆叠图像；β＝ke+b，且β和e成线性反比，e为y的熵，表征y的稀疏度，k、b为计算结果相对y而结构不变的条件下的拟合参数。

需要说明的是，计算原始低分辨三维堆叠图像的熵，该熵的大小表示该图像的稀疏程度。正则化因子λ随输入图像的不同而改变，可以实现正则化因子随输入图像不同的自动计算。λ＝α·β，其中α由图像与a^’t卷积的最大值得到，确定λ的上限，根据数学证明，当λ>α时，将无法迭代收敛。β与输入图像的稀疏程度成反比关系，使用图像熵参数e对图像稀疏程度进行定量，即：β∝1/e，在0-1之间取值。若图像所拍摄样本结构复杂，信号密集且强弱差距较大，熵e较大，则λ较小，可以防止原图过多的限制条件导致过拟合；若图像所拍摄结构简单，信号稀疏或者强度分布较为均匀，熵e较小，则λ较大，对迭代过程进行更多的限制，防止伪影的出现。通过该种方式在迭代计算之前确定λ值，避免了多次试λ值导致耗时的问题，极大提高高分辨率图像的获取效率。

优选的，上述熵e的取值在1-3之间。

优选的，上述拟合参数k、b的取值：

若上述低分辨率三维堆叠图像y是一堆模糊的线，取k＝-0.0841，b＝0.5199；

若上述低分辨率三维堆叠图像y是一堆模糊的点，取k＝-0.3538，b＝1.8224。

以当前迭代计算(相对于初始y)不多结构也不少结构，拟合得到各参数数据，具体拟合方式可为：确定图像的熵e，试出正则化因子λ，进而拟合k、b，进一步算出β，并经过多次重建，总结出β在0-1之间。

优选的，步骤130包括：

基于压缩感知法中的l2范数最小化法，构建目标函数：求解通过对傅里叶变换，得到高分辨率图像x，求解约束条件为：其中，y为低分辨率三维堆叠图像，x为y对应的高分辨率图像，a为所述系统点扩散函数，λ为正则化因子，f为傅里叶变换矩阵；

基于正则化因子的取值，调整l2范数最小化法的参数，采用l2范数最小化法迭代求解，得到生物样本的高分辨率图像。

需要说明的是，当期待高分辨率图像x在变换域内稀疏时，在趋近于零的限制下，通过解稀疏变换的l1范数最小化的方式，求解出经过傅里叶逆变换，高精准度地恢复高分辨率图像x，即：

设目标函数：将f(x)最小化，得到最优解：

优选的，步骤120之前，方法100还包括：

对上述低分辨率三维堆叠图像分割，得到多块子三维堆叠图像，其中，每块子三维堆叠图像的内部信号结构疏密均匀；

则对各块子三维堆叠图像分别执行步骤120、130，并对每块子三维堆叠图像对应的高分辨率图像进行拼接，得到上述生物样本的高分辨率图像。

由于一次性处理较大的低分辨率三维堆叠图像，对于计算设备的要求较高，另外，由于同一张低分辨率三维堆叠图像不同部位的稀疏程度不同，则对于正则化因子取值会不同，因此，如果直接对一张低分辨率三维堆叠图像采用压缩感知计算，会造成计算成本高且精确度受限的问题，本发明先对低分辨率三维堆叠图像进行分割，对每张分割的图像进行正则化因子取值，后续进行拼接等处理得到大范围的分辨率较高的图像，实现更高效、准确地高分辨率图像重建。

优选的，上述对各块子三维堆叠图像分别执行步骤120、130之前，方法100还包括：对每块子三维堆叠图像进行傅里叶变换以稀疏化，得到多块稀疏三维堆叠图像，以对各块稀疏三维堆叠图像分别执行步骤120、130。

由于生物样本本身结构不均匀，对整个图像进行分割，将分割后的每个图像进行傅里叶变换到空间域，将数据稀疏化。具体的，对低分辨信号y进行稀疏变换其中f为傅里叶变换矩阵，为y在傅里叶稀疏域f内的等价表示(将数据进行傅里叶变换到空间域，将数据稀疏化)。

为了更好的说明本实施例方法的效果，例如，如图3所示的thy1-gfp鼠脑小脑神经横向面，左图为3.2倍低分辨率图像；中间的图像为采用实施例一所述方法后横向分辨率提升4倍后重建图像；右图为采集的12.6倍高分辨图像；如图4所示的thy1-gfp鼠脑小脑神经轴向面图像，上图为3.2倍低分辨图像；中间图为采用实施例一所述方法后横向分辨率提升2倍后重建图像；下图为12.6倍高分辨图像。

从图中可以看出，采用本实施例方法获取的高分辨率图像相比较原始低分辨率图像，清晰度明显提高，且相比较直接采集高分辨率图像相比，重建的高分辨率图像清晰度更高。

因此，本实施例方法以高通量的贝塞尔光片显微成像系统与压缩感知重建算法的结合，可以利用贝塞尔光片在大视野中短时间内采集低分辨数据，再由压缩感知进行高分辨重建。在有效保证分辨率足够的情况下，实现采集时间更短、采集数据量更小、光漂白光毒性的影响更小等优点的样本图像数据采集，并实现原始数据更高分辨率的图像重建，扩大了光片显微成像系统在生物医学成像领域中的应用范围，为生物医学成像领域提供了一种仅利用单张低分辨三维图像输入，不需要多帧采集以及任何训练等限制条件，高效地进行高分辨图像重建的方法。

实施例二

一种生物样本高分辨率图像，对待成像生物样本，采用如实施例一所述的任一种生物样本高分辨率图像获取方法获取得到该生物样本的高分辨图像。

相关技术方案同实施例一，在此不再赘述。

实施例三

一种存储介质，所述存储介质中存储有指令，当计算机读取所述指令时，使所述计算机执行上述如实施例一所述的任一种生物样本高分辨率图像获取方法。

相关技术方案同实施例一，在此不再赘述。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。